Файл: Электронное пособие Scilab.pdf

16 

Таблица1.1.2-1 

Константа 

Назначение 

%i 

Мнимая единица. 

%pi 

Число π=3.1415926… 

%e 

Числоe=2.141592653589793 

%eps 

Условный ноль %eps=2.220Е-16 

%inf 

Значение машинной бесконечности. 

ans 

Переменная,хранящая результат последней операции. 

%NaN 

Указание  на  нечисловой  характер  данных  (Not-a-
Number) 

Переменные

  –  это  объекты  имеющие  имена.  Они  способны 

хранить  некоторые,  разные  по  значению,  данные.  В  зависимости  от  этих 
данных, переменные могут быть числовыми или  символьными, векторными 
или  матричными.  Имена  переменных  (идентификаторы)  задаются  по 
следующим правилам: 

•  имя переменной может состоять из символов латинского алфавита, 

знака подчёркивания и цифр, но начинаться обязательно с буквы;  

•  в имени переменной различаются прописные и строчные буквы;  
•  в имя переменной не входит пробел; 

•  имя  переменной  не  должно  совпадать  с  именами  других 

переменных, функций, то есть должно быть уникальны; 

•  желательно  использовать  содержательные  имена  для  обозначения 

переменных. 
 

Обратите  внимание,  что  переменные  и  их  типы  заранее  не 

декларируются  (не  объявляются).  Они  объявляются  выражением, 
значение которого, после вычисления, присваивается переменной. 

 
В 

оперативной 

памяти 

компьютера 

переменные 

занимают 

определенное  количество  байтов.  Как  известно  эта  область  называется 
Обозреватель переменных. 

Операция 

присваивания 

используется 

для 

задания 

переменным определенных значений и обозначается знаком равенства =: 

Имя переменной = Выражение 
Имя переменной = Выражение; 
 

17 

Арифметические  операции 

в  системе  Scilab  можно 

проводить  вычисления,  как  с  вещественными,  так  и  с  комплексными 
числами. Полный список арифметические операции приведен в табл. 1.1.2-2. 

 
Следует обратить внимание, что в  математических  выражениях 

с операциями +,  -,  * ,^,  /, \  участвуют как вектора так и матрицы. 

Первые  восемь  операций  действуют  в  соответствии  с  правилами 

линейной  алгебры,  т.е.  с  правилами  операций  над  векторами  и 
матрицами. 

Последние  четыре  операции,  так  называемые  операции  с  точкой, 

осуществляют поэлементные операции над массивами. 
 

Таблица 1.1.2-2 

Названиефункции 

Операция  Синтаксис 

Плюс 

+ 

M1+M2 

Унарный плюс 

+ 

+M 

Минус 

- 

М1-M2 

Унарный минус 

- 

-М 

Матричное умножение 

* 

M1*M2 

Поэлементное 

умножение 

массивов 

.* 

A1.*A2 

Возведение матрицы в степень 

^ 

М^х 

Поэлементное 

возведение 

массива в степень 

.^ 

A.^x 

Обратное 

(справа 

налево) 

деление матриц 

\ 

M1\M2 

Деление матриц слева направо 

/ 

M1/M2 

Поэлементное  деление  массивов 
справа налево 

.\ 

A1.\A2 

Поэлементное  деление  массивов 
слева направо 

./ 

A1./A2 

 
Подробнее  операции  над  векторами  и  матрицами  рассмотрены  в  

Теме 1.2. 

Приоритет  исполнения 

математических  операций  в  Scilab 

аналогичен  приоритету  в  языках  программирования  высокого  уровня: 
возведения  в  степень,  умножения  и  деления,  сложения  и  вычитания.  Для 
изменения приоритета в математических выражениях используются круглые 
скобки.  

Функции

 – это имеющие уникальные имена объекты, выполняющие 

определенные  преобразования  своих  аргументов  (параметров)  и  при  этом 
возвращающие  результаты  этих  преобразований.  Возврат  результата–

18 

отличительная  черта  функций.  Функции  могут  быть  встроенными 
(внутренними)  функциями  системы  Scilab,  функциями  пользователя, 
которые могут дополнять 

встроенные функции и описанные конкретным 

пользователем для своих нужд, внешними функциями, или sci-функциями. 

 
Scilab  обладает  большим  набором  элементарных  встроенных 

(библиотечных)  функций,  в  том  числе  математических.  Встроенные 
функции  хранятся  в  откомпилированном  виде  в  ядре  системы  Scilab. 
Некоторые из них приведены в табл. 1.1.2-3. 

Таблица 1.1.2-3 

Тригонометрические функции (аргумент задается в радианах)

sin(), cos(), tan(), cotg() 

Синус, косинус, тангенс и котангенс 

sec(), csc() 

Секанс, косеканс 

Обратные тригонометрические функции (результат в радианах)

asin(),acos(),atan(), 
atan2(), acot() 

Арксинус, арккосинус, арктангенс и арккотангенс 

asec(), acsc()  

Арксеканс, арккосеканс 

Алгебраические и арифметические функции

abs(), sign() 

Модуль и знак числа 

exp() 

Экспоненциальная функция 

log(), log2(), log10() 

Логарифм натуральный, по основанию 2 и 10 

sqrt() 

Квадратный корень 

fix() 

Целая часть числа 

floor() 

Округление до ближайшего целого значения, 
которое не превышает аргумент 

sign() 

Знак числа 

factorial() 

Вычисление факториала числа 

Гиперболические функции

sinh(), cosh(), tanh(), coth()  

Гиперболические синус, косинус, тангенс и 
котангенс 

sech(), csch()  

Гиперболические секанс и косеканс 

asinh(), acosh(), atanh(), 
acoth()  

Гиперболические арксинус,  
арккосинус, арктангенс и арккотангенс; 

Функции для работы с комплексными числами

conj() 

Комплексно-сопряжённое число 

imag() 

Мнимая часть числа 

real() 

Вещественная часть числа 

gcd(), lcm() 

Наибольший и наименьший общий делитель 

angle() 

P = angle(Z) возвращает фазу угла в радианах. 
Для комплексного Z, модуль R и фаза угла P 
Связаны следующим образом: 
R = abs(Z)    theta = angle(Z)   Z = R.*exp(i*theta) 

isreal() 

Возвращает логическую 1, если число 
действительное и 0 – если комплексное. 

 
  Система Scilab  предоставляет пользователю средства для создания и 

использования  своих  собственных  функций  –  так  называемых  функций 
пользователя. О создании и использовании функций в виде m-файлов речь 
пойдет в главе 1.1.3. 

19 

Рассмотрим несколько примеров рис. 1.1.2-1. 
 

Рис. 1.1.2-1. Примеры использования встроенных функций Scilab 

 
Кроме  математических  выражений  в  Scilab  используются  логические 

выражения. 

Логические  выражения

в  Scilab  строятся  на  основе 

математических  выражений,  операций  отношения  и  соответствующим  им 
функций,  логических  операций  и  функций,  а  также  круглых  скобок. 
Результатом  логического  выражения  является  значение  равное  T,  если 
выражение Истинно (True), или значение F в противном случае – выражение 
Ложно  (False).  Если  операнды  –  действительные  числа,  то  использование 
операций аналогично. 

Операции отношения 

и соответствующие им функции служат 

для  сравнения  двух  величин,  векторов  и  матриц.  Список  операций 
отношений приведен в табл. 1.1.2-4. 

Таблица 1.1.2-4 

Функция 

Операция 

Описание 

Пример 

eg() 

== 

Равно 

x==y;      eg(x,y); 

ne() 

~= 

Не равно 

x~=y;      ne(x,y); 

lt() 

< 

Меньше чем 

x<y;         lt(x, y); 

gt() 

> 

Больше чем 

x>y;         gt(x,y); 

le() 

<= 

Меньше или равно 

x<=y;       le|(x,y); 

ge() 

>= 

Больше илиравно 

x>=y;       ge(x,y); 

20 

Операции  отношений  выполняют  поэлементное  сравнение  векторов 

или  матриц  одинакового  размера  и  возвращает  значение  равное  1,  если 
элементы идентичны, и значение 0 в противном случае.  

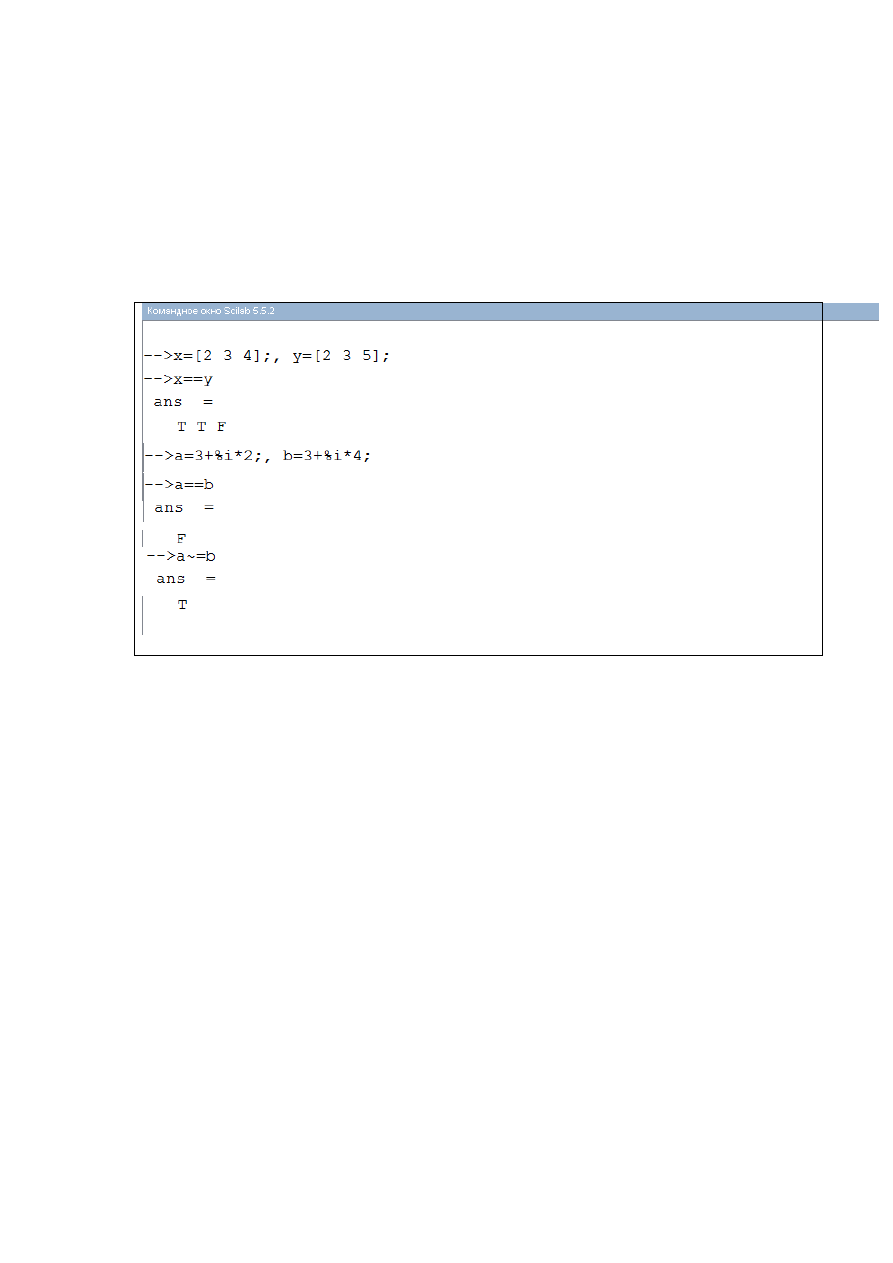
Следует  отметить,  что  операции  <,  <=,  >,  >=  при  комплексных 

операндах  используются  для  сравнения  только  действительные  части 
операндов – мнимые отбрасываются. В то же время операции  == и  ~= 
ведут  сравнения  с  учетом  как  действительной,    так  и  мнимой  частью 
операндов (рис. 1.1.2-2). 

Рис. 1.1.2-2. Примеры операций отношения над векторами и  

комплексными числами 

Операции 

отношения 

обычно 

применяются 

в 

логических 

выражениях, которые являются условиями операторов if, for, while, switchи 
служат  для  изменения  последовательности  выполнения  операторов 
программы  Scilab.  Использование  этих  операторов  подробно  рассмотрено  в 
Теме 1.3. 
 

При  вычислении  выражений  операции  отношений  имеют  более 

низкий  приоритет  чем  арифметические,  но  более  высокий  чем  логические 
операции. 
 

Логические операции 

и соответствующие им функции служат 

для  поэлементных  логических  операций  над  элементами  одинаковых  по 
размеру  массивов.  Список  логических  операций  отношений  приведен  в  
табл. 1.1.2-5.