ВУЗ: Московский технический университет связи и информатики
Категория: Учебное пособие
Дисциплина: Информатика
Добавлен: 15.11.2018
Просмотров: 12827
Скачиваний: 228
21
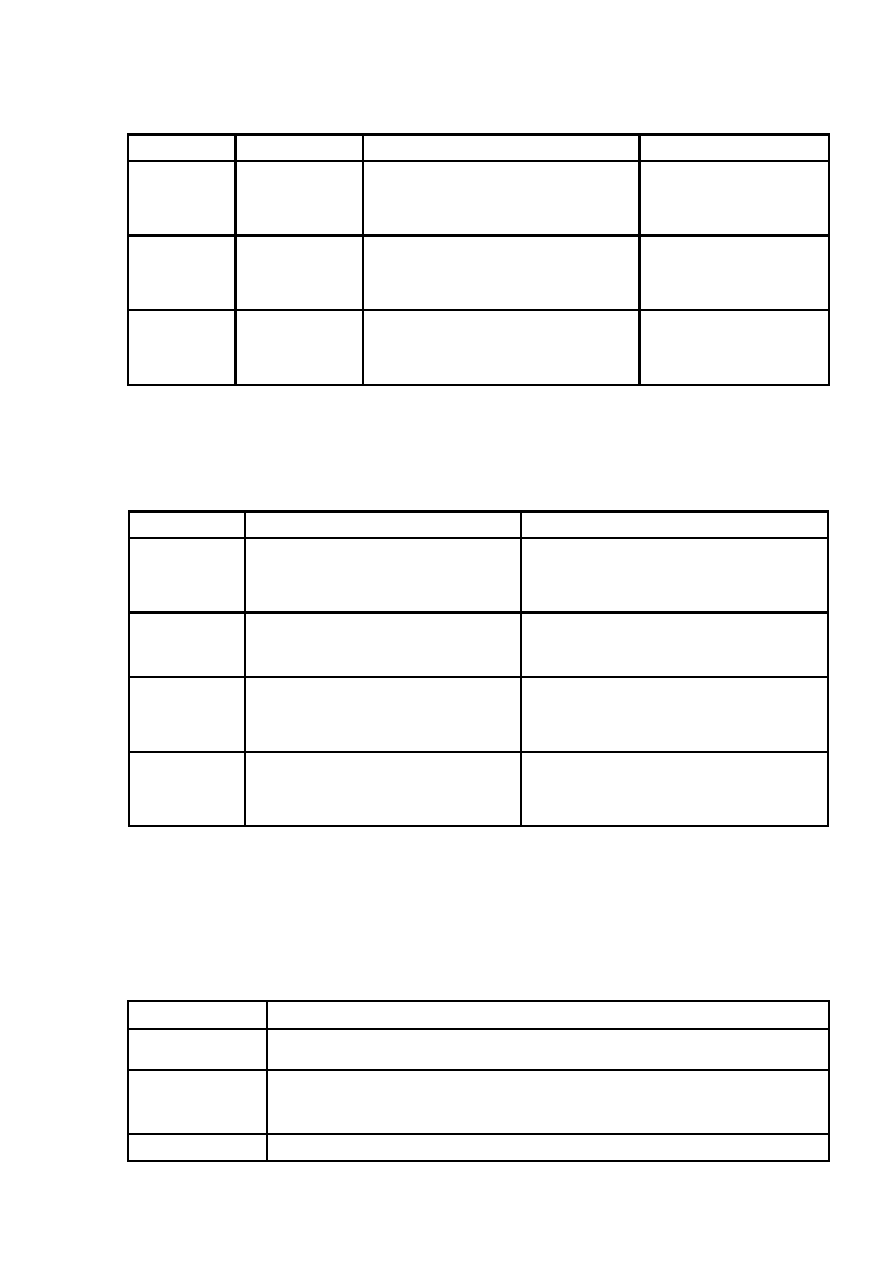
Таблица 1.1.2-5
Функция Операция
Описание
Пример
and()
&
Логическое умножение (И)
>>x&y
ans =
TFF
or()
!
Логическое сложение (ИЛИ) >>or(x,y)
ans =
TTT
not()
~
Логическое НЕ
>> ~x
ans =
FTT
Логические функции дополняют
логические операции и
представлены в табл. 1.1.2-6 где в примерах используются вектора x=[1 0 0] и
y=[111].
Таблица 1.1.2-6
Функция
Описание
Пример
xor ()
Исключающее ИЛИ
>>xor(x,y)
ans =
FTT
all()
Верно, если все элементы
вектора не равны 0
>>all(x)
ans =
F
any()
Верно, если все элементы
вектора равны 0
>>any(x)
ans =
T
find()
Нахождение
ненулевых
элементов в векторах
>>find(x)
ans =
T
Специальные операции
реализуются с помощью специальных
символов (табл. 1.1.2-7). Они предназначены для создания самых
разнообразных объектов входного языка системы Scilab и придания им
различных форм.
Таблица 1.1.2-7
Обозначение
Название
:
Двоеточие – формирование под векторами и подматриц.
( )
Круглые скобки используются для задания порядка выполнения
операций в выражениях, указания последовательности аргументов
функции и указания индексов элемента вектора или матрицы.
[ ]
Квадратные скобки –формирование векторов и матриц.

22
{ }
Фигурные скобки –формирование массивов ячеек
.
.
Десятичная точка используется для отделения дробной части чисел
от целой.
..
Две точки подряд указывают на родительский каталог – переход по
дереву каталогов на один уровень вверх.
...
Три точки подряд указывают на продолжение строки.
,
Запятая – разделитель элементов.
;
Точка с запятой используется внутри круглых скобок для разделения
строк матриц, а также в конце операторов для запрета вывода на экран
результата вычислений.
%
Знак процента – начало комментария.
=
Символ
равно используется
для
присваивания
(операция
присваивания) значений в выражениях.
'
текст'
Одиночные кавычки(апострофы),внутри которых заключен
текст, интерпретируемый как вектор символов с компонентами,
являющимися символами. Кавычка внутри строки задается двумя
кавычками
'
Кавычка
(апостроф)–транспонирование
матриц
(А').
Для
комплексных матриц транспонирование дополняется комплексным
сопряжением, т.е. строки транспонированной матрицы соответствуют
столбцам исходной матрицы.
.
'
Точка с кавычкой (точкам с апострофом)–транспонирование
массива (А.') Для комплексных массивов операция сопряжения не
выполняется.
[,]
Квадратные скобки с перечислением внутри их элементов через
запятую –горизонтальная конкатенация– объединение матриц А и
В[А,В].
[;]
Квадратные скобки с перечислением внутри их элементов через
точкой с запятой – вертикальная конкатенация– объединение матриц
А и В[А;В].
Функции пользователя –
это функции, создаваемые
пользователем системы, которые значительно облегчают работу за счет
частого использования в математических выражениях, получении таблиц
значений функций и построении графиков.
Как правило, функции создаются для обработки множества значений
аргументов, поэтому при описании их математических выражений
используются операции с точкой. Функцию можно создать внутри
командного окна. Начинается она со слова function, а заканчивается словом
endfunction. Первая строка имеет следующий формат:
function [y1,…,yn]=Имя(x1,…xk),
где yi – выходные аргументы и xi–входные аргументы.
Функция может иметь несколько аргументов, тогда они перечисляются
через запятую. Имя функции формируется аналогично имени переменной и
должно быть уникально.
23
Создание функции с использованием команды deff имеет следующий
формат:
deff(‘[w]=fun(x1,…,xk)’,[‘оператор1’;…’ операторk’])
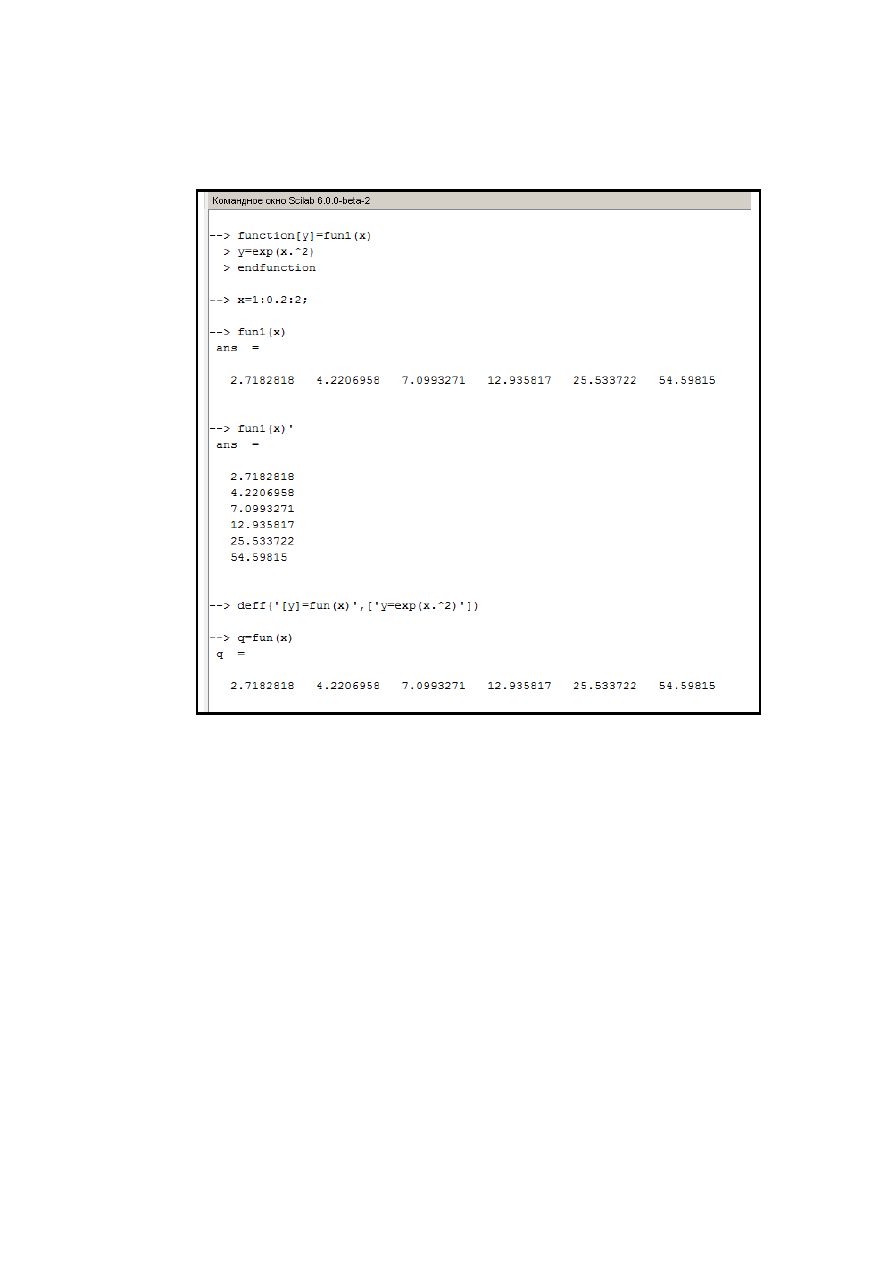
Рис.1.1.2-3. Примеры описания и использования функции
В примере (рис. 1.1.2-3) описания функция
2
)
(
x
e
x
y
и получения ее
значений для множества значений аргумента xс использованием описанных
выше средств. Традиционное обращение к функции выводит значения
функции в строку, а добавление символа апостроф (') – в столбец.
Наряду с рассмотренными выше функциями пользователя в Scilab
имеется возможность создания функций (или некоторой последовательности
вычислений) в виде sci-файлов, которые можно сохранять и использовать в
других сеансах работы. Подробнее материал о создании и работе с sci-
файлами, а также о средствах программирования в среде Scilab, изложен в
Теме 3.1.
Символьная константа
– это последовательность символов,
заключенных в одиночные апострофы. Например, 'Информатика'
Комментарии
в Scilab определяются с помощью символов//.
Например,
% Это комментарий

24
1.1.3. Лабораторная работа по теме
«Элементы рабочей среда Scilab
и простейшие вычисления»
1.
Вопросы, подлежащие изучению
1) Элементы основного окна Scilab.
2) Окно панели Командного окна.
3) Установка свойств среды системы Scilab.
4) Основные объекты системы Scilab.
5) Правила записи и вычисления арифметических выражений.
6) Работа с функциями пользователя, заданными в окне Командное окно.
7) Назначение окон Обозреватель переменных и Журнал команд.
2.
Общее задание
1)
Изучите материал Темы 1.1 (п.п. 1.1.1 – 1.1.2).
2)
Выполните команду clear all для очистки Рабочей среды.
3)
Выберите вариант задания формул из табл. 1.1.3-1.
4)
Задайте переменным x и yдопустимые числовые значения.
5)
Проанализируйте информацию, возникшую в окне Обозреватель
переменных.
6)
Введите формулу для вычислений арифметического выражения и
получите результат.
7)
Измените значения исходных данных.
8)
Измените формат вывода результата, выполнив команду
format long, и произведите перерасчет значения выражения.
9)
Верните формат вывода данных short.
10) Представьте арифметическое выражение в виде правой части
функции f(x).
11) Опишите функцию f(x) с помощью оператора deff числовое
значение при новом значении переменной х.
12) Опишите функцию f1(x) с помощью оператора function.
13) Измените значение переменнойy, вычислите значения
выраженияbи функции f1(x).
14) Объясните, почему изменение значенияyпривело к изменению
значении b, но не повлияло на значение функции.
15) Задайте диапазон изменения аргумента функции с шагом,
позволяющим получить таблицу значений функции f(x) и f1(x)для
заданных значений аргумента (порядка 8-10 точек), выведете
значения функции f(х) в выбранном интервале вначале в строку, а
затем в столбец.

25
16) Выполните команду who и проанализируйте выведенную
информацию о данных.
17) Установите путь к папке, находящейся на вашей флешь-карте, для
сохранения содержимого Командного окна.
18) Создайте файл в текущей папке.
19) Выделите в окне Командного окна с использованием команд
diary(‘имя_файла’) и diary(0)область сохранения.
20) Сохраните текст рабочего окна на внешнем носителе
21) Предоставьте результаты работы преподавателю, ответьте на
поставленные вопросы.
22) Выполните команду clear all для очистки Рабочей среды.
23) Оформите отчет по выполненной работе.
3.
Варианты индивидуальных заданий
Таблица 1.1.3-1
№
Формулы для
вычислений
№
Формулы для
вычислений
1.
2
π sin (x 8y)
t
cos
7
2,7(x
π)
16.
2
2
lg x
sin xy
b
0,8 ln(1 x)
2.
xy 2
2
(1 e )
d
0,7lg 1 x
17.
4
x
3
2y
2
e
| sin y |
d 10
2,5 cos x
3.
xy
sin x
h
1 y ln x
18.
3
2
π
ln x
3
f
x sin y
3y
x
4.
2
2
2
2
(yx
1)
с
(cos y sin x )
2
19.
2
2
y
208 lg x
x
h
x
y
e
5.
2
3
x
y
b
sin(tg x)
0,2x
20.
2
x
5
2xy
a
10
lg 0.8x e
6.
xy
2
xe
8 sin x
d
x(x
y)(3x
y)
21.
y
x sin y
x
b
1
1
е
7.
2
π
x y
z
2x
2
0,75tg x
y
22.
2
3
sin x
c
x lg x
6
yx
8.
2
2
3
xy
x
2,5 10 y
d
0.5
2sin xy
23.
2
3
14 sin x
y
a
0.92 cos x
9.
3
lg(x
y)
f
5,2
0.5
1
x
0,45 sin(x
8y)
24.
2
x -xy
a
0.7sinln|x|
10.
5
x( y 1,2)
3
a
0,8 10 (xe
yx)
25.
2
2
y
2.71x
cos y
c
tg(x ) e