Файл: Электронное пособие Scilab.pdf

36 

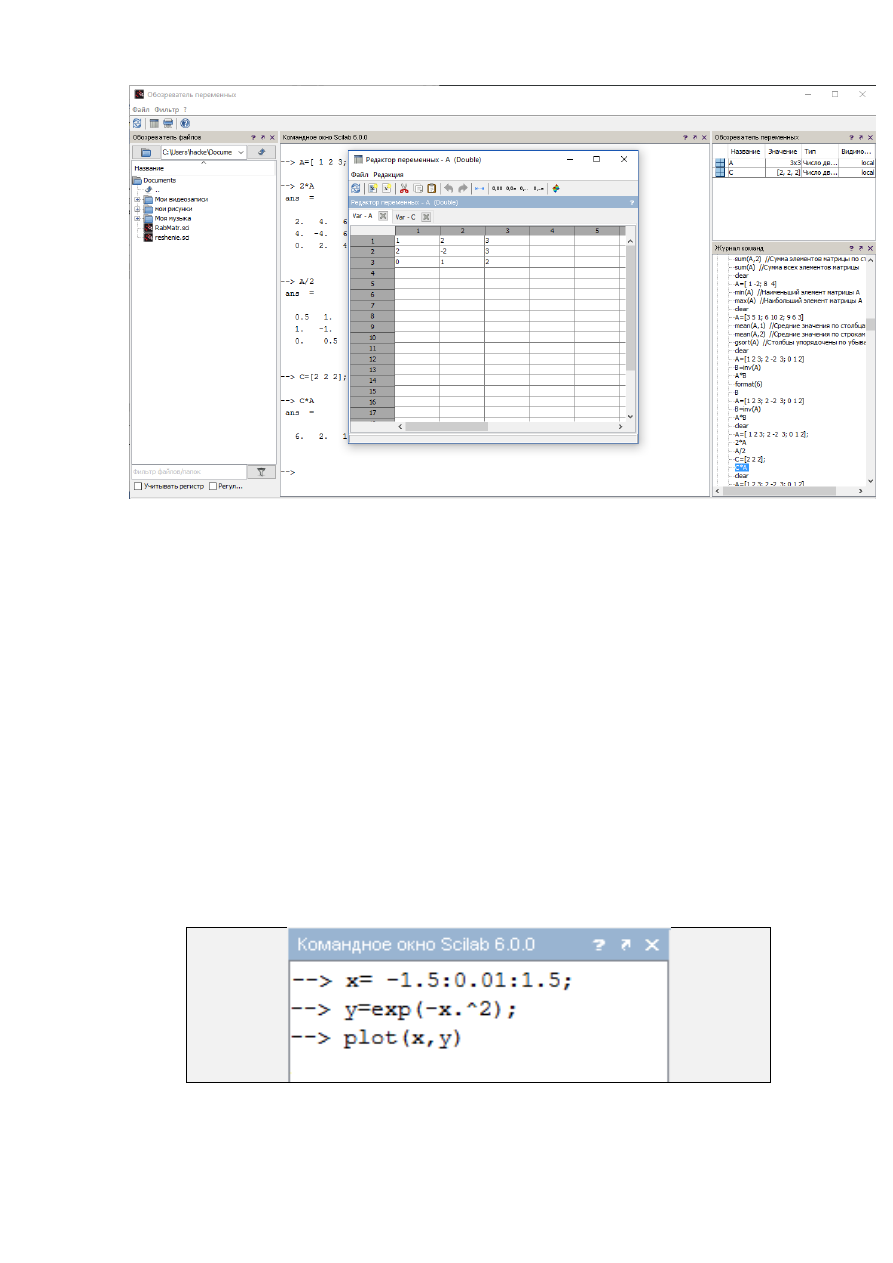
Рис. 1.2.1-13. Окно Рабочей среды с активной инструментальной панелью 

Редактором переменных 

1.2.2.  Построение графиков и визуализация вычислений 

в системе Scilab 

Самый  простой  способ  для  построения  графика  функции  одной 

переменной  y=f(x),  это  предварительное  формирование  двух  векторов 
одинаковой длины: вектор значений аргументов x и вектор соответствующих 
им значений функции у, а затем выполнение команды plot(x, y). Выполнение 
команды  plot(x,  y)открывает  графическое  окно  и  отображает  в  нем  график 
функции  y(x).  

Рассмотрим пример построения графика функции

2

x

e

y





  на отрезке 

[-1.5;1.5] (рис.1.2.2-1). 

Рис. 1.2.2-1. Команды построения графика функции 

2

x

e

y





37 

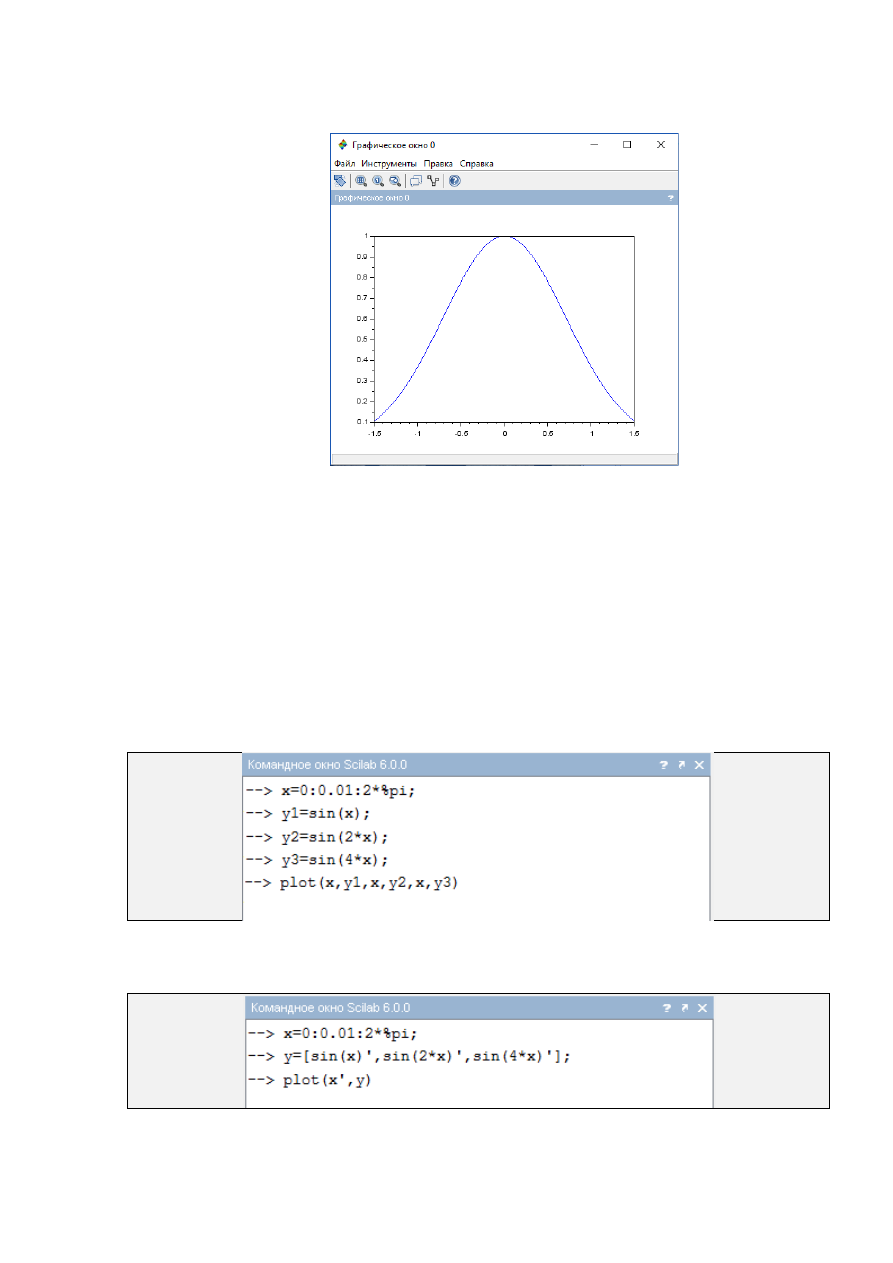
В  результате  выполнения  команды  plot(x,y)  появляется  графическое 

окно с номером  (рис. 1.2.2-2). 

Рис. 1.2.2-2. Графическое окно с изображением графика функции 

2

x

e

y





 
Переход  между  окнами  (от  командного  окна  к  графическому  окну  и 

обратно) осуществляется   с помощью комбинации клавиш<Alt+Tab>  или с 
помощью мыши.  

В общем случае, число аргументов у функции plot() не ограничивается 

двумя. Эта функция имеет следующий формат:   

plot(x1,y1,x2,y2,...).  
Таким образом, в одном графическом окне можно построить не один, а 

несколько  графиков.  Рассмотрим  два  способа  построения  в  одном 
графическом окне 3-х графиков (рис.1.2.2-3): 

Рис. 1.2.2-3. Использование векторов значений функций 

для построения графиков 3-х функций 

Рис. 1.2.2-4. Использование матрицы значений функций 

для построения графиков 3-х функций 

38 

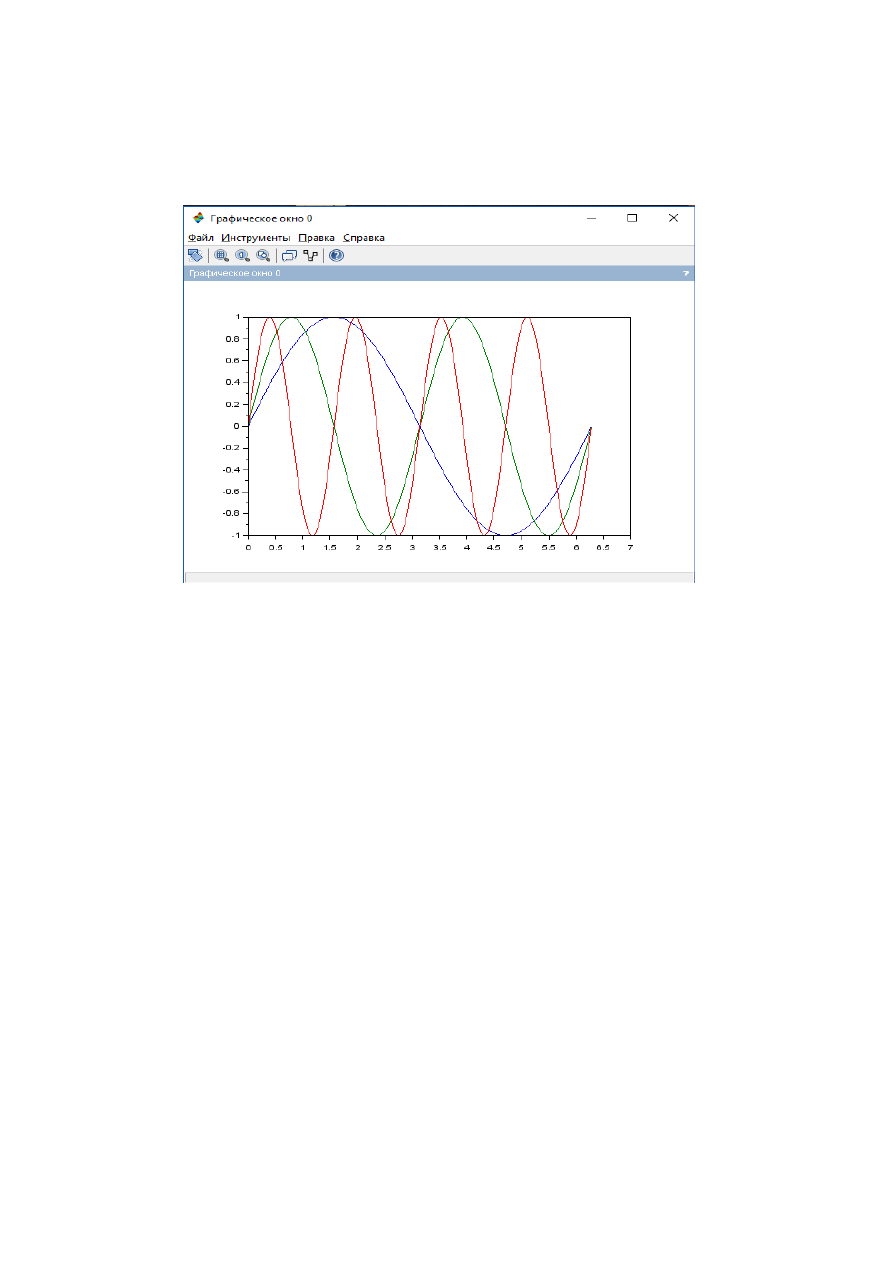
Приведенные в первом и втором примерах наборы команд позволяют 

получить один и тот же результат (рис. 1.2.2-5.) Разница в том, что в первом 
примере формируется три вектора значений функций (y1, y2, y3), а во втором 
– матрица y, содержащая значения функций в виде столбцов.  

 
Рис1.2.2-5. Графики функцийy1=sin(x); y2=sin(2*x);y3=sin(4*x) 
 
График,  выведенный  в  графическое  окно  Scilab,  может  быть  снабжен 

заголовком,  именами  осей,  дополнительным  текстом,  сеткой  и  другой 
поясняющей 

информацией. 

Аргументами 

команд, 

управляющими 

пояснениями,  являются  текстовые  строки.  Например,  команда  xtitle('title', 
'xstr',  'ystr')  добавит  к  графику  заголовок  и  подписи  осей.  Команда  xgrid() 
позволяет отобразить координатную сетку.  

В  случаях,  когда  в  одной  координатной  плоскости  изображаются 

графики  нескольких  функций,  как  в  нашем  примере,  возникает 
необходимость в выводе обозначений («легенде»). Имена созданных кривых 
можно вывести с помощью команды legend: 

 
legend(leg1, leg2, ..., legn, [pos]), 
 
где: leg1 — имя первого графика; 
       leg2 — имя второго графика; 
       legn — имя n-го графика; 
       pos—числовой  параметр,  определяющий  место  расположения 

обозначений в графическом окне (табл. 1.2.2-1). 

39 

 Таблица 1.2.2-1 

Значение аргумента 

Размещение легенды 

-1 

В правом верхнем углу над областью графика 

0 

Место выбирается автоматически, чтобы не перекрывать 
область кривых 

1 

В правом верхнем углу (и по умолчанию) 

2 

В левом верхнем углу области графика 

3 

В левом нижнем углу области графика 

4 

В правом нижнем углу области графика 

 
При  выводе  в  одно  графическое  окно  нескольких  графиков  удобнее 

каждый  график  выводить  с использованием  своей  команды  plot(),  однако  в 
этом случае происходит создание нового графического окна. Для того, чтобы 
этого  избежать  используется  команда  mtlb_hold('on').  Эта  команда 
позволяет расположить все в дальнейшем выводимые графики в одном окне.  

При  выводе  графика  можно  сменить  принятый  по  умолчанию  Scilab 

цвет и тип точек, с помощью которых рисуется данный график (табл.1.2.2-2).  
Символы,  указывающие  на  цвет  и  тип  точки,  заключаются  в  апострофы  и 
указываются в команде plot()  после имени функции.  

Таблица 1.2.2-2 

Символ  Цвет 

Символ  Маркер 

y 

Желтый 

точка 

m 

фиолетовый 

. 

: 

c 

голубой 

x 

x-метка 

r 

красный 

+ 

плюс 

g 

зеленый 

* 

звездочка 

b 

синий 

s 

квадрат 

w 

белый 

d 

алмаз 

k 

черный 

v 

Треугольник(вниз) 

€ 

треугольник (вверх) 

- 

сплошная 

< 

треугольник (влево) 

точечная 

> 

треугольник (вправо) 

-. 

Штрих - пунктирная 

p 

шестиугольник 

- 

пунктирная 

h 

восьмиугольник 

 
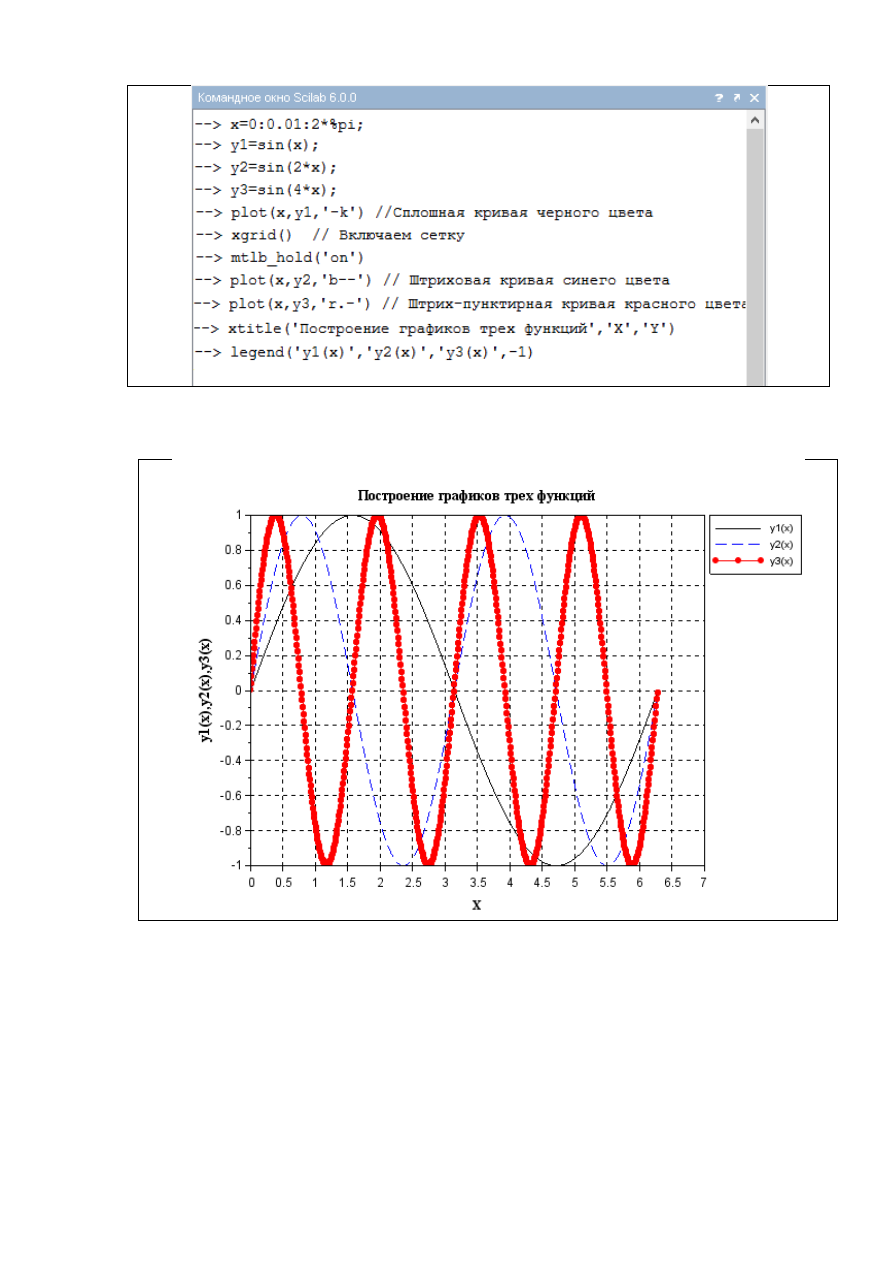
Рассмотрим  пример  (рис.  1.2.2-6),  в  котором  используются 

перечисленные  выше  опции,  инструкции  и  функции.  Результат  выполнения 
инструкций, комментирующих графики, приведен на рис.1.2. 2-7. 

40 

Рис. 1.2.2-6. Использование инструкций при построении графиков 

Рис. 1.2.2-7. Результат выполнения инструкций, 

комментирующих графики 

 
Большую  часть  вышеописанных  действий  можно  реализовать  также  с 

помощью  команд  инструментальной  панели  и  кнопок  графических  окон 
(рис.1.2.1-8).