Файл: Электронное пособие Scilab.pdf

31 

Scilab  обладает  большим  набором  встроенных  функций  для 

обработки  векторных  данных.    Полный  список  имеющихся  функций 
выводится в справке (

Справка Scilab>>Основные функции> Элементарные матрицы

). 

Некоторые из них приведены в таблице 1.2.1-1.  

Таблица 1.2.1-1 

Функции операции над векторами 

prod(V) 

Произведение элементов вектора 

sum(V) 

Сумма элементов вектора 

min(V) 

Минимальный элемент вектора 

max(V) 

Максимальный элемент вектора 

mean(V) 

Среднее значение элементов вектора 

gsort(V) 

Сортировка элементов вектора по убыванию 

Функции определения матриц и операций над ними 

det(A) 

Вычисляет определитель квадратной матрицы 

rand (n,m) 

Возвращает матрицу, элементы которой 
распределены по равномерному закону 

rand(n,m,”normal”)  Возвращает матрицу, элементы которой 

распределены по нормальному закону 

size(A) 

Определяет число строк и столбцов матрицыА, 
результат – вектор [n;m] 

sum(A [,k]) 

Формирует вектор-строку (k – есть) или вектор-
столбец (k- нет), каждый элемент которого – сумма 
элементов строки или столбца 

min(А) 

Формирует вектор-столбец из минимальных 
элементов строк 

max(А) 

Формирует вектор-столбец из максимальных 
элементов строк 

gsort(A) 

Упорядочивает элементы столбцов по убыванию 

norm(A [,p]) 

Возвращает норму матрицы (по умолчанию 
вычисляется 2-я норма) 

inv(A) 

Возвращает матрицу, обратную А 

32 

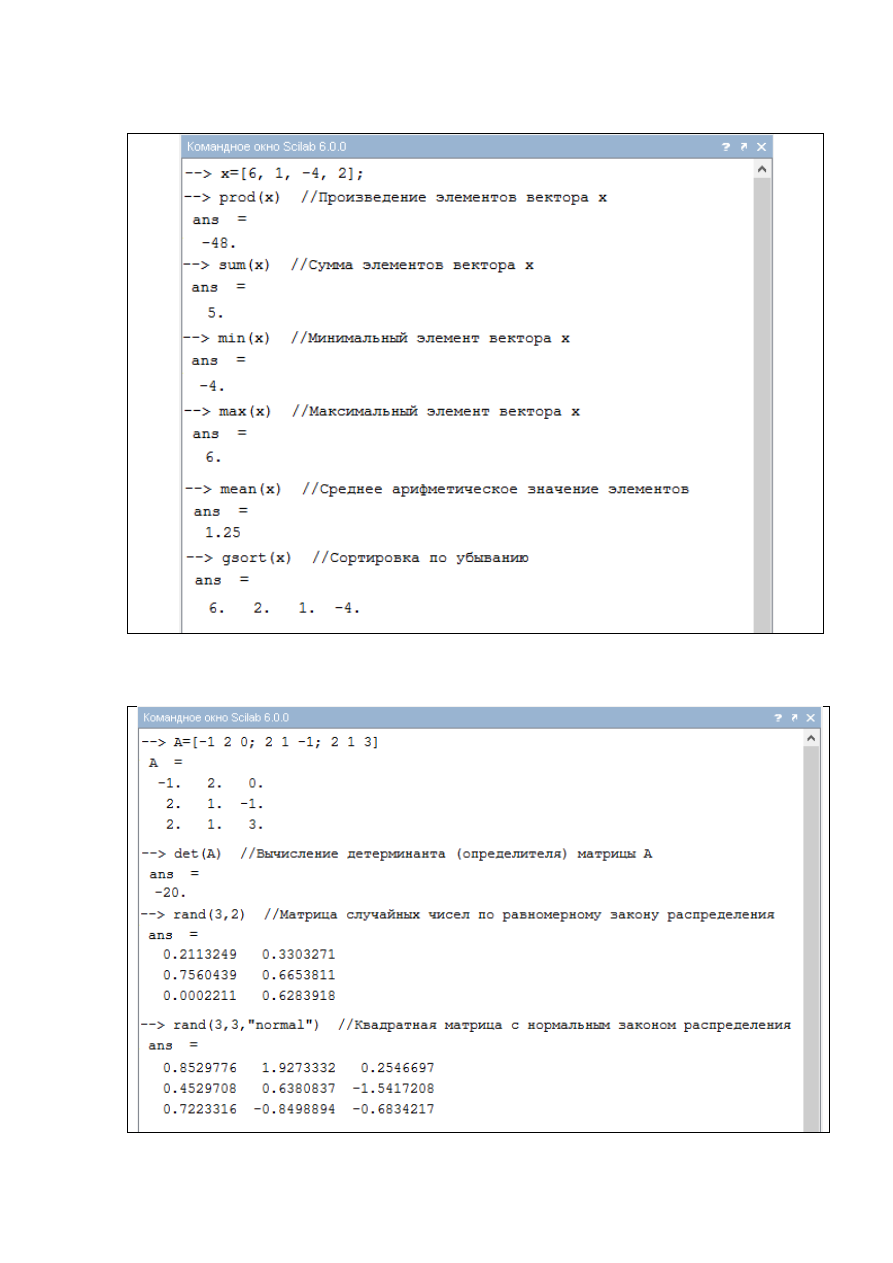
Примеры использования некоторых функций над векторами приведены 

на  рис. 1.2.1-6. 

Рис. 1.2.1-6. Примеры функции над векторами 

Рис. 1.2.1-7. Примеры определения матриц 

33 

На  рис.1.2.1-7  приведены  примеры  вычисления  определителя 

квадратной  матрицы  и  заполнения  матриц  случайными  числами, 
сгенерированных по равномерному и нормальному законам.  

В следующем примере (рис. 1.2.1-8) показано использование функции 

Scilab sum(). 

 
 Рис.1.2.1-8. Варианты использования функции Scilab sum() 
 
Пример,  приведенный  на  рис.1.2.1-9  демонстрирует  работу  функций, 

определяющих минимальное и максимальное значения матриц. 

Рис.1.2.1-9.  Определение минимальных и максимальных значений 

 
На  рис.1.2.1-10  показаны  применения  функций,  позволяющих 

определять  средние  значения  элементов  в  столбцах  (или  в  строках)  и 
проводить упорядочение (сортировку) элементов в строках (или столбцах).   

34 

Рис.1.2.1-10.  Определение средних значений и упорядочение элементов 

 
Известно,  что  если  детерминант  матрицы  отличен  от  нуля,  то  это 

невырожденная  матрица.  Для  такой  матрицы  может  быть  вычислена 
обратная  матрица  (А

-1

),  которая  при  умножении  на  исходную  матрицу  А, 

дает  единичную  (по  диагонали  расположены  единицы,  а  прочие  элементы 
равны нулю). Для получения обратной матрицы используется функция inv(). 
Умножение матриц в Scilab производится только с использованием их имен. 
Описанные действия приведены нарис.1.2.1-11. 

Рис. 1.2.1-11. Получение обратной и единичной матриц 

35 

Рассмотрим  еще  один  пример,  в  котором  матрица  умножается  на 

скаляр,  матрица  делится  на  скаляр,  и  матрица  умножается  на  вектор 
(рис.1.2.1-12).  

Рис. 1.2.1-12. Действия над матрицами 

Вектора и матрицы кроме традиционного их применения для хранения 

и обработки данных необходимы и для построения графиков функций. При 
этом  вектора  используются  для  построения  плоских  графиков  (графиков 
функций  от  одной  переменной),  а  матрицы  –  для  построения  трехмерных 
изображений (графиков функций от двух переменных).  

 
Обратите внимание, что после ввода или формирования элементов 

векторов  и  матриц  могут  возникнуть  ошибки.  Для  контроля  и 
исправления  отдельных  элементов  векторов  и  матриц  можно 
воспользоваться окном редактора данных (рис. 1.2.1-13). 
 

Окно  редактора  переменных  состоит  из  панели  инструментов  и 

области просмотра значений переменных. В окне редактора переменных (рис. 
1.2.1-13) можно отображать несколько переменных и редактировать значения 
используемых переменных. Переключение между переменными реализуется с 
помощью вкладок.