Файл: Компьютерное моделирование контрольная работа.doc

Таблица 14

Продолжение табл. 14

Вариант № 17.

При построении и испытаниях имитационной модели использовать данные столбцов «Y», «х₁», «х₂», «х₃» из табл. 15.

Вариант № 18.

При построении и испытаниях имитационной модели использовать данные столбцов «Y», «х₂», «х₃», «х₄» из табл. 15.

Таблица 15

Вариант № 19.

При построении и испытаниях имитационной модели использовать данные столбцов «Y», «х₁», «х₂», «х₃» из табл. 16.

Вариант № 20.

При построении и испытаниях имитационной модели использовать данные столбцов «Y», «х₂», «х₃», «х₄» из табл. 16.

Таблица 16

Вариант № 21.

При построении и испытаниях имитационной модели использовать данные столбцов «Y», «х₁», «х₂», «х₃» из табл. 17.

Вариант № 22.

При построении и испытаниях имитационной модели использовать данные столбцов «Y», «х₂», «х₃», «х₄» из табл. 17.

Таблица 17

Продолжение табл. 17

Вариант № 23.

При построении и испытаниях имитационной модели использовать данные столбцов «Y», «х₁», «х₂», «х₃» из табл. 18.

Вариант № 24.

При построении и испытаниях имитационной модели использовать данные столбцов «Y», «х₄», «х₅», «х₆» из табл. 18.

Таблица 18

Продолжение табл. 18

Вариант № 25.

При построении и испытаниях имитационной модели использовать данные столбцов «Y», «х₁», «х₂», «х₃» из табл. 19.

Таблица 19

Вариант № 26.

При построении и испытаниях имитационной модели использовать данные столбцов «Y», «х₄», «х₅», «х₆» из табл. 19.

Краткие теоретические сведения

Полученные в результате каких-либо исследований данные почти всегда представлены в виде таблиц. Числовые данные, содержащиеся в таблицах, обычно имеют между собой явные (известные) или неявные (скрытые) связи.

Явно связаны показатели, которые получены методами прямого счета, т. е. вычислены по заранее известным формулам. Например, проценты выполнения плана, уровни, удельные веса, отклонения в сумме, отклонения в процентах, темпы роста, темпы прироста, индексы и т. д.

Связи же второго типа заранее неизвестны. Однако люди должны уметь объяснять и предсказывать (прогнозировать) сложные явления, поведение объектов или систем для того, чтобы управлять ими. Поэтому специалисты с помощью наблюдений стремятся выявить скрытые зависимости и выразить их в виде формул, т. е. математически смоделировать явления или процессы. Одну из таких возможностей предоставляет корреляционно-регрессионный анализ.

Пользуясь методами корреляционно-регрессионного анализа, аналитики измеряют тесноту связей показателей с помощью коэффициента корреляции. При этом обнаруживаются связи, различные по силе (сильные, слабые, умеренные и др.) и различные по направлению (прямые, обратные). Если связи окажутся существенными, то целесообразно будет найти их математическое выражение в виде регрессионной модели и оценить статистическую значимость модели. В экономике значимое уравнение используется, как правило, для прогнозирования изучаемого явления или показателя.

Корреляционно-регрессионный анализ связей между переменными показывает, как один набор переменных (X) может влиять на другой набор (У). Таким образом, регрессионные вычисления и подбор хороших уравнений - это ценный, универсальный исследовательский инструмент в самых разнообразных отраслях деловой и научной деятельности (маркетинг, торговля, медицина, техника и т. д.).

Рассмотрим этапы корреляционно-регрессионного анализа данных.

Нулевой этап - это сбор данных. Как в строительстве нулевой цикл обеспечивает фундамент будущему зданию, так в корреляционно-регрессионном анализе решающую роль играет качество данных. Сбор данных создает фундамент прогнозам. Поэтому имеется ряд требований и правил, которые следует соблюдать при сборе данных.

Данные должны быть наблюдаемыми, т. е. полученными в результате замера, а не расчета. Наблюдения следует спланировать. Чем больше неодинаковых (не повторяющихся) данных, и чем они однороднее, тем лучше получится уравнение, если связи существенны. Подозрительные данные могут быть вызваны ошибками наблюдений и экспериментов.

Первый этап - корреляционный анализ. Его цель - определить характер связи (прямая, обратная) и силу связи (связь отсутствует, связь слабая, умеренная, заметная, сильная, весьма сильная, полная связь). Корреляционный анализ создает информацию о характере и степени выраженности связи (коэффициент корреляции), которая используется для отбора существенных факторов, а также для планирования эффективной последовательности расчета параметров регрессионных уравнений. При одном факторе вычисляют коэффициент корреляции, а при наличии нескольких факторов строят корреляционную матрицу, из которой выясняют два вида связей: связи зависимой переменной с независимыми, связи между самими независимыми.

Для определения тесноты связи результативного признака у с определяющими его х1, х2, х3 и влияния определяющих признаков друг на друга вычисляются парные коэффициенты корреляции r_yx1, r_yx2, r_yx3, r_x1x2, r_x1x3, r_x2x3.

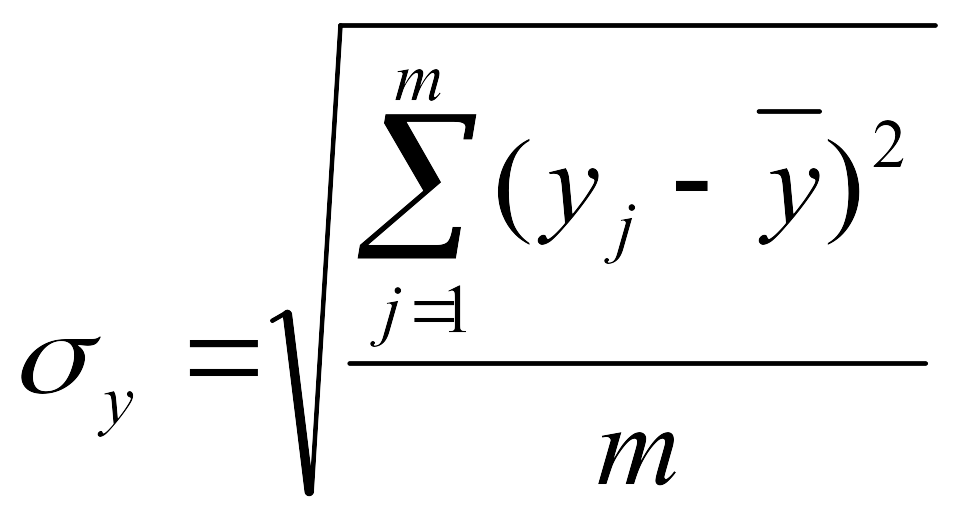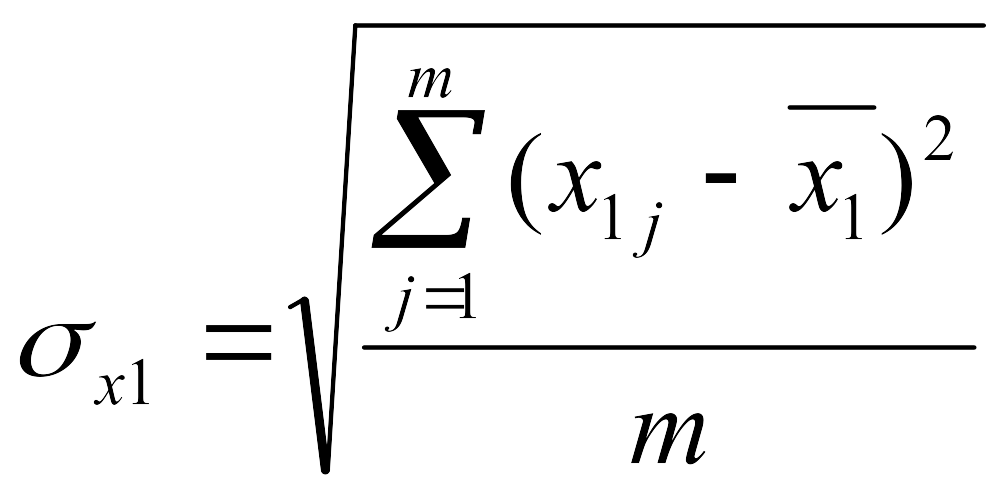, где - выборочное среднее значение переменных х₁, у по всем группам значений переменных, , , где m – количество групп исследуемых изделий, размерность выборки. Аналогично рассчитываются значения r_yx2, r_yx3 по приведённым выше формулам, только переменная х₁ заменяется на х₂ или на х₃ соответственно. Аналогично рассчитываются коэффициенты корреляции определяющих признаков друг на друга:

,

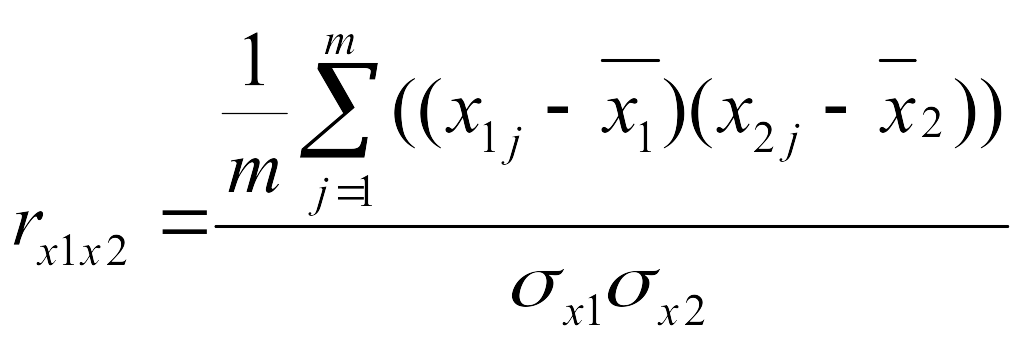
где - выборочное среднее значение переменных х₁, x₂ по всем группам значений переменных,

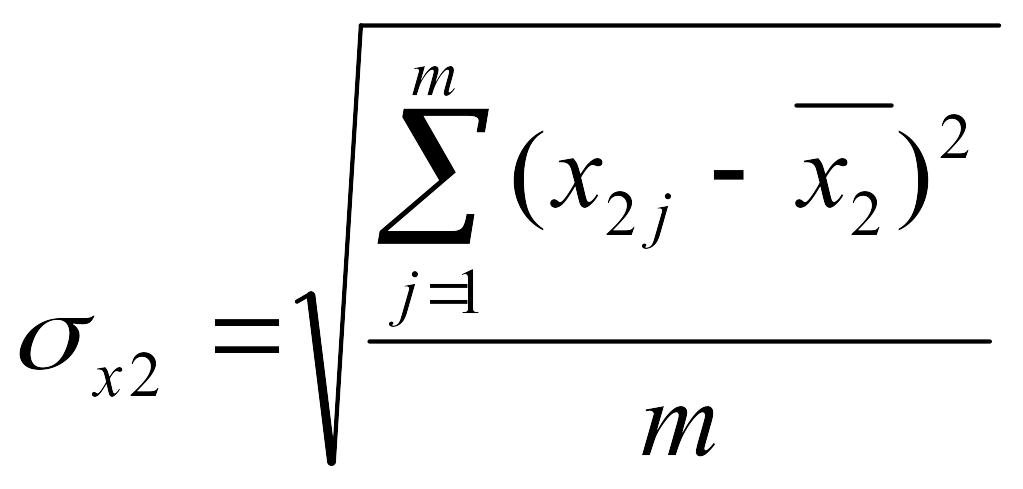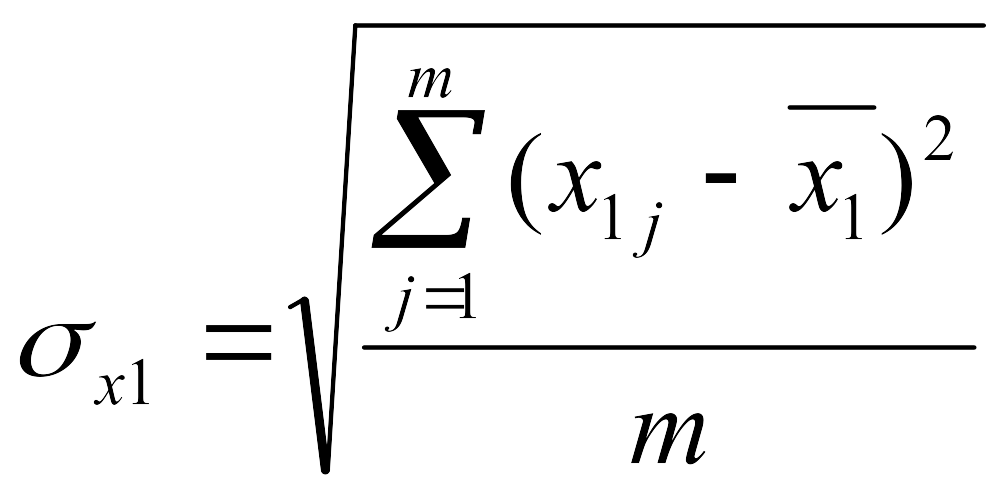, , где m – количество групп исследуемых изделий, размерность выборки.

В библиотеке функций табличного процессора MS Excel есть статистическая функция КОРРЕЛ() для вычисления парных коэффициентов корреляции.

Второй этап - расчет параметров и построение регрессионных моделей. Здесь стремятся отыскать наиболее точную меру выявленной связи, для того чтобы можно было прогнозировать, предсказывать значения зависимой величины Y, если будут известны значения независимых величин Х₁, Х₂, …, Х_n. Эту меру можно выразить математической моделью линейной множественной регрессионной зависимости: у = а₀ + b₁x₁ + b₂x₂ + … + b_n x_n.

Для нахождения коэффициентов используют метод наименьших квадратов. Смысл метода в том, что строят функционал:

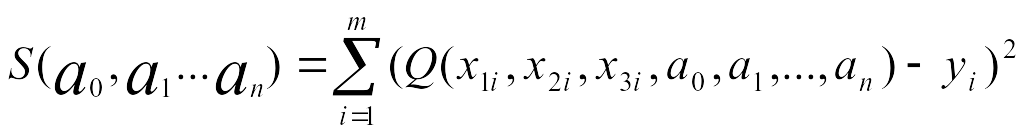, затем он минимизируется .

Для решения поставленной задачи составляется система уравнений:

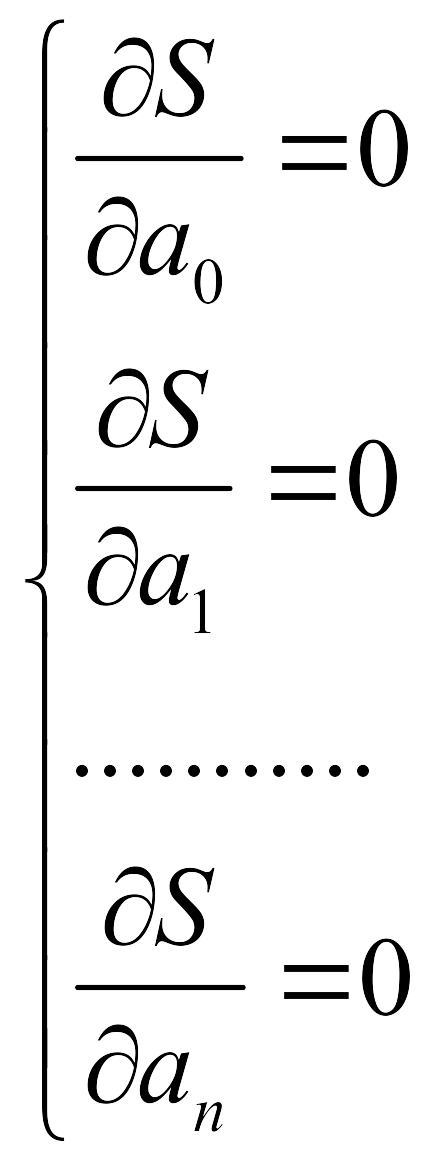, что эквивалентно

Для

система уравнений имеет вид:

После выполнения несложных эквивалентных преобразований получаем систему уравнений:

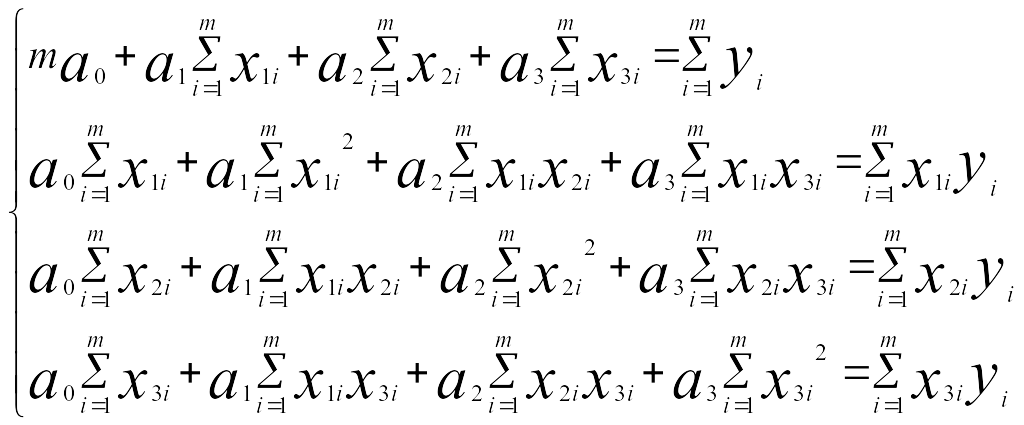
Решением данной системы являются коэффициенты уравнения регрессии а₀, а₁, а₂, а₃. Их значения можно получить, например, методом Крамера.

Осуществление второго этапа сильно зависит от выводов, которые получены при анализе корреляционной матрицы. Можно значительно ускорить проведение регрессионного анализа и снизить затраты на исследование, если принять правильную стратегию поиска наилучшего уравнения. Для этого необходимо знать основные и наиболее эффективные методы поиска наилучшего уравнения.

После получения каждого варианта уравнения обязательной процедурой является оценка его статистической значимости, поскольку главная цель - получить уравнение наивысшей значимости, поэтому второй этап корреляционно-регрессионного анализа неразрывно связан с третьим. Однако в связи с тем, что расчеты выполняет ЭВМ, а решение на основе оценки значимости уравнения принимает исследователь (принять или отбросить уравнение), условно можно выделить третий этап этой человеко-машинной технологии как интеллектуальный немашинный этап, для которого почти все данные по оценке значимости уравнения подготавливает ЭВМ.

На третьем этапе выясняют статистическую значимость, т. е. пригодность постулируемой модели для использования ее в целях предсказания значений отклика. Задачей третьего этапа построения регрессионных моделей является вычис­ление коэф­фи­циента детерминации или коэффициента множественной корреляции, на основании которого можно сделать заключение о значимости построенной регрессионной модели и возможности её дальнейшего исполь­зования для объяснения и анализа процессов, прояв­ляющихся, в данной задаче. Коэффициент множественной корреляции определяется по формуле: R_xy = , где K_x^{- 1} – обратная матрица корреляции, а матрица корреляции для трёх факторных признаков x₁, x₂ имеет вид: . Причём корреляционная матрица любой размерности будет симметричной, так как r_xiхj = r_xjхi. Для трёх факторных признаков вектор = - вектор коэффициентов парной регрессии результативного признака Y и факторных признаков X₁, X₂, X₃.

На этом этапе исключительно важную роль играют коэффициент детерминации и F-критерий значимости регрессии. R_xy² = D = R_xy Squared - коэффициент детерминации - это квадрат множественного коэффициента корреляции между наблюдаемым значением Y и его теоретическим значением, вычисленным на основе модели с определенным набором факторов. Коэффициент детерминации измеряет действительность модели. Он может принимать значения от 0 до 1. Эта величина особенно полезна для сравнения ряда различных моделей и выбора наилучшей модели.