ВУЗ: Смоленский областной казачий институт промышленных технологий и бизнеса
Категория: Задание
Дисциплина: Моделирование систем
Добавлен: 19.11.2018
Просмотров: 3253
Скачиваний: 7
СОДЕРЖАНИЕ
2. Порядок выбора варианта задания контрольной работы, сдачи и защиты контрольных работ
3. Требования к оформлению и содержанию контрольных работ
4. Задания контрольной работы и методические рекомендации для их выполнения
Краткие теоретические сведения для выполнения задания контрольной работы № 1
ПРИМЕР выполнения и оформления задания № 1 контрольной работы
Краткие теоретические сведения по теме задания
Краткие теоретические сведения
Краткие теоретические сведения
Краткие теоретические сведения
Вариант 14.
Рассчитать вероятности состояний, среднее число заявок в системе, среднюю длину очереди, вероятность обслуживания заявок в СМО с ожиданиями, если количество каналов n=3, длина очереди l=2.
Вариант 15.
Рассчитать вероятности состояний, среднее число заявок в системе, среднюю длину очереди, вероятность обслуживания заявок в СМО с ожиданиями, если количество каналов n=3, длина очереди l=3.
Вариант 16.
Рассчитать вероятности состояний, среднее число заявок в системе, среднюю длину очереди, вероятность обслуживания заявок в СМО с ожиданиями, если количество каналов n=3, длина очереди l=4.
Вариант 17.
Рассчитать вероятности состояний, среднее число заявок в системе, среднюю длину очереди, вероятность обслуживания заявок в СМО с ожиданиями, если количество каналов n=3, длина очереди l=4.
Вариант 18.
Рассчитать вероятности состояний, среднее число заявок в системе, среднюю длину очереди, вероятность обслуживания заявок в СМО с ожиданиями, если количество каналов n=3, длина очереди l=5.
Вариант 19.
Рассчитать вероятности состояний, среднее число заявок в системе, среднюю длину очереди, вероятность обслуживания заявок в СМО с ожиданиями, если количество каналов n=3, длина очереди l=6.
Вариант 20.
Рассчитать вероятности состояний, среднее число заявок в системе, среднюю длину очереди, вероятность обслуживания заявок в СМО с ожиданиями, если количество каналов n=4, длина очереди l=1.
Вариант 21.
Рассчитать вероятности состояний, среднее число заявок в системе, среднюю длину очереди, вероятность обслуживания заявок в СМО с ожиданиями, если количество каналов n=4, длина очереди l=2.
Вариант 22.
Рассчитать вероятности состояний, среднее число заявок в системе, среднюю длину очереди, вероятность обслуживания заявок в СМО с ожиданиями, если количество каналов n=4, длина очереди l=3.
Вариант 23.
Рассчитать вероятности состояний, среднее число заявок в системе, среднюю длину очереди, вероятность обслуживания заявок в СМО с ожиданиями, если количество каналов n=4, длина очереди l=4.
Вариант 24.
Рассчитать вероятности состояний, среднее число заявок в системе, среднюю длину очереди, вероятность обслуживания заявок в СМО с ожиданиями, если количество каналов n=4, длина очереди l=5.
Вариант 25.
Рассчитать вероятности состояний, среднее число заявок в системе, среднюю длину очереди, вероятность обслуживания заявок в СМО с ожиданиями, если количество каналов n=5, длина очереди l=1.
Вариант 26.
Рассчитать вероятности состояний, среднее число заявок в системе, среднюю длину очереди, вероятность обслуживания заявок в СМО с ожиданиями, если количество каналов n=5, длина очереди l=2.
Вариант 27.
Рассчитать вероятности состояний, среднее число заявок в системе, среднюю длину очереди, вероятность обслуживания заявок в СМО с ожиданиями, если количество каналов n=5, длина очереди l=3.
Вариант 28.
Рассчитать вероятности состояний, среднее число заявок в системе, среднюю длину очереди, вероятность обслуживания заявок в СМО с ожиданиями, если количество каналов n=5, длина очереди l=4.
Вариант 29.
Рассчитать вероятности состояний, среднее число заявок в системе, среднюю длину очереди, вероятность обслуживания заявок в СМО с ожиданиями, если количество каналов n=6, длина очереди l=2.
Вариант 9.
Рассчитать вероятности состояний, среднее число заявок в системе, среднюю длину очереди, вероятность обслуживания заявок в СМО с ожиданиями, если количество каналов n=6, длина очереди l=3.
Изучив размещённые ниже теоретические сведения, студент должен выполнить задание выбранного варианта. Решение задания на расчёт параметров СМО начинается с описания состояний системы массового обслуживания и построения её графа. Далее студентом составляется система уравнений Колмогорова, по которой строится имитационная модель.
Методика расчёта показателей СМО и вероятностей её состояний для разных видов СМО приводится ниже в настоящем пособии. Для любой СМО обязательно необходимо составить систему уравнений Колмогорова и рассчитать вероятности состояний системы.
Рекомендуется разрабатывать имитационную модель на VBA for Excel. Это условие не является обязательным. Студент может разрабатывать имитационную модель, используя любое инструментальное средство, например, Borland DELPHI 6 (7), Borland JBuilder 7, Visual Basic, CBuilder и т.д.
По результатам выполнения данного задания контрольной работы должны быть представлены следующие материалы:
- указание типа СМО, её описание;
- изображение графа СМО, описание её состояний;
- запись системы уравнений Колмогорова;
- внешний вид интерфейса разработанной имитационной модели;
- структуру программного обеспечения имитационной модели с указанием средства разработки;
- описание функций модулей (классов) и других элементов программного обеспечения имитационной модели;
- порядок использования имитационной модели.
ПРИМЕР выполнения и оформления задания № 1 контрольной работы
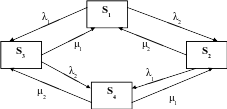 СМО
представляет собой техническое
устройство, состоящее из двух узлов,
которые могут независимо друг от друга
выходить из строя. Граф системы массового
обслуживания представлен на рис. 10.
СМО
представляет собой техническое
устройство, состоящее из двух узлов,
которые могут независимо друг от друга
выходить из строя. Граф системы массового
обслуживания представлен на рис. 10.
Рис. 10.
СМО может находиться в следующих состояниях:
S1 – оба узла исправны, техническое устройство выполняет свои функции;
S2 – первый узел исправен и работает, второй – неисправен;
S3 – первый узел неисправен, второй узел исправен;
S4 – оба узла неисправны, техническое устройство ремонтируется.
λ1 – поток неисправностей первого узла; μ1 – поток ремонтов первого узла;
λ2 – поток неисправностей второго узла; μ2 – поток ремонтов второго узла.
Каждому из состояний можно поставить в соответствие вероятность нахождения СМО в данном состоянии:
- S1 соответствует вероятность p1;
- S2 соответствует вероятность p2;
- S3 соответствует вероятность p3;
- S4 соответствует вероятность p4.
По графу системы массового обслуживания составляем систему уравнений Колмогорова (1), по которой можно определить вероятности состояний системы. Для этого следует исключить одно из уравнений системы, затем решить полученную неоднородную систему линейных уравнений любым методом (Крамера, Гаусса).
![]() (1)
(1)
Рассмотрим пример имитационной модели, позволяющей исследовать описанную выше СМО. Имитационная модель разработана средствами VBA for Excel и табличного процессора MS Excel. Интерфейс имитационной модели представлен на рис. 11.

Рис. 11. Интерфейс имитационной модели
Основными элементами управления имитационной модели исследования параметров СМО являются кнопки, с которыми связаны соответствующие макросы. Основные функции и операции, реализованные в имитационной модели СМО:
- ввод показателей СМО (количества каналов обслуживания, интенсивности потоков неисправностей узлов технического устройства, интенсивности потоков ремонтов узлов технического устройства);
- формирование системы уравнений Колмогорова (см. систему уравнений 1);
- расчёт главного определителя системы уравнений Колмогорова;
- расчёт первого определителя системы уравнений Колмогорова;
- расчёт второго определителя системы уравнений Колмогорова;
- расчёт третьего определителя системы уравнений Колмогорова;
- расчёт четвёртого определителя системы уравнен
Для ввода параметров СМО используется объект UserForm1, который вызывается по нажатию одноимённой кнопки (см. рис. 12).
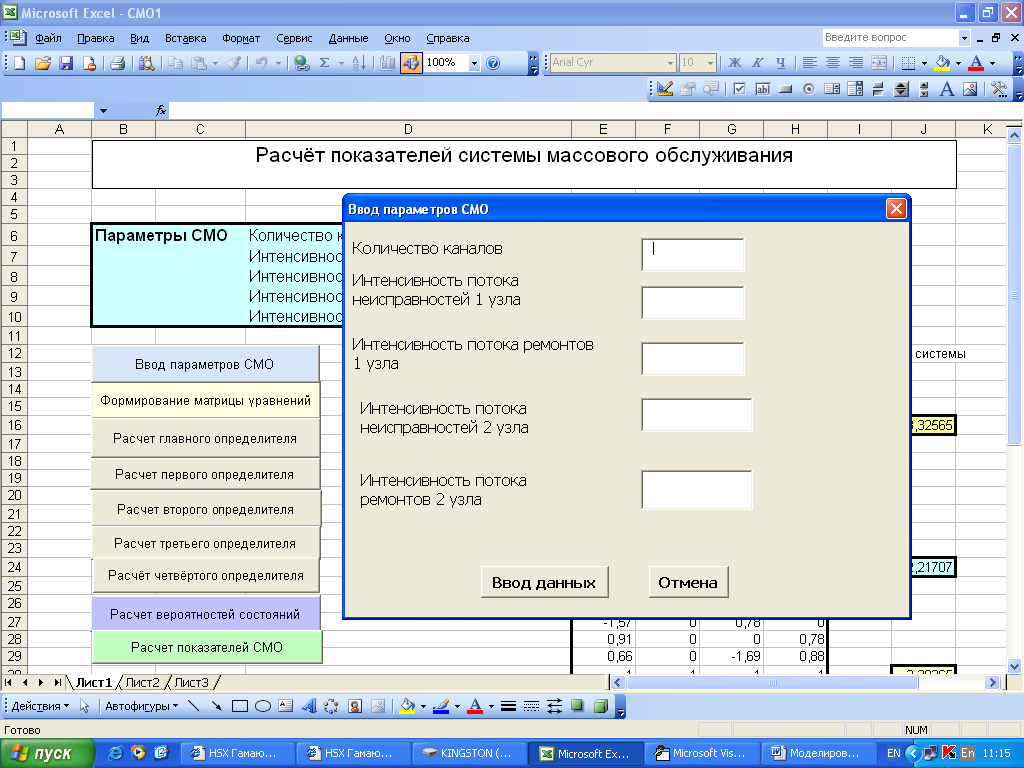
Рис. 12. Форма ввода параметров СМО
Для выполнения все указанных выше функций имитационной модели записываются макросы в автоматическом режиме. Для этого выбирают пункт меню «Сервис», закладку «Макрос» - «Начать запись». Именуют макрос, затем выполняют требуемую для расчётов последовательность действий, после чего нажимают кнопку или закладку «Макрос» - «Остановить запись». Для расчёта определителей используется математическая функция МОПРЕД(), которая в режиме макроса вычисляет нужный определитель.
Статические эксперименты в построенной моделью двухканальной СМО с отказами можно выполнять, варьируя параметры СМО (интенсивности потоков неисправностей узлов технического устройства и потоков их ремонтов). Можно пронаблюдать как изменение параметров СМО влияет на результаты её функционирования – на вероятности состояний, относительную пропускную способность.
Краткие теоретические сведения по теме задания
В повседневной жизни к системам массового обслуживания относятся телефонные и автозаправочные станции, билетные кассы, торговые предприятия, парикмахерские, мастерские и т.п. В таких системах два основных потока: входной — поток заявок и выходной поток обслуживания. Поток заявок образуют клиенты (покупатели), желающие приобрести какой-либо товар. Выходной поток образуют продавцы, обслуживающие покупателей. Если интенсивность обслуживания мала, то образуется очередь. Последнюю можно ликвидировать или быстро сократить, используя несколько каналов обслуживания (несколько телефонных аппаратов, билетных касс, торговых точек и т.д.).
Для того, чтобы понять, как решаются такие задачи массового обслуживания, рассмотрим сначала основные понятия и определения.
Теория систем массового обслуживания (СМО) впервые была разработана датским математиком А. К. Эрлангом применительно к запросам, поступающим на телефонную станцию. Поэтому основные понятия и определения сохраняются из практики обеспечения телефонной связи независимо от фактического назначения конкретной СМО.
Системы массового обслуживания предназначены для обслуживания потока заявок или требований, поступающих на вход в случайные моменты времени. Каждая СМО состоит из некоторого числа каналов обслуживания, в качестве которых в зависимости от вида системы могут выступать: линии связи, приемные пункты, рабочие точки, подъездные пути, испытательные стенды, технологические агрегаты, ремонтные бригады и т.д. Выполнение поступившей заявки, т.е ее обслуживание, продолжается некоторое время (тоже случайное), после чего канал освобождается и готов принять следующую заявку.
Поступающие на вход системы массового обслуживания требования-заявки следуют одно за другим и образуют непрерывный поток событий. Конечно, невозможно заранее предсказать, например, когда какому-то абоненту вздумается позвонить по телефону своему партнеру, но если рассматривать всех абонентов телефонной станции, то несмотря на случайный характер каждого отдельного события, за 1 час (60 мин) было, например, 30 телефонных вызовов, то в среднем одна заявка приходится на интервал в 2 мин. Следовательно, среднее число событий в единицу времени — интенсивность потока λ — будет равна 0.5.
В простейшем потоке интенсивность является постоянной величиной, т.е λ=const во времени. Такие простейшие потоки называются стационарными.
Системы массового обслуживания могут быть двух типов: СМО с отказами, в которых заявка, поступившая в тот момент, когда все каналы заняты, получает отказ и не обслуживается; СМО с ожиданием, в которых каждая заявка, прибывшая в систему, когда в ней нет свободных каналов, остается и ожидает, пока освободится какой-нибудь канал и ее возьмут на обслуживание. По аналогии с системами обслуживания населения ожидающие заявки называют очередью.
Основы теории СМО рассмотрим на примере. Пусть производственная система состоит из двух устройств, каждое из которых производит одну и ту же продукцию. Устройства в ходе работы могут выйти из строя (отказать). Отказавшее устройство немедленно начинают ремонтировать.
Г раф
состояний такой производственной
системы будет следующим (рис. 13):
раф
состояний такой производственной
системы будет следующим (рис. 13):
μ2
Рис. 13. Граф состояний производственной системы
Рассматриваемая система имеет четыре состояния:
S1 — оба устройства работают;
S2 — первое устройство ремонтируется (после отказа), второе работает;
S3 — второе ремонтируется, первое работает; S4 — оба ремонтируются.
Переходы S1 - S2; S2 – S4; S1 - S3; S3 – S4 совершаются в результате происходящих в системе отказов. Обратные переходы являются следствием ремонтных работ. Отказы и окончания — являются случайными величинами.
Пусть λ1 — интенсивность потока отказов первого устройства; λ2— интенсивность потока отказов второго устройства; μ1 — интенсивность потока окончаний ремонтов первого устройства; μ2 — интенсивность потока окончаний ремонтов второго устройства.
Рассмотрим
конкретное состояние, например S1.
Из этого состояния возможны переходы
в состояния S2
и S3
— с суммарной вероятностью λ1
+
λ2,
отнесенной к единице времени. В
стационарном режиме интенсивность
потока событий равна вероятности за
конечный промежуток времени, деленной
на этот промежуток времени. Таким
образом, число уходов из состояния S1,
в единицу времени в рассматриваемом
коллективе систем равно:
![]()
Здесь видно общее правило: совершаемое в единицу времени число переходов Si в Sj равно произведению числа систем в состоянии Si (в исходном состоянии) на вероятность перехода, отнесенную к единице времени. Мы рассмотрели уходы из состояния S1.
Приходы
в это состояние совершаются из S2
и S3.
Поскольку рассматривается стационарный
режим, то числа уходов и приходов для
каждого состояния должны быть
сбалансированы. Следовательно:
![]()
Это уравнения Колмогорова, записанные для системы, граф состояний которой показан на рис. 13. Рассуждая аналогичным образом, можно составить уравнения Колмогорова и для других СМО.
Рассматривая баланс уходов и приходов для каждого из четырех состояний и сокращая в уравнениях общий множитель N, получаем следующие уравнения относительно вероятностей р1, р2, р3, р4:
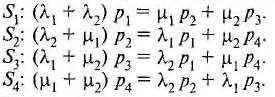
Нетрудно убедиться, что четвертое уравнение может быть получено сложением первых трех. Вместо этого уравнения воспользуемся уравнением: p1 + р2 + р3 + р4 = 1, которое означает, что система с достоверностью находится в каком-либо из четырех состояний. Таким образом, приходим к системе уравнений:


Примеры задач с СМО
Задача № 1. Имеется производственная система, производящая некоторую продукцию. Граф состояний такой системы показан на рис. 13. Предположим, что второе устройство в данной системе более современное и имеет производительность вдвое более высокую, чем первое устройство. Первое устройство приносит в единицу времени доход, равный 5 условным единицам, а второе — 10 единицам. Отказы второго устройства происходят в среднем вдвое чаше, чем первого; поэтому положим, что λ1= 1, λ2= 2. Интенсивности потоков окончаний ремонтов примем равными μ1= 2, μ2 = 3. Используя заданные интенсивности отказов и потоков окончаний ремонтов, перепишем уравнения Колмогорова в виде:
Решая эту систему уравнений, находим: р1= 0.4; р2 = 0.2; р3 = 0.27; р4 = 0.13, Это означает, что в среднем 40% времени оба устройства работают одновременно (состояние S1 на рис. 13); 20% времени работает только первое устройство, а второе при этом ремонтируется (состояние S2); 21% времени работает только второе устройство, а первое при этом ремонтируется (состояние S3); 13% времени оба устройства одновременно находятся в состоянии ремонта (состояние S4). Нетрудно подсчитать доход, которой дает система из двух рассматриваемых устройств в единицу времени: (5 + 10) х 0.4 + 5 * 0.2 + 10х 0.27 = 9.7 усл. ед.