ВУЗ: Смоленский областной казачий институт промышленных технологий и бизнеса
Категория: Задание
Дисциплина: Моделирование систем
Добавлен: 19.11.2018
Просмотров: 3266
Скачиваний: 7
СОДЕРЖАНИЕ
2. Порядок выбора варианта задания контрольной работы, сдачи и защиты контрольных работ
3. Требования к оформлению и содержанию контрольных работ
4. Задания контрольной работы и методические рекомендации для их выполнения
Краткие теоретические сведения для выполнения задания контрольной работы № 1
ПРИМЕР выполнения и оформления задания № 1 контрольной работы
Краткие теоретические сведения по теме задания
Краткие теоретические сведения
Краткие теоретические сведения
Краткие теоретические сведения
Вариант 19. Разработать структурную схему цифрового устройства, которое на последовательно подаваемые входные сигналы Х1=1 выдаёт последовательность двоичных чисел, совпадающих с двоичным кодом состояний элементарных цифровых автоматов 1, 3, 0, 2, 1, 3 и т. д., а на последовательно подаваемые входные сигналы Х2=1 выдаёт последовательность 3, 2, 1, 0, 3, 2 и т. д. Сигналы Х1=Х2=0 не изменяют состояние автомата. Одновременная подача сигналов Х1=1 и Х2 =1 исключается. В качестве модели принять автомат Мура. В качестве элементарных автоматов использовать T-триггеры. Для построения схемы выбрать логические элементы «И», «ИЛИ», «НЕ», описание которых приводится ниже.
Вариант 20. Разработать структурную схему цифрового устройства, которое на последовательно подаваемые входные сигналы Х1=1 выдаёт последовательность двоичных чисел, совпадающих с двоичным кодом состояний элементарных цифровых автоматов 1, 3, 0, 2, 1, 3 и т. д., а на последовательно подаваемые входные сигналы Х2=1 выдаёт последовательность 3, 2, 1, 0, 3, 2 и т. д. Сигналы Х1=Х2=0 не изменяют состояние автомата. Одновременная подача сигналов Х1=1 и Х2 =1 исключается. В качестве модели принять автомат Мура. В качестве элементарных автоматов использовать Т-триггеры. Для построения схемы выбрать логические элементы «И», «ИЛИ», «НЕ», описание которых приводится ниже.
Вариант 21. Разработать структурную схему цифрового устройства, которое на последовательно подаваемые входные сигналы Х1=1 выдаёт последовательность двоичных чисел, совпадающих с двоичным кодом состояний элементарных цифровых автоматов 1, 3, 0, 2, 1, 3 и т. д., а на последовательно подаваемые входные сигналы Х2=1 выдаёт последовательность 3, 2, 1, 0, 3, 2 и т. д. Сигналы Х1=Х2=0 не изменяют состояние автомата. Одновременная подача сигналов Х1=1 и Х2 =1 исключается. В качестве модели принять автомат Мура. В качестве элементарных автоматов использовать Т- триггер. Для построения схемы выбрать логические элементы «И», «ИЛИ», «НЕ», описание которых приводится ниже.
Вариант 22. Разработать структурную схему цифрового устройства, которое на последовательно подаваемые входные сигналы Х1=1 выдаёт последовательность двоичных чисел, совпадающих с двоичным кодом состояний элементарных цифровых автоматов 1, 3, 0, 2, 1, 3 и т. д., а на последовательно подаваемые входные сигналы Х2=1 выдаёт последовательность 3, 2, 1, 0, 3, 2 и т. д. Сигналы Х1=Х2=0 не изменяют состояние автомата. Одновременная подача сигналов Х1=1 и Х2 =1 исключается. В качестве модели принять автомат Мура. В качестве элементарных автоматов использовать D- триггер. Для построения схемы выбрать логические элементы «И», «ИЛИ», «НЕ», описание которых приводится ниже.
Вариант 23. Разработать структурную схему цифрового устройства, которое на последовательно подаваемые входные сигналы Х1=1 выдаёт последовательность двоичных чисел, совпадающих с двоичным кодом состояний элементарных цифровых автоматов 1, 3, 0, 2, 1, 3 и т. д., а на последовательно подаваемые входные сигналы Х2=1 выдаёт последовательность 3, 2, 1, 0, 3, 2 и т. д. Сигналы Х1=Х2=0 не изменяют состояние автомата. Одновременная подача сигналов Х1=1 и Х2 =1 исключается. В качестве модели принять автомат Мура. В качестве элементарных автоматов использовать Т- триггер. Для построения схемы выбрать логические элементы «И», «ИЛИ», «НЕ», описание которых приводится ниже.
Вариант 24. Разработать структурную схему цифрового устройства, которое на последовательно подаваемые входные сигналы Х1=1 выдаёт последовательность двоичных чисел, совпадающих с двоичным кодом состояний элементарных цифровых автоматов 1, 3, 0, 2, 1, 3 и т. д., а на последовательно подаваемые входные сигналы Х2=1 выдаёт последовательность 0, 2, 1, 3, 0, 2 и т. д. Сигналы Х1=Х2=0 не изменяют состояние автомата. Одновременная подача сигналов Х1=1 и Х2 =1 исключается. В качестве модели принять автомат Мура. В качестве элементарных автоматов использовать D-триггеры. Для построения схемы выбрать логические элементы «И», «ИЛИ», «НЕ», описание которых приводится ниже.
Вариант 25. Разработать структурную схему цифрового устройства, которое на последовательно подаваемые входные сигналы Х1=1 выдаёт последовательность двоичных чисел, совпадающих с двоичным кодом состояний элементарных цифровых автоматов 1, 3, 0, 2, 1, 3 и т. д., а на последовательно подаваемые входные сигналы Х2=1 выдаёт последовательность 0, 2, 1, 3, 0, 2 и т. д. Сигналы Х1=Х2=0 не изменяют состояние автомата. Одновременная подача сигналов Х1=1 и Х2 =1 исключается. В качестве модели принять автомат Мура. В качестве элементарных автоматов использовать T-триггеры. Для построения схемы выбрать логические элементы «И», «ИЛИ», «НЕ», описание которых приводится ниже.
Краткие теоретические сведения для выполнения задания контрольной работы № 1
В терминах абстрактной алгебры алгебру логики можно определить как следующий объект: B = < M; S >, где М – множество-носитель, S – сигнатура алгебры. Объектами алгебры логики (алгебры Буля или алгебры высказываний – всё это эквивалентные понятия) являются высказывания – повествовательные предложения, которые в зависимости от конкретных условий могут принимать истинные или ложные значения. Истинные значения высказываний обозначаются логической «1», ложные значения высказываний обозначаются логическим «0». Поэтому множество- носитель алгебры логики можно записать следующим образом: М = {0(ложь), 1(истина)}. S – сигнатура алгебры представляет собой операции, которые можно выполнять над высказываниями, эти операции называются логическими и определяются следующими таблицами истинности.
1. Операция «Дизъюнкция», она ещё называется логическим сложением и обозначается « », задаётся таблицей истинности:
|
А |
В |
Y=АВ |
|
|
0 |
0 |
0 |
|
|
0 |
1 |
1 |
|
|
1 |
0 |
1 |
|
|
1 |
1 |
1 |
Рис. 1. Логический элемент «ИЛИ» |
2. Операция «Конъюнкция», она ещё называется логическим умножением и обозначается « », задаётся таблицей истинности:
|
А |
В |
Y=АВ |
|
|
0 |
0 |
0 |
|
|
0 |
1 |
0 |
|
|
1 |
0 |
0 |
|
|
1 |
1 |
1 |
|
3. Операция «Отрицание», она ещё называется логическим отрицанием или логическим «НЕ», операция отрицания переменной обозначается вертикальной чертой над этой переменной, задаётся таблицей истинности:
|
А |
Y
=
|
|
|
0 |
1 |
|
|
1 |
0 |
Рис. 3. Логический элемент «НЕ» |
Для построения комбинационных схем (схем без памяти), а также схем с памятью используются определённые выше логические элементы. Для синтеза автоматов с памятью кроме логических элементов ещё необходимо использовать элементы памяти.
В качестве элементов памяти в ЭВМ нашли широкое применение триггеры – электронные схемы с двумя устойчивыми состояниями. Эти элементы являются автоматами Мура и удовлетворяют следующим требованиям: 1) имеют два внутренних состояния, одно из которых кодируется цифрой 1, другое – 0; 2) каждому внутреннему состоянию соответствует свой выходной сигнал, позволяющий отличить одно состояние элементарного автомата от другого. Для удобства будем обозначать выходные сигналы элементарного автомата теми же буквами, что и состояние автомата. Для определения функций переходов элементарных автоматов введем следующие обозначения: q(t) – выходной сигнал, Q(t), Q(t+1) – состояние автомата в момент времени t и t+1 соответственно.
А
Рис. 4. Изображение
RS
- триггера
синхронный
RS
– триггер представляет собой триггер
с одним (или несколькими равноценными)
входом сброса триггера в нуль R
(Reset
- сброс) и одним (или несколькими
равноценными) входом установки триггера
в единицу S
(Set
– установка), меняющий свое состояние
асинхронно, вслед за изменением состояний
входных сигналов. Среди множества
возможных структур RS
– триггеров выделяют структуры триггеров
на элементах ИЛИ-НЕ и на элементах И-НЕ.
Таблица 1
Состояния и переходы RS – триггеров
|
qS(t) |
qR(t) |
Q(t) |
Q(t+1) |
Примечание |
|
|
0 |
0 |
0 |
0 |
|
Хранение |
|
0 |
0 |
1 |
1 |
||
|
0 |
1 |
0 |
0 |
|
Сброс в «0» |
|
0 |
1 |
1 |
0 |
||
|
1 |
0 |
0 |
1 |
|
Установка в «1» |
|
1 |
0 |
1 |
1 |
||
|
1 |
1 |
0 |
---- |
|
Запрещено |
|
1 |
1 |
1 |
---- |
||
На базе двухступенчатого RS – триггера путем замыкания обратных связей строится асинхронный T – триггер (Toggle – кувыркаться), т. е. триггер со счетным входом. С приходом каждого импульса на счетный вход триггер меняет свое состояние на противоположное.
Таблица 2
Таблица состояний и переходов Т - триггера
|
qT(t) |
Q(t) |
Q(t+1) |
|
0 |
0 |
0 |
|
0 |
1 |
1 |
|
1 |
0 |
1 |
|
1 |
1 |
0 |
Наибольшее применение нашел JK – триггер. J – вход установки триггера в единичное состояние (Jark – внезапное включение ), K – вход установки триггера в нулевое состояние (Kill – внезапное отключение). Функционирование триггера описывается таблицей.
Таблица 3
Таблица состояний и переходов JK - триггера
|
qJ(t) |
qK(t) |
Q(t+1) |
Примечание |
|
0 |
0 |
Q(t) |
Хранение |
|
0 |
1 |
0 |
Запись «0» |
|
1 |
0 |
1 |
Запись «1» |
|
1 |
1 |
|
Режим Т - триггера |
(
При создании узлов ЭВМ широкое применение находят D – триггеры, которые принимают информацию с входа D (Delay – задержка) по разрешающему сигналу синхронизации. D – триггер реализует задержку входного сигнала на один такт, т. е. Q(t+1)=qD(t).
Таблица 4
Таблица состояний и переходов D - триггера
|
Q(t)- Q(t+1) |
qD(t) |
|
0 - 0 |
0 |
|
0 - 1 |
1 |
|
1 - 0 |
0 |
|
1 - 1 |
1 |
Рис. 7. Изображение D- триггера
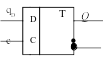
ПРИМЕР выполнения и оформления задания № 1 контрольной работы
Разработать структурную схему цифрового устройства, который на последовательно подаваемые входные сигналы х1=1 выдает последовательность двоичных чисел, совпадающих с двоичным кодом состояний элементарных цифровых автоматов 0, 2, 3, 1, 0, 2 и т. д. а на последовательно подаваемые входные сигналы х2=1 выдает последовательность 0, 3, 1, 2, 0, 3 и т. д.
Сигналы х1=х2=0 не изменяют состояние автомата. Одновременно подача сигналов х1=1 и х2=1 исключается. Так как выходные сигналы автомата зависят только от его состояния, то в качестве модели цифрового устройство принимаем автомат Мура. Число состояний автомата равно четырем, поэтому для его построения достаточно двух элементарных автоматов с полной системой переходов с выходов. В качестве элементарных автоматов принимаем Т – триггеры. Обозначим состояние и выходной сигнал первого триггера через Q1, а второго – через Q2. Т – триггеры имеют один функциональный вход, поэтому обозначим q1=qT1 q2=qT2
РЕШЕНИЕ
Исходя из условий работы автомата, построим его кодированную таблицу переходов (колонки 1-6 таблицы).
Найдем функции возбуждения элементарных автоматов q1 и q2. Для этой цели воспользуется матрицей переходов Т – триггера. Учитывая, что qТ1=1 qТ2=1 только в случае перехода соответствующего триггера из нулевого состояния в единичное и наоборот, заполним последние две колонки таблицы 5.
Таблица 5
|
x1(t) |
x2(t) |
Q1(t) |
Q2(t) |
Q1(t+1) |
Q2(t+1) |
qT1(t) |
qT2(t) |
|
0 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
|
0 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
|
0 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
|
0 |
1 |
1 |
1 |
0 |
1 |
1 |
0 |
|
1 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
|
1 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
|
1 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
|
1 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
|
0 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
|
0 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
Запишем функции возбуждения триггеров с применением конституент «1»:
Функции возбуждения триггеров для данного автомата не полностью определенные, так как набор входных сигналов х1=1 и х2=1 никогда не поступает. Учитывая это обстоятельство, используем для минимизации функций возбуждения триггеров диаграммы Вейча (см. рис. 8), из которых следует:
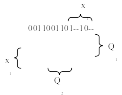
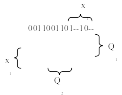
Рис. 8. Иллюстрация склеивания конституент
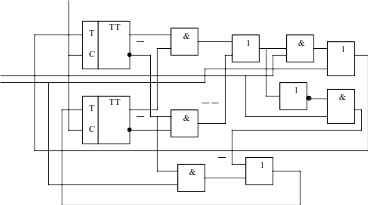Cинхронизация
qT1Q1
Q1Q2
Q1
Х1
Х2
qT2Q2
Q1Q2
Q2
x2Q1
Рис. 9. Схема синтезированного автомата с памятью
ЗАДАНИЕ 2
Тема: Непрерывно – стохастические модели (Q - схемы). Системы массового обслуживания.
Варианты заданий
Существуют следующие типы систем массового обслуживания (СМО), встречающиеся в реальных предметных областях:
- одноканальные СМО с отказами;
- многоканальные СМО с отказами;
- одноканальные СМО с ожиданием;
- многоканальные СМО с ожиданиями.
Вариант 1.
Рассчитать вероятности состояний, абсолютную и относительную пропускную способность, вероятность отказа СМО с отказами, если количество каналов n=3.
Вариант 2.
Рассчитать вероятности состояний, абсолютную и относительную пропускную способность, вероятность отказа СМО с отказами, если количество каналов n=4.
Вариант 3.
Рассчитать вероятности состояний, абсолютную и относительную пропускную способность СМО с отказами, если количество каналов n=5.
Вариант 4.
Рассчитать вероятности состояний, абсолютную и относительную пропускную способность, вероятность отказа СМО с отказами, если количество каналов n=6.
Вариант 5.
Рассчитать вероятности состояний, абсолютную и относительную пропускную способность СМО с отказами, если количество каналов n=7.
Вариант 6.
Рассчитать вероятности состояний, абсолютную и относительную пропускную способность, вероятность отказа СМО с отказами, если количество каналов n=8.
Вариант 7.
Рассчитать вероятности состояний, абсолютную и относительную пропускную способность СМО с отказами, если количество каналов n=9.
Вариант 8.
Рассчитать вероятности состояний, абсолютную и относительную пропускную способность, вероятность отказа СМО с отказами, если количество каналов n=10.
Вариант 9.
Рассчитать вероятности состояний, среднее число заявок в системе, среднюю длину очереди, вероятность обслуживания заявок в СМО с ожиданиями, если количество каналов n=2, длина очереди l=3.
Вариант 10.
Рассчитать вероятности состояний, среднее число заявок в системе, среднюю длину очереди, вероятность обслуживания заявок в СМО с ожиданиями, если количество каналов n=2, длина очереди l=4.
Вариант 11.
Рассчитать вероятности состояний, среднее число заявок в системе, среднюю длину очереди, вероятность обслуживания заявок в СМО с ожиданиями, если количество каналов n=2, длина очереди l=5.
Вариант 12.
Рассчитать вероятности состояний, среднее число заявок в системе, среднюю длину очереди, вероятность обслуживания заявок в СМО с ожиданиями, если количество каналов n=2, длина очереди l=6.
Вариант 13.
Рассчитать вероятности состояний, среднее число заявок в системе, среднюю длину очереди, вероятность обслуживания заявок в СМО с ожиданиями, если количество каналов n=3, длина очереди l=1.