Добавлен: 28.11.2018
Просмотров: 3568
Скачиваний: 53
16
Тема 2. Обеспечение заданного уровня надёжности технических
систем
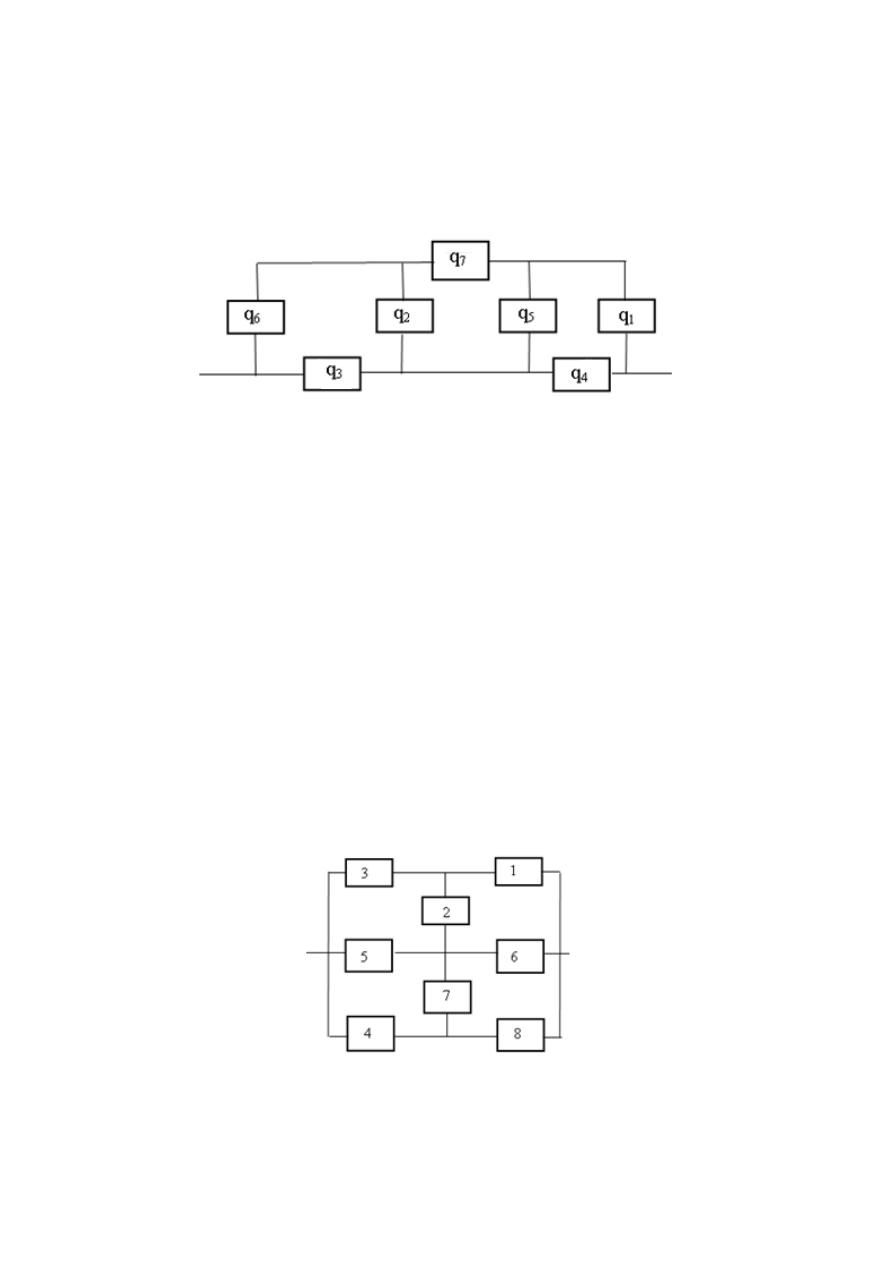
6. Структурная схема надёжности системы имеет вид «сложного
мостика», показанного на рис. 4.1.
Рис. 4.1. Структурная схема надёжности системы
Для элементов 1, 5:
4
1
,
6 10
ч ,
0,4;
t
P t
e
3, 6:
2
4
1
,
5 10
ч
t
P t
e
.
Элемент 4 имеет нормальное распределение времени безотказной рабо-
ты с параметрами
3000 ч,
100 ч;
t
t
m
элементы 2 и 7 имеют экспонен-
циальное распределение с интенсивностью
4
1
2
6 10 ч ,
5
1
7
6 10
ч .
Определите вероятность безотказной работы системы в момент
времени t = 2500 часов.
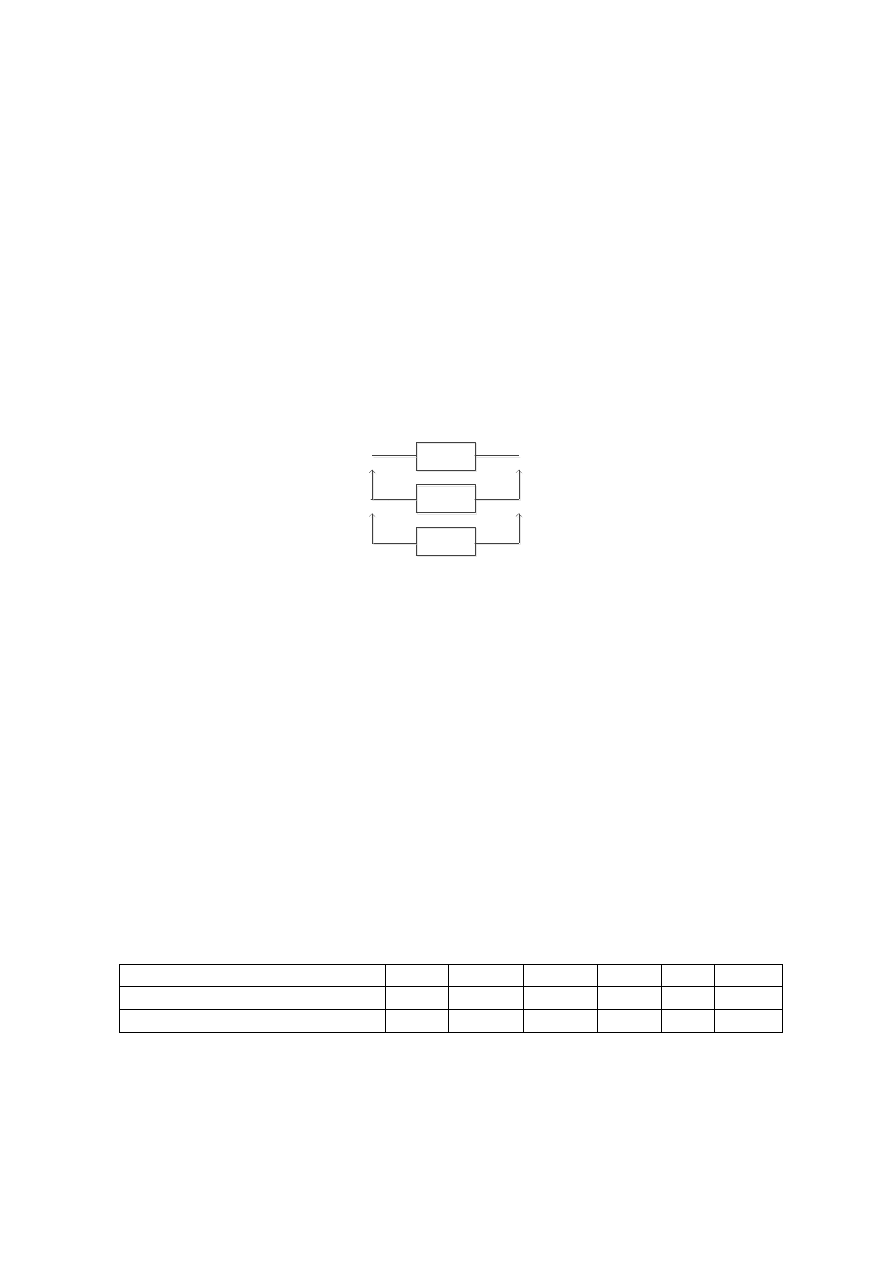
7. Найти вероятность безотказной работы за время наработки
в 200 часов системы, имеющей структурную схему надежности
(рис. 4.2), если для звеньев 1, 2, 3, 4, 5, 6
95
,
0
P
. Для звена 7 веро-
ятность безотказной работы определяется по закону Вейбулла с пара-
метрами
0,8
;
1
0,003 ч ;
для звена 8 – по закону Рэлея с пара-
метром
3
1
1,6 10
ч
.
Рис. 4.2. Структурная схема надёжности системы
17
Тема 3. Основные вопросы эксплуатационной надёжности тех-
нических систем
8. Приемник состоит из трех блоков. Интенсивности отказов этих
блоков соответственно равны:
4
1
1
( )
4 10
ч ,
t
4
1
2
( )
2,5 10
ч
t
,
4
1
3
( )
3 10
ч
t
. Требуется рассчитать вероятность безотказной ра-
боты приемника при t = 100 час для следующих случаев: а) резерв от-
сутствует; б) имеется общее дублирование приемника в целом.
9. Схема расчета надежности изделия приведена на рис. 4.3. Веро-
ятность безотказной работы нерезервированного устройства в течение
300 ч равна 0,74; интенсивность отказов устройств λ = const. Найти
вероятность безотказной работы и среднюю наработку до первого отка-
за изделия.
P
Рис. 4.3. Структурная схема надёжности системы
10. В системе имеется n основных и m резервных одинаковых
эелементов, причем все элементы постоянно включены, работают
параллельно и вероятность их безотказной работы P
i
(t) = 0,8
подчиняется экспоненциальному закону. Определить вероятность
безотказной работы системы при а) n + m = 4 и n = 3; б) n + m = 4
и n = 2; в) n + m = 4 и n = 4.
Тема 4. Диагностика автоматизированных систем
11. При испытаниях партии исполнительных механизмов (ИМ) из
6 штук было установлено, что погрешность позиционирования со време-
нем увеличивается. Данные о погрешностях, полученные для моментов
времени эксплуатации t
1
= 0 ч, t
2
= 35 + 15·N ч приведены в табл. 4.2.
Таблица 4.2
Номер ИМ
1
2
3
4
5
6
[мм] при t = 0 ч
0,19
0,13
0,17
0,13
0,09
0,15
[мм] при t = 35 + 15·N ч
0,23
0,17
0,19
0,17
0,14
0,20
Для использования ИМ в задвижках нефтепровода необходимо,
чтобы погрешность его позиционирования была ∆ ≤ 0,2 мм.

18
Полагая, что скорость изменения погрешности подчиняется нор-
мальному закону распределения, определите интервал проведения про-
филактических работ для ИМ данного типа, исключающий их посте-
пенные отказы с вероятностью
.
95
,
0
P
12. Рассчитать время проведения профилактического ремонта си-
стемы управления, имеющей значение главного параметра
5
0
X
, до-
пуск на параметр (
0,5), среднеквадратичное отклонение
23
,
0
σ
0
, ес-
ли известно, что
t
t
t
m
t
m
04
,
0
σ
)
(
σ
,
4
,
0
)
(
0
0
, а в момент начала
проведения
профилактических
работ
требуемая
вероятность
95
,
0
)
(
проф
t
P
.
13. Устройство состоит из четырёх групп элементов, в каждой из ко-
торых, соответственно, N
1
= 35, N
2
= 13, N
3
= 21, N
4
= 18 элементов с интен-
сивностями отказов
4
1
10
5
,
7
λ
ч
–1
,
4
2
10
5
,
1
λ
ч
–1
,
4
3
10
6
λ
ч
–1
,
4
4
10
5
,
2
λ
ч
–1
.
Элементы 2 и 3 групп восстанавливаемы со временем восстановле-
ния
20
τ
2
В
ч,
35
τ
3
В
ч. Пополнение элементов 1 и 4 групп в ЗИПе
проводится через 600 часов.
Определите, сколько элементов каждой группы должно быть
в ЗИПе, чтобы его достаточность была не менее 0,95?

19
Вариант 5
Тема 1. Расчет надёжности систем
1. На испытание поставлено 1000 однотипных элементов, за 3000
часов отказало 80 элементов. Требуется определить вероятность безот-
казной работы P*(t) при t = 3000 ч.
2. Определить вероятность безотказной работы и интенсивность
отказов прибора при t = 1300 часов работы, если при испытаниях полу-
чено значение среднего времени безотказной работы T = 1500 и среднее
квадратическое отклонение σ =100 ч.
3. По результатам испытания 300 приводов исполнительных меха-
низмов, проводившихся без замен и отказавших в течение 1 000 часов,
были получены данные о наработках до отказа, приведённые в табл. 5.1.
Таблица 5.1
Интервалы наработки
, ч
i
t
0–100 100–200 200–400 400–600 600–800 800–1000
Число отказов
i
n t
85
45
75
50
30
15
Вычислить значения и построить графики вероятности безотказной
работы, интенсивности отказов, частоты отказов приводов исполни-
тельных механизмов.
4. На насосной станции магистрального трубопровода установлены
3 насоса, наработка до отказа которых определяется нормальным зако-
ном распределения с параметрами:
насос 1: m
1
= 3100 ч, σ
1
= 1200 ч;
насос 2: m
2
= 2800 ч, σ
2
= 1300 ч;
насос 3: m
3
= 4400 ч, σ
3
= 2300 ч
Время безотказной работы системы управления насосами опреде-
ляется законом Рэлея с параметром λ
С
= 0,0004 ч
–1
. Определите, какова
будет вероятность безотказной работы манипулятора через неделю не-
прерывной работы в три смены?
5. Установлено, что наработка до отказа привода задвижки имеет
распределение Вейбулла с параметром α = 1,2. Вероятность безотказной
работы привода в течение наработки (0, 120) часов равна 0,92. Требует-
ся определить интенсивность отказов в момент времени t = 120 ч,
и среднюю наработку до отказа привода.
20
Тема 2. Обеспечение заданного уровня надёжности технических
систем
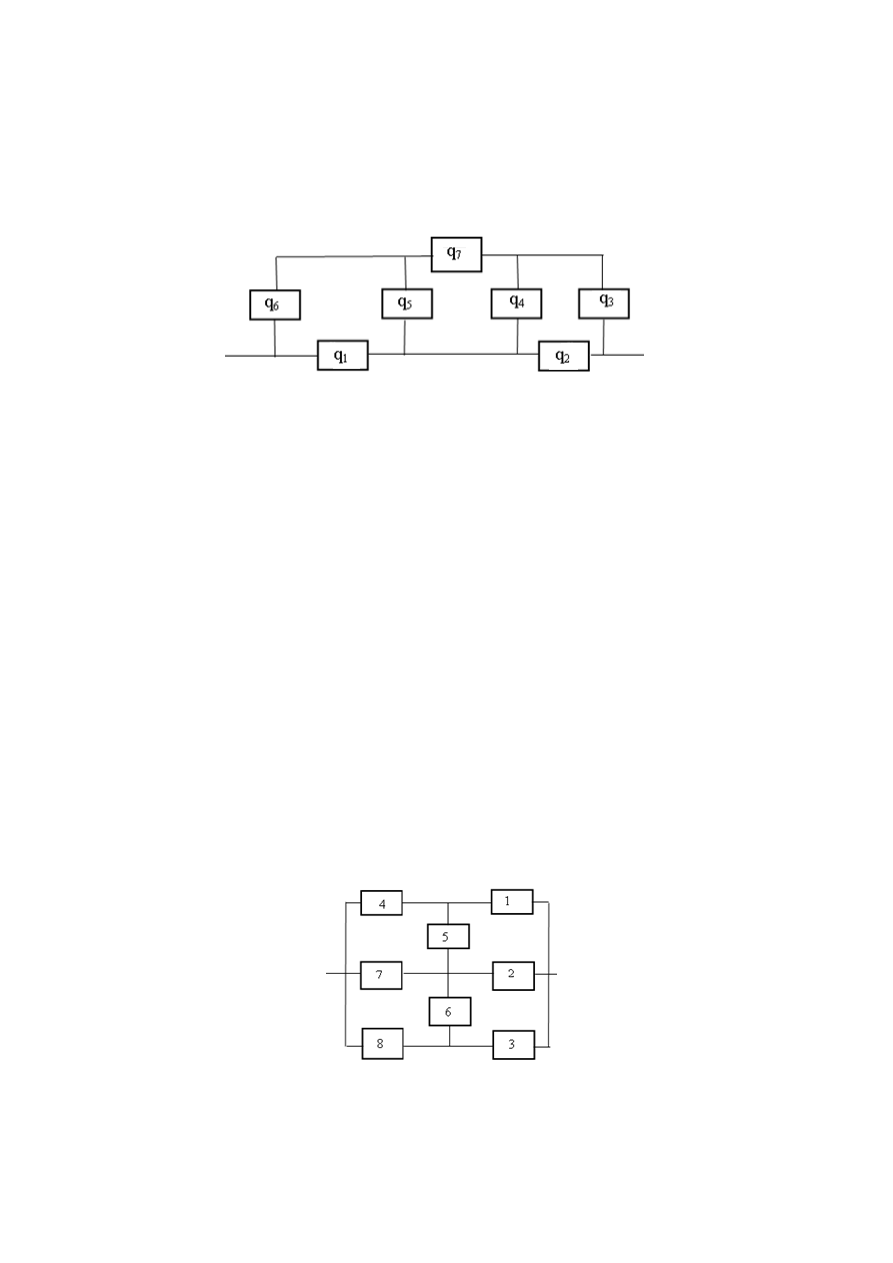
6. Структурная схема надёжности системы имеет вид «сложного
мостика», показанного на рис. 5.1.
Рис. 5.1. Структурная схема надёжности системы
Для элементов 1, 5:
4
1
,
4 10
ч ,
0,7;
t
P t
e
3, 6:
2
4
1
,
7 10
ч
t
P t
e
.
Элемент 4 имеет нормальное распределение времени безотказной
работы с параметрами
3000 ч,
100 ч;
t
t
m
элементы 2 и 7 имеют
экспоненциальное распределение с интенсивностью
4
1
2
3,5 10 ч ,
5
1
7
7,5 10
ч .
Определите вероятность безотказной работы системы в момент
времени t = 2500 часов.
7. Найти вероятность безотказной работы за время наработки
в 300 часов системы, имеющей структурную схему надежности
(рис. 5.2), если для звеньев 1, 2, 3, 4, 5, 6
95
,
0
P
. Для звена 7 веро-
ятность безотказной работы определяется по закону Вейбулла с пара-
метрами
0,4
;
1
0,003 ч ;
для звена 8 – по закону Рэлея с пара-
метром
3
1
3,8 10
ч
.
Рис. 5.2. Структурная схема надёжности системы