ВУЗ: Томский государственный университет систем управления и радиоэлектроники
Категория: Учебное пособие
Дисциплина: Дискретная математика
Добавлен: 28.11.2018
Просмотров: 10285
Скачиваний: 94
61
5
8
8
11
11
)
)
&
((
)
)
(
(
)
&
)
((
&
)
(
&
)
(
≡
∨
¬
∨
¬
≡
∨
¬
∨
∨
¬
¬
≡
≡
∨
∨
¬
¬
≡
→
∨
¬
≡
→
→
Y
X
Y
X
Y
X
Y
X
Y
X
Y
X
Y
X
Y
X
Y
X
Y
X
−
≡
∨
¬
≡
∨
¬
∨
¬
≡
∨
¬
∨
¬
≡
≡
∨
¬
∨
¬
≡
∨
¬
∨
¬
¬
∨
≡
И
И
X
Y
Y
X
Y
X
Y
Y
X
Y
И
Y
X
Y
X
X
1
4
,
3
1
)
(
)
(
))
(
&
(
))
(
&
)
((
по признаку логического следования данное рассуждение логически правиль-
но.
Третий способ проверки правильности логического рассуждения назо-
вем сокращенным, т.к. он не требует полного перебора значений переменных
для построения таблицы истинности. Для обоснования этого способа сформу-
лируем условие, при котором логическое рассуждение является неправиль-
ным. Рассуждение является неправильным, если найдется набор значений
переменных
0
0
2
0
1
,...,
,
n
X
X
X
такой, что посылка P(
0
0
2
0
1
,...,
,
n
X
X
X
) =И, а за-
ключение D(
0
0
2
0
1
,...,
,
n
X
X
X
) =Л.
Сокращенный метод заключается в следующем.
Пусть требуется проверить правильность логического следования фор-
мулы
D
из посылок
n
P
P
P
,
,
,
2
1
…
.
Предположим, что существует набор
0
0
2
0
1
,...,
,
n
X
X
X
, при котором все
посылки истинны, а заключение ложно, и попытаемся найти этот набор. Если
такой набор будет обнаружен, то наше предположение оправдалось, и рассуж-
дение является логически неправильным. Если в процессе поисков набора
придем к противоречию, то наше предположение ошибочно, а рассуждение
является логически правильным.
Пример. Проверим сокращенным способом правильность логического
рассуждения
X
Y
X
,
→
−
Y
.
Пусть существует набор
0
0
,Y
X
, при котором посылки истинны, а за-
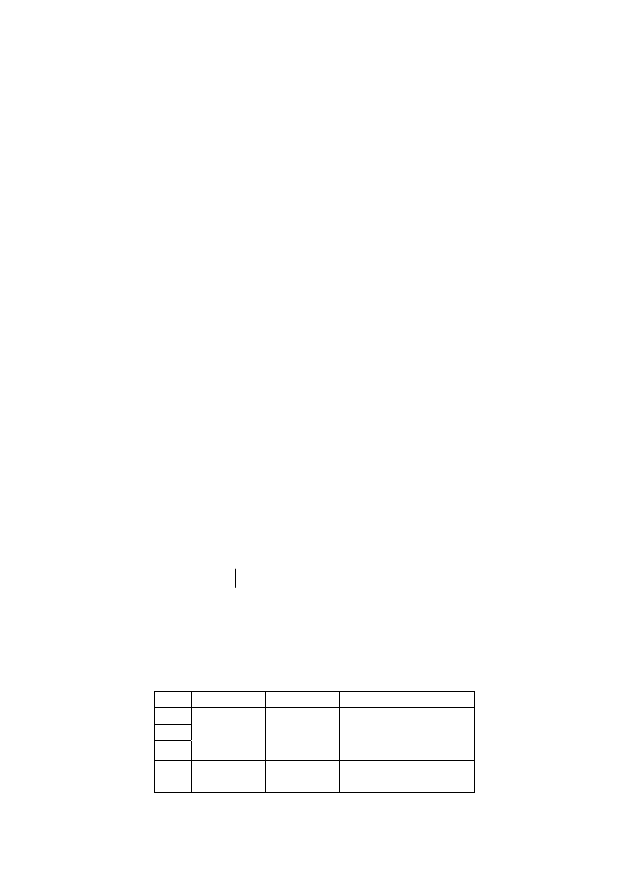
ключение ложно. Оформим это предположение в виде таблицы (табл. 2.9).
Таблица 2.9
Проверка правильности логического рассуждения
№
Истина
Ложь
Примечания
1
0
0
Y
X
→
0
X
0
Y
⎫ это
⎬ наши
⎭ предположения
2
3
4
0
0
Y
X
→
Из 2, 3 и определе-
ния импликации
62
Запишем в четвертой строке таблицы импликацию
0
0
Y
X
→
, учитывая,
что
=
0
X
И, а
=
0
Y
Л. Получим противоречие между первой и четвертой
строкой таблицы. Следовательно, рассуждение
X
Y
X
,
→
−
Y
является
ло-
гически правильным.
Если с помощью такого способа будем проверять правильность логиче-
ского рассуждения с посылками
X
P
Y
X
P
=
→
=
2
1
,
и заключением
Y
D
¬
=
, то увидим, что никакого противоречия не получается, но есть зна-
чения
=
0
X
Л,
=
0
Y
И, при которых посылки истинны, а заключение ложно.
Следовательно, это рассуждение логически неправильно.
Заметим, что не всегда сразу удается отыскать интересующий нас набор
значений переменных, и сокращенный метод приводит к частичному перебору
их значений.
Логически правильное рассуждение можно построить, пользуясь уже го-
товыми логически правильными схемами рассуждений - они называются пра-
вилами вывода (табл. 2.10).
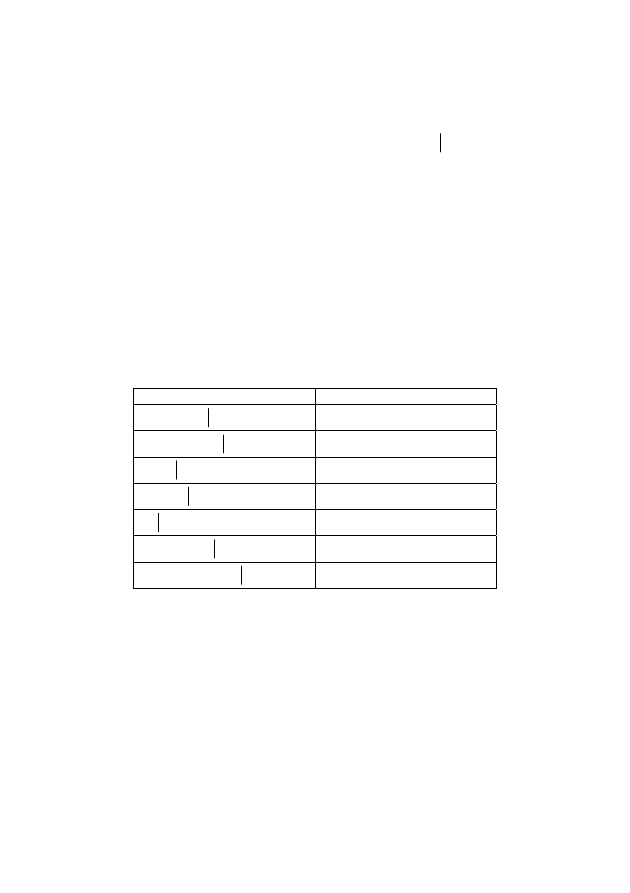
Таблица 2.10
Правила вывода
Правило
Название
A
B
A
,
→
−
B
Правило отделения (ПО)
,
A
B
→
B
A
¬ − ¬
Правило отрицания (ПТ)
B
A,
−
B
A
&
Введение конъюнкции (ВК)
B
A
&
−
A
Удаление конъюнкции (УК)
A
−
B
A
∨
Введение дизъюнкции (ВД)
B
A
∨
,
B
¬ −
A
Удаление дизъюнкции (УД)
C
B
B
A
→
→ ,
−
C
A
→
Цепное правило (ЦП)
Пример. “Если идет дождь, то кошка в комнате или в подвале. Мышка в
комнате или в норке. Если кошка в подвале, то мышка в комнате. Если кошка
в комнате, то мышка в норке, а сыр в холодильнике. Сейчас идет дождь, а сыр
лежит на столе. Где кошка и где мышка?”
Обозначим:
Д – “идет дождь”;
К – “кошка в комнате”;
Р – “кошка в подвале”;
М – “мышка в комнате”;
Н – “мышка в норке”;
Х – “сыр в холодильнике”;
¬Х – “сыр на столе”.
Получаем следующую схему рассуждения:

63
?
&
&
Х
Д
М
Р
Х
Н
К
Н
М
Р
К
Д
¬
→
→
∨
∨
→
Воспользуемся правилами вывода (табл. 2.5).
1)
X
Д
¬
&
−
Д
(УК);
2)
X
Д
¬
&
−
X
¬
(УК);
3)
Д
Р
К
Д
,
∨
→
−
Р
К
∨
(1, ПО).
Далее рассмотрим два варианта.
Вариант А. Пусть имеет место
К
. Тогда
4а)
Х
Н
К
К
&
,
→
, К
−
Х
Н &
(А, ПО);
5а)
Х
Н &
−
Х
(УК, 4а);
6а)
Х
Х ,
¬
−
Х
Х
¬
&
(2,5а) –
получили противоречие, значит, предположение было ошибочно и этот вари-
ант невозможен.
Вариант Б. Пусть имеет место
Р
. Тогда
4б)
М
Р
Р
→
,
−
М
(Б, ПО);
5б)
Р
,
М
−
М
Р &
(Б,4б,ВК).
Получено заключение
М
Р &
, т.е. “кошка в подвале, а мышка в ком-
нате”.
Таким образом, правила вывода помогают нам получить заключение из
имеющихся посылок, т.е. проводить логическое рассуждение.
2.2.3. Прямые и косвенные методы доказательств
Доказывая теоремы в математике, мы всякий раз проводим логическое
рассуждение
P
−
D
(
P
– условие теоремы,
D
– заключение), т.е. выясняем,
является ли тавтологией формула
D
P
→
. При этом доказательство теоремы
может быть прямым (как в примере с “кошкой и мышкой” в 2.2.2), когда на
основе правил вывода из посылки
P
мы получаем заключение
D
. Но доказа-
тельство может быть и косвенным, когда вместо формулы
D
P
→
мы рас-
сматриваем другую, но равносильную ей формулу.
Назовем теорему
D
P
→
прямой. Наряду с ней можно рассматривать
теоремы:

64
P
D
→
– обратную;
D
P
¬
→
¬
– противоположную;
P
D
¬
→
¬
– обратную противоположной.
Есть ли среди этих формул равносильные исходной? Построив таблицу
истинности, убеждаемся, что есть (табл. 2.11).
Таблица 2.11
Таблица истинности
P D
D
P
→
P
D
→
D
P
¬
→
¬
P
D
¬
→
¬
И
И
И
И
И
И
И
Л
Л
И
И
Л
Л
И
И
Л
Л
И
Л
Л
И
И
И
И
Прямая теорема равносильна обратно противоположной:
P
D
D
P
¬
→
¬
≡
→
.
Эта равносильность имеет специальное название – закон контрапози-
ции. Заметим, что обратная и противоположная теоремы также связаны зако-
ном контрапозиции.
Пример. Вместо доказательства утверждения “Если
n
m
⋅
нечетное чис-
ло, то
m
и
n
нечетны” (
D
P
→
) согласно закону контрапозиции можно дока-
зывать утверждение (
P
D
¬
→
¬
): “Если хотя бы одно из чисел
m
или
n
чет-
но, то
n
m
⋅
четно”.
К методам косвенного доказательства относятся доказательства “от про-
тивного”. Схемы таких доказательств основаны на равносильностях (справед-
ливость которых можно проверить по таблице истинности):
A
B
A
B
A
¬
→
¬
≡
→
)
&
(
;
B
B
A
B
A
→
¬
≡
→
)
&
(
;
C
C
B
A
B
A
¬
→
→
¬
≡
→
&
)
(
.
2.2.4. Решение задачи контрольной работы №2
Задача. Проверить правильность логического рассуждения сокращенным
способом. Какими еще способами можно решить эту задачу?
“Если сегодня будет мороз, то я пойду на каток. Если сегодня будет от-
тепель, то я пойду на дискотеку. Сегодня будет мороз или оттепель. Следова-
тельно, я пойду на дискотеку”.
Решение. Формализуем условие задачи, введя обозначения:
М – “сегодня будет мороз”;
К – “я пойду на каток”;
О – “сегодня будет оттепель”;
Д – “я пойду на дискотеку”.
Схема рассуждения имеет вид:

65
Д
О
М
Д
О
К
М
∨
→
→
Рассуждение является логически правильным, если при любых наборах
значений переменных (
М, К, О, Д
), для которых все посылки истинны, за-
ключение
также
истинно.
Предположим
противное:
есть
набор
(
0
0
0
0
,
,
,
Д
О
К
М
) такой, что посылки истинны, а заключение ложно (табл.
2.12). Применяя определения логических операций, попытаемся найти этот
набор.
Таблица 2.12
Проверка правильности логического рассуждения
№
Истина
Ложь
Примечания
1
М
0
→К
0
О
0
→Д
0
М
0
∨О
0
Д
0
предполагаем,
что посылки истинны,
а заключение ложно
2
3
4
5
М
0
К
0
О
0
из 2, 4 и определения импликации
из 3, 5 и определения дизъюнкции
из 1, 6 и определения импликации
6
7
Убеждаемся, что предположение справедливо при значениях перемен-
ных
=
0
М
И,
=
0
К
И,
=
0
О
Л,
=
0
Д
Л. Следовательно, рассуждение не явля-
ется логически правильным.
Другой способ решения задачи: построить таблицу истинности для фор-
мулы
Д
О
М
Д
О
К
М
→
→
→
→
)
(
&
)
(
&
)
(
и убедиться, что она не явля-
ется тавтологией. Тогда по признаку логического следования (см. 2.2.2) рас-
суждение не является логически правильным. Так как в рассуждении участву-
ют четыре высказывательных переменные (
М, К, О, Д
), то таблица истинно-
сти будет содержать
16
2
4
=
строк, и этот способ является трудоемким.
С помощью правил вывода можно построить логически правильное рас-
суждение, но не всегда можно доказать неправильность логического рассуж-
дения.
Поэтому для данной задачи наиболее удобным является сокращенный
способ проверки правильности логического рассуждения.