ВУЗ: Томский государственный университет систем управления и радиоэлектроники
Категория: Учебное пособие
Дисциплина: Дискретная математика
Добавлен: 28.11.2018
Просмотров: 10283
Скачиваний: 94

66
2.2.5. Контрольные вопросы и упражнения
1.
Что означает предложение: ”Из формулы
P
логически следует фор-
мула
D
”?
2.
Покажите по определению, что из формулы
X
P
=
логически сле-
дует формула
Y
X
D
∨
=
.
3.
Покажите, что из посылок
Y
X
P
→
=
1
и
X
P
¬
=
2
не следует ло-
гически формула
Y
D
¬
=
.
4.
Запишите в виде схемы следующее рассуждение: ”Если идет дождь,
то я беру зонт. Если светит солнце, то я беру веер. Идет дождь или светит
солнце. Следовательно, я беру зонт или веер”.
5.
Перечислите способы, которыми можно доказать правильность ло-
гического рассуждения.
6.
Обоснуйте сокращенный способ проверки правильности логическо-
го рассуждения.
7.
Для чего применяются правила вывода?
8.
Докажите справедливость цепного правила вывода (табл. 2.10).
9.
Сформулируйте теорему Пифагора и обратно противоположную к
ней.
10.
Приведите примеры косвенных доказательств теорем.
2.3. Логика предикатов
2.3.1. Понятие предиката
Не всякие логические рассуждения могут быть проведены средствами
логики высказываний. Иногда нам требуется исследовать саму структуру
предложений. Это можно сделать с помощью логики предикатов. Предложе-
ние “
x
белого
цвета” не является высказыванием, но если вместо
x
подставить
конкретное значение, например “ снег” или “жираф”, получим высказывание.
Это предложение описывает свойство
x
“быть белого цвета” и является одно-
местным предикатом. Если рассмотрим предложение “
x
больше ростом, чем
y
”, то подставляя конкретные пары значений
)
,
(
y
x
, будем получать высказы-
вания, принимающие значение “истина” или “ложь”. Это предложение описы-
вает свойство пары объектов и является двухместным предикатом.
В общем случае
n-
местным предикатом
)
,
,
,
(
2
1
n
x
x
x
P
…
называется
функция, аргументы которой являются элементами произвольного множества
M
, а значения принадлежат множеству {И, Л}, т.е.
→
n
n
M
x
x
x
P
:
)
,
,
,
(
2
1
…
{И, Л}. Элементы множества
M
называются предметными переменными. Ко-
личество предметных переменных есть порядок (местность) предиката. Мно-
жество значений предметных переменных, на котором предикат принимает
значение И, называется множеством истинности предиката. Например,
определим на множестве
M=
N
одноместный предикат
)
(
x
С
– “
x
делится на

67
2”. Его множеством истинности является множество целых положительных
чисел. На множестве
M=
R
зададим двухместный предикат
)
,
(
y
x
L
– “
x
меньше
y
”. Его множество истинности можно изобразить на плоскости
xOy
как множество точек, лежащих выше прямой
y
x
=
.
Пусть два предиката
P
и
Q
определены на одном и том же множестве
M
.
Так как предикаты могут принимать только два значения (истина или ложь), то
к ним можно применить операции логики высказываний, образуя новые пре-
дикаты, при этом порядок (местность) предиката не меняется:
Q
P
Q
P
Q
P
Q
P
P
↔
→
∨
¬
,
,
,
&
,
.
В качестве упражнения дайте опре-
деление этим предикатам самостоятельно.
2.3.2. Кванторы
Кроме операций логики высказываний, в логике предикатов рассматри-
ваются операции квантификации. Для их обозначения используются символы:
∀ - квантор всеобщности;
∃ - квантор существования.
Рассмотрим эти операции вначале для одноместных предикатов.
Пусть
)
(
x
P
– одноместный предикат, определенный на множестве
M
.
Тогда под выражением
)
(
x
xP
∀
будем понимать высказывание, которое при-
нимает значение истина тогда и только тогда, когда
)
(
x
P
истинно для каждо-
го элемента
x
множества
M
. Это высказывание уже не зависит от
x
. Перемен
-
ную
x
в предикате
)
(
x
P
называют свободной, а в высказывании
)
(
x
xP
∀
–
связанной квантором всеобщности.
Аналогично, под выражением
)
(
x
xP
∃
понимают высказывание, которое
является истинным, если найдется хотя бы один элемент
x
множества
M
, для
которого
)
(
x
P
истинно, и ложным, если ни одного такого элемента во множе-
стве M нет. Высказывание
)
(
x
xP
∃
не зависит от
x
, в нем переменная
x
связана
квантором существования.
Операции квантификации являются обобщением операций конъюнкции
и дизъюнкции на случай бесконечного множества
M
предметной переменной.
Действительно, пусть множество
M
конечно:
}
,
,
,
{
2
1
n
x
x
x
M
…
=
. Тогда
=
∀
)
(
x
xP
И означает, что для всех элементов множества
M
выполняется
свойство
P
, т.е.
.
)
(
&
...
&
)
(
&
)
(
)
(
&
2
1
1
И
x
P
x
P
x
P
x
P
n
i
n
i
=
=
=
Равенство
=
∀
)
(
x
xP
Л означает, что найдется хотя бы один элемент
M
x
m
∈
такой, что
=
)
(
m
x
P
Л, т.е.
.
)
(
&
1
Л
x
P
i
n
i
=
=

68
Операция квантификации понижает порядок (местность) предиката, а
одноместный предикат превращает в высказывание ( 0-местный предикат).
Применение одной кванторной операции к двухместному предикату пре-
вращает его в одноместный предикат:
)
,
(
y
x
yL
∃
– здесь связана переменная
y
,
а переменная
x
осталась свободной; а двух – в высказывание
)
,
(
y
x
yL
x
∃
∀
–
“для любого
x
найдется y такой, что
y
x
<
” (если предикат
)
,
(
y
x
L
означает
“
y
x
<
”). Если на двухместный предикат навешивают два одноименных кван-
тора, то их можно менять местами, если же кванторы разноименные, то этого
делать нельзя.
Пример. Пусть предикат
)
,
(
y
x
P
выражает свойство “покупателю
x
подходит по размеру пара ботинок
y
”. Тогда высказывание
)
,
(
y
x
yP
x
∃
∀
мо-
жет служить рекламой обувного магазина: “каждому покупателю мы подберем
подходящую по размеру пару ботинок”, а высказывание
)
,
(
y
x
xP
y
∀
∃
– нет
(“у нас есть пара ботинок, подходящая по размеру любому покупателю”).
2.3.3. Формулы логики предикатов
Из предикатных символов с помощью знаков логических операций и
кванторов строятся формулы логики предикатов, которые используются в ин-
формационных задачах для описания предметной области. При этом определя-
ется содержание множества предметных переменных
M
, а каждому предикат-
ному символу придается смысл – задается свойство, которое описывает этот
предикат. Таким образом, формулам придается некоторая интерпретация.
Одна и та же формула в разных интерпретациях может иметь разные значения.
Пример. Пусть задана формула
)
,
(
y
x
yP
x
F
∀
∃
=
. Рассмотрим две ее
интерпретации:
I
1
:
M=
N
,
"
"
)
,
(
y
x
y
x
P
≤
−
;
I
2
:
M=
Z
,
"
"
)
,
(
y
x
y
x
P
≤
−
.
В первом случае
F=
И – это утверждение о существовании наименьшего
натурального числа. Во втором случае
F=
Л.
Если формула
F
истинна при любых значениях своих аргументов в неко-
торой интерпретации, то она называется истинной в данной интерпретации.
Формула, истинная в любой интерпретации, называется общезначимой.
Например, формула
)
(
)
(
y
A
x
xA
F
→
∀
=
общезначима. Аналогично, можно
говорить о формулах равносильных в данной интерпретации и просто равно-
сильных.
В логике высказываний мы всегда можем определить по таблице истин-
ности, является ли формула тавтологией. В логике предикатов нет единой
процедуры, позволяющей определить, является ли формула общезначимой:
ведь каждой формуле можно придать бесконечное число интерпретаций.
2.3.4. Равносильные преобразования формул

69
Две формулы логики предикатов называются равносильными, если они
принимают одинаковые истинностные значения при любых значениях пере-
менной в любой интерпретации. Все равносильности логики высказываний
(табл. 2.5) справедливы в логике предикатов. Кроме этого, в логике предикатов
есть равносильности, связанные с преобразованиями формул, содержащих
кванторы (табл. 2.13).
Таблица 2.13
Основные равносильности логики предикатов
№
Формула
1
))
(
(
))
(
(
x
P
x
x
xP
¬
∀
≡
∃
¬
2
))
(
(
))
(
(
x
P
x
x
xP
¬
∃
≡
∀
¬
3
))
(
&
)
(
(
))
(
(
&
))
(
(
x
Q
x
P
x
x
xQ
x
xP
∀
≡
∀
∀
4
))
(
)
(
(
))
(
(
))
(
(
x
Q
x
P
x
x
xQ
x
xP
∨
∃
≡
∃
∨
∃
5
))
(
)
(
(
))
(
(
))
(
(
y
Q
x
P
y
x
x
xQ
x
xP
∨
∀
∀
≡
∀
∨
∀
6
))
(
&
)
(
(
))
(
(
&
))
(
(
y
Q
x
P
y
x
x
xQ
x
xP
∃
∃
≡
∃
∃
Докажем первую из этих формул:
))
(
(
))
(
(
x
P
x
x
xP
¬
∀
≡
∃
¬
.
Зададим произвольную интерпретацию I этой формулы на множестве
M
.
Покажем, что левая и правая части формулы принимают одинаковые значения
при любых значениях предметной переменной
M
x
∈
.
Пусть
=
∃
¬
))
(
(
x
xP
И в данной интерпретации, тогда
=
∃
)
(
x
xP
Л. По
определению квантора существования это означает, что во множестве
M
нет
такого элемента
x
, для которого
)
(
x
P
принимает значение “истина”. Следова-
тельно, при всех значениях предметной переменной
x
предикат
≡
)
(
x
P
Л, а
≡
¬
)
(
x
P
И. По определению квантора всеобщности формула
))
(
(
x
P
x
¬
∀
истинна в данной интерпретации.
Если же формула
))
(
(
x
xP
∃
¬
ложна в данной интерпретации, тогда
)
(
x
xP
∃
истинна. Это значит, что найдется хотя бы один элемент
M
a
∈
та-
кой, что
=
)
(
a
P
И, т.е.
=
¬
)
(
a
P
Л. Но тогда
))
(
(
x
P
x
¬
∀
ложна в данной ин-
терпретации.
Следовательно,
))
(
(
x
xP
∃
¬
и
))
(
(
x
P
x
¬
∀
равносильны в данной ин-
терпретации, а в силу ее произвольности, равносильны.
Остальные равносильности логики предикатов (табл. 2.7) доказываются
аналогично. Обратите внимание на разницу между парами формул 3, 4 и 5, 6.
В формулах 3, 4 используются “родственные” операции: конъюнкция и кван-
тор всеобщности, дизъюнкция и квантор существования. В формулах 5, 6,
прежде чем выносить квантор за скобки, нам приходится делать замену пере-
70
менной:
))
(
(
&
))
(
(
))
(
(
&
))
(
(
y
yQ
x
xP
x
xQ
x
xP
∃
∃
≡
∃
∃
, чтобы подчеркнуть
разные области действия кванторов существования.
Действительно, если
)
(
x
P
означает “
x
получил пятерку по математике”,
а
)
(
x
Q
– “
x
получил пятерку по физике”, то может оказаться, что
=
∃
∃
))
(
(
&
))
(
(
x
xQ
x
xP
И, а
=
∃
))
(
&
)
(
(
(
x
Q
x
P
x
Л (если пятерки получили
разные люди).
2.3.5. Рассуждения в логике предикатов
Рассмотрим рассуждение: “Каждый орел умеет летать. Некоторые свиньи
не умеют летать. Следовательно, некоторые свиньи – не орлы”. На языке пре-
дикатов его можно записать так:
))
(
&
)
(
(
))
(
&
)
(
(
))
(
)
(
(
x
O
x
S
x
x
L
x
S
x
x
L
x
O
x
¬
∃
¬
∃
→
∀
Здесь предикат
)
(
x
O
описывает свойство
x
быть орлом,
)
(
x
S
– быть
свиньей,
)
(
x
L
– уметь летать. С каждым предикатом связано множество ис-
тинности.
Условие
))
(
)
(
(
x
L
x
O
x
→
∀
∀x
означает, что
L
O
⊆
;
))
(
&
)
(
(
x
L
x
S
x
¬
∃
– что
≠
¬
∩ L
S
∅
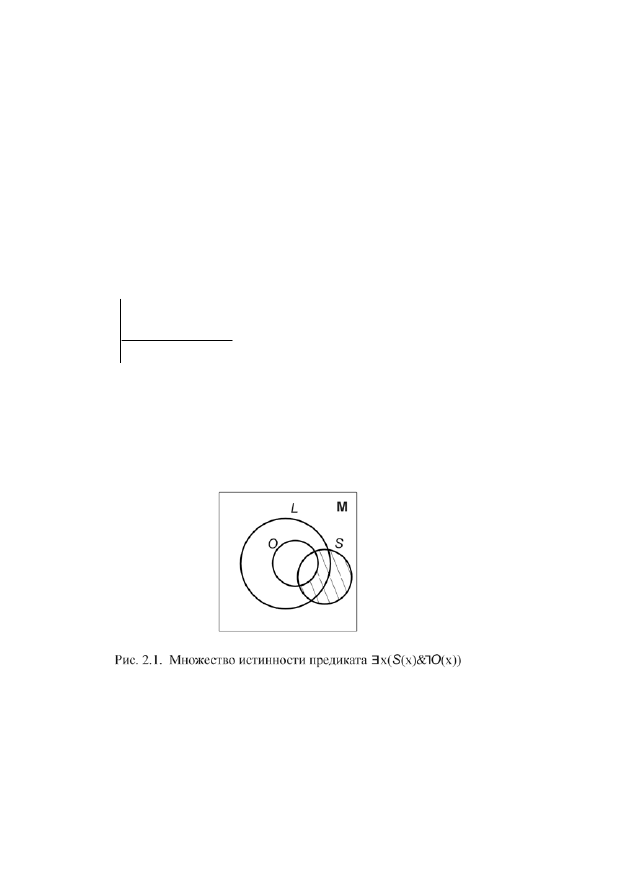
;
))
(
&
)
(
(
x
O
x
S
x
¬
∃
– что
≠
¬
∩ O
S
∅
(рис. 2.1).
В этом рассуждении мы проверили правильность логического рассужде-
ния, опираясь на геометрическую иллюстрацию. В логике предикатов суще-
ствуют формальные методы проверки правильности рассуждений. Они ис-
пользуют специальную форму записи формулы логики предикатов – предва-
ренную нормальную форму (ПНФ). Записать формулу в предваренной нор-
мальной форме – это значит:
1)
перейти от символов
→ и ~ к символам &, ∨, ¬;