ВУЗ: Томский государственный университет систем управления и радиоэлектроники
Категория: Учебное пособие
Дисциплина: Дискретная математика
Добавлен: 28.11.2018
Просмотров: 10286
Скачиваний: 94

51
__________ = ________________________ .
4.
Количество сочетаний из
n
элементов по
r
элементов определяется
по формуле
____________ = ________________________ .
5.
Сформулируйте основные правила комбинаторики.
6.
Сколькими способами можно выбрать конверт и марку для письма,
если имеется 5 конвертов и 4 марки?
7.
Сколько пятизначных номеров можно составить из девяти цифр
{1,2,3,4,5,6,7,8,9}?
8.
Сколькими способами можно составить трехцветный полосатый флаг
(все полосы горизонтальные), если имеются ткани пяти различных цветов?
9.
Сколькими способами могут расположиться в турнирной таблице 7
футбольных команд, если известно, что все команды набрали различное коли-
чество очков?
10.
Сколькими способами можно составить команду из 4 человек, если
имеется 7 бегунов?
11.
Сколькими способами можно разложить 12 различных предметов по
четырем различным ящикам так, чтобы в каждом ящике оказалось по три
предмета?
12.
Сколькими способами можно разложить 6 одинаковых шаров по че-
тырем различным ящикам?
13.
Запишите разложение бинома
5
)
(
b
a
−
.
14.
Докажите свойство симметрии биномиальных коэффициентов, срав-
нив формулы для
k
n
С
и
k
n
n
С
−
.
15.
Найдите максимальный числовой коэффициент в разложении бинома
8
)
1
(
x
+
.

52
2. ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОЙ ЛОГИКИ
2.1. Логика высказываний
2.1.1. История математической логики
Логика как наука о законах человеческого мышления зародилась в дав-
ние времена. Родоначальником формальной логики считают Аристотеля (IV в.
до н.э.). До сих пор мы пользуемся классификацией суждений, введенной этим
древнегреческим ученым, именно он впервые обратил внимание на то, что
рассуждения мы проводим, исходя из структуры утверждений, а не из их кон-
кретного содержания.
В конце семнадцатого века вопросы логики привлекли внимание немец-
кого ученого Г. Лейбница (1646-1716 гг.). Он считал, что логика должна стать
“искусством вычисления”. Основные понятия должны быть обозначены осо-
быми символами, должны быть выработаны правила их соединения, и тогда
всякое рассуждение можно будет заменить вычислением. Эти идеи были ча-
стично реализованы в работах английского ученого Дж. Буля (1815-1864 гг.).
Он создал алгебру высказываний (впоследствии ее стали называть алгеброй
логики). Работа Буля стала началом развития математической логики (а ари-
стотелеву логику называют традиционной формальной логикой).
В конце XIX века логика нашла применение в обосновании основных
понятий и идей математики. Для построения математической теории исполь-
зуется аксиоматический способ: без доказательств принимаются основные
понятия этой теории (аксиомы), из которых логически выводится все ее со-
держание. Логическими средствами этого являются правила вывода данной
теории.
В начале двадцатого века математическая логика нашла применение в
технике, затем была установлена тесная связь математической логики с новой
наукой – кибернетикой. Как часть математической логики возникла новая ма-
тематическая дисциплина – теория алгоритмов, занимающаяся проблемами
обоснования существования алгоритмов решения задач.
2.1.2. Понятие высказывания
Изучая теорию множеств, мы не давали строго определения понятия
“множество”, считая его понятием неопределяемым, первичным; однако, при
этом мы опирались на интуитивное представление о понятии “множество”.
Так же поступим и при изучении математической логики: не будем давать
строгого определения понятия “высказывание”, считая высказыванием любое
повествовательное предложение, о котором есть смысл говорить, что оно ис-
тинно или ложно. При этом высказывание не может быть одновременно и ис-
тинным, и ложным. Например, “
3
2
2
=
+
” – высказывание, принимающее
значение “ложь” (Л), “
7
5
2
=
+
” – высказывание, принимающее значение
“истина” (И), а “
4
=
+ y
x
” не является высказыванием.

53
2.1.3. Операции над высказываниями
В естественном языке из нескольких простых предложений можно соста-
вить сложное, пользуясь союзами “и”, “или” и т.п. Так же из простых выска-
зываний (высказывательных переменных) будем строить составные, пользуясь
логическими союзами – логическими операциями.
Отрицанием (инверсией) высказывания
X
называется высказывание, ис-
тинное тогда и только тогда, когда
X
ложно (обозначается
X
¬
или
X
, чита-
ется “не
X
” или “неверно, что
X
”).
Конъюнкцией
Y
X &
двух высказываний называется высказывание, ис-
тинное тогда и только тогда, когда истинны оба высказывания
X
и
Y
. Эта ло-
гическая операция соответствует соединению высказываний союзом ”и”.
Дизъюнкцией
Y
X
∨
двух высказываний
X
и
Y
называется высказыва-
ние ложное в том и только в том случае, когда оба высказывания
X
и
Y
ложны.
В разговорной речи этой логической операции соответствует союз “или” (не-
исключающее “или”).
Импликацией двух высказываний
X
и
Y
называется высказывание, лож-
ное тогда и только тогда, когда
X
истинно, а
Y
– ложно (обозначается
Y
X
→
; читается “
X
влечет
Y
”, “если
X
, то
Y
”). Операнды этой операции
имеют специальные названия:
X
– посылка,
Y
– заключение.
Эквиваленцией двух высказываний
X
и
Y
называется высказывание, ис-
тинное тогда и только тогда, когда истинностные значения
X
и
Y
одинаковы
(обозначение:
Y
X
Y
X
↔
,
~
).
2.1.4. Таблицы истинности
Операнды логических операций могут принимать только два значения: И
или Л. Поэтому каждую логическую операцию
¬, &, ∨, →, ↔ легко задать с
помощью таблицы, указав значение результата операции в зависимости от
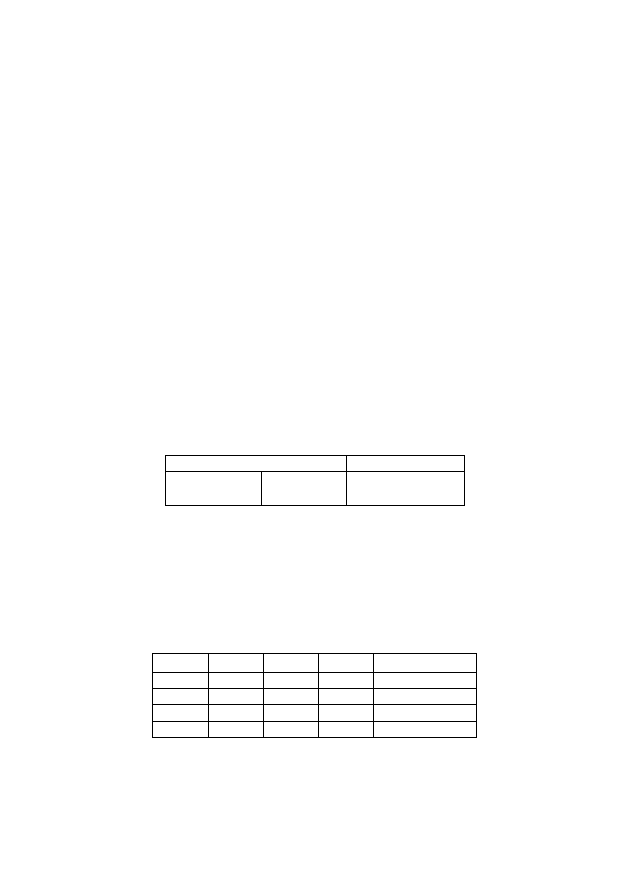
значений операндов. Такая таблица называется таблицей истинности
(табл. 2.1).
Таблица 2.1
Таблицы истинности логических операций
X
Y
¬ X
X&Y
X
∨Y X→Y X↔Y
И
И
Л
И
И
И
И
И
Л
Л
Л
И
Л
Л
Л
И
И
Л
И
И
Л
Л
Л
И
Л
Л
И
И
54
2.1.5. Формулы логики высказываний
В алфавит логики высказываний входят две специальные буквы И и Л,
обозначающие логические константы “истина” и “ложь”, прописные буквы
для обозначения высказывательных переменных, знаки логических операций и
круглые скобки. С помощью этих символов мы строим формулы логики вы-
сказываний, заключая каждую операцию в скобки:
)
(
)
))
(
&
(((
A
C
B
A
F
¬
∨
→
¬
=
.
Чтобы формулы не были громоздкими, договоримся опускать некоторые
скобки, учитывая приоритет логических операций (“силу” связок). В табл. 2.1
логические операции записаны в порядке убывания приоритета. Учитывая эту
договоренность, вышеприведенную формулу можно записать короче:
A
C
B
A
F
¬
∨
→
¬
=
)
&
(
.
В логике высказываний особую роль играют формулы, принимающие
значение “истина” при любых значениях переменных. Такие формулы назы-
ваются тавтологиями (или тождественно истинными формулами). Формулы,
принимающие значение “истина” хотя бы при одном наборе списка перемен-
ных, называются выполнимыми. Формулы, принимающие значение “ложь”
при любых значениях переменных, называются противоречиями (тожде-
ственно ложными, невыполнимыми) (табл. 2.2).
Таблица 2.2
Формулы логики высказываний
Выполнимые формулы
Невыполнимые
Тавтологии
≡
¬
∨ X
X
И
Остальные
Y
X
¬
→
Противоречия
≡
¬X
X &
Л
В логике высказываний всегда можно определить, является ли данная
формула тавтологией – для этого достаточно построить ее таблицу истинно-
сти.
Пример: Является ли тавтологией формула
X
Y
X
F
¬
→
→
=
)
(
?
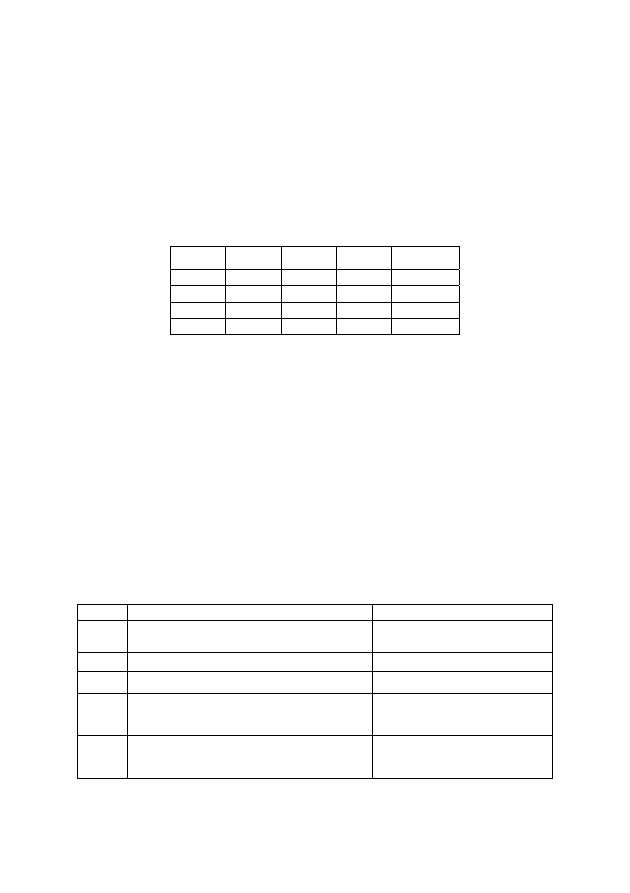
Построим таблицу истинности для формулы
F
(табл. 2.3).
Таблица 2.3
Таблица истинности
X Y
X
→Y
¬ X
(
X
→Y)→ ¬ X
И
И
И
Л
Л
И
Л
Л
Л
И
Л
И
И
И
И
Л
Л
И
И
И
Формула принимает значение “ложь” на наборе переменных
X
=И,
Y
=Л,
следовательно, не является тавтологией; это выполнимая формула.
55
2.1.6. Равносильные преобразования формул
Формулы
1
F
и
2
F
называются равносильными, если они принимают
одинаковые истинностные значения при любых значениях своих переменных.
Пример.
Покажем
равносильность
формул
Y
X
F
→
=
1
и
Y
X
F
∨
¬
=
2
. Для этого составим таблицу истинности (табл. 2.4).
Таблица 2.4.
Таблица истинности
X Y
¬X
1
F
2
F
И
И
Л
И
И
И
Л
Л
Л
Л
Л
И
И
И
И
Л
Л
И
И
И
Сравнивая два последних столбца таблицы, убеждаемся, что они полно-
стью совпадают, т.е.
2
1
F
F
≡
.
Очевидно, что равносильны любые две тождественно истинные форму-
лы, равносильны любые две тождественно ложные формулы.
Отношение равносильности на множестве формул логики высказываний
является отношением эквивалентности, так как обладает свойствами рефлек-
сивности (
F
F
≡
для любой формулы
F
), симметричности (если
2
1
F
F
≡
, то
1
2
F
F
≡
), транзитивности (если
2
1
F
F
≡
и
3
2
F
F
≡
, то
3
1
F
F
≡
). С помо-
щью этого отношения все множество формул логики высказываний разбивает-
ся на классы равносильных формул.
Основные равносильности (табл. 2.5) – законы логики высказываний -
доказываются с помощью таблиц истинности.
Таблица 2.5
Основные равносильности логики высказываний
№
Формула
Название
1
И
≡
¬
∨ X
X
Закон исключенного треть-
его
2
Л
&
≡
¬X
X
Закон противоречия
3
X
Y
Y
X
X
Y
Y
X
∨
≡
∨
≡
,
&
&
Законы коммутативности
4
)
&
(
&
&
)
&
(
Z
Y
X
Z
Y
X
≡
)
(
)
(
Z
Y
X
Z
Y
X
∨
∨
≡
∨
∨
Законы ассоциативности
5
)
&
(
)
&
(
)
(
&
Z
X
Y
X
Z
Y
X
∨
≡
∨
)
(
&
)
(
)
&
(
Z
X
Y
X
Z
Y
X
∨
∨
≡
∨
Законы дистрибутивности