ВУЗ: Томский государственный университет систем управления и радиоэлектроники
Категория: Учебное пособие
Дисциплина: Дискретная математика
Добавлен: 28.11.2018
Просмотров: 10279
Скачиваний: 94

76
3.
Какая дуга орграфа называется петлей?
4.
Что такое множество достижимости вершины
x
?
5.
Что такое множество контрдостижимости вершины
x
?
6.
Какую особенность имеет орграф рефлексивного отношения?
7.
Какую особенность имеет орграф симметричного отношения?
8.
В орграфе 6 вершин и 8 дуг. Какую размерность имеет его матрица
смежности? А матрица инцидентности?
3.2. Неориентированные графы
3.2.1. Основные термины
Неориентированным графом (неорграфом) называется упорядоченная
пара
)
,
(
U
X
G
=
, где
X
– множество вершин неорграфа
G
, а
U
– множество
неупорядоченных пар вершин (ребер неорграфа). Любые две вершины неор-
графа могут быть соединены не более, чем одним ребром. Две вершины назы-
ваются смежными, если они соединены ребром. Два ребра называются смеж-
ными, если они имеют общую вершину. Вершина инцидентна ребру (ребро
инцидентно вершине), если она является одним из концов ребра. Степень
)
(x
p
вершины
x
равна количеству ребер, инцидентных вершине
x
. Сумма
степеней всех вершин неорграфа
)
,
(
U
X
G
=
равна удвоенному числу ребер:
.
2
)
(
U
x
p
X
x
⋅
=
∑
∈
Неорграф называется пустым (обозначается
n
O
), если все вершины
имеют нулевые степени (рис. 3.3, а). Неорграф называется полным (обознача-
ется
n
K
), если все его вершины смежны друг другу (рис. 3.3, б). Неорграф
называется двудольным, если множество его вершин можно разбить на два
непустых подмножества
1
X
и
2
X
так, что смежные вершины принадлежат
разным подмножествам (рис. 3.3, в). Полный двудольный граф такой, что
r
X
s
X
=
=
2
1
,
, обозначается
r
s
K
,
(рис. 3.3, г).
В дальнейшем везде вместо термина “неорграф” будем говорить “граф”.

77
Граф
)
,
(
1
1
1
U
X
G
=
называется подграфом графа
)
,
(
U
X
G
=
, если
U
U
X
X
⊆
⊆
1
1
,
. Подграф
)
,
(
1
1
1
U
X
G
=
называется остовным подграфом
графа
)
,
(
U
X
G
=
, если
X
X
=
1
. На рис. 3.4, б, в приведены остовные под-
графы графа
G
(рис. 3.4, а).
3.2.2. Матрицы графа
Пусть
)
,
(
U
X
G
=
неорграф, причем
m
X
n
X
=
=
2
1
,
. Присвоим номе-
ра вершинам графа:
}
,
,
,
{
2
1
n
x
x
x
X
…
=
.
Матрицей смежности графа
G
называется квадратная матрица
A
раз-
мерности
n
n
×
(
n
строк,
n
столбцов), элементы которой
⎩
⎨
⎧
∉
=
,
}
,
{
,
0
,
,
1
U
x
x
если
x
вершине
смежна
x
вершина
если
a
j
i
j
i
ij
.
,
1
,
n
j
i
=
Матрица смежности неорграфа обладает двумя особенностями: а) на
главной диагонали матрицы могут стоять только нули:
n
i
a
ii
,
1
,
0
=
=
, т.к. в
неорграфе нет петель; б) матрица симметрична относительно главной диаго-
нали:
n
j
i
a
a
ji
ij
,
1
,
,
=
=
, т.к. ребро является неупорядоченной парой вершин.
Занумеруем теперь и ребра графа:
}
,
,
,
{
2
1
m
u
u
u
U
…
=
.
Матрицей инцидентности графа
G
называется прямоугольная матрица
B
размерности
m
n
×
(
n
строк,
m
столбцов), элементы которой
⎩
⎨
⎧
=
.
,
,
0
,
,
1
ны
неинцидент
u
ребро
и
x
вершина
если
u
ребру
инцидентна
x
вершина
если
b
j
i
j
i
ij
m
j
n
i
,
1
,
,
1
=
=
Каждый столбец матрицы инцидентности соответствует одному ребру
графа, поэтому в каждом столбце этой матрицы имеется ровно две единицы
(соответствующие двум вершинам – концам данного ребра).
78
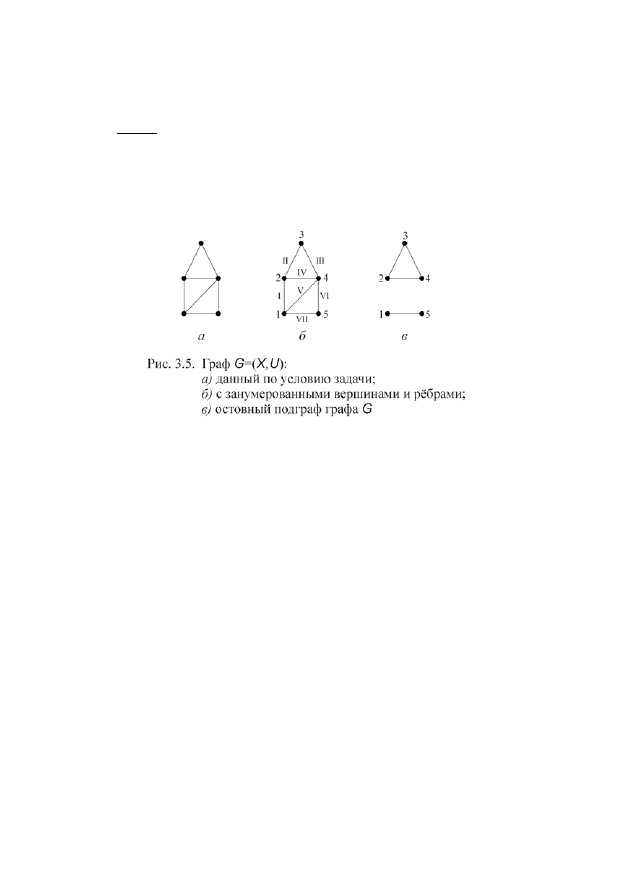
3.2.3. Решение задачи 6 контрольной работы №2
Задача. Дан неорграф
)
,
(
U
X
G
=
(рис. 3.5, а). Занумеруйте вершины
графа и определите степени всех его вершин. Нарисуйте какой-либо остовный
подграф графа
G
. Запишите матрицу смежности графа
G
. Занумеруйте ребра
графа и запишите его матрицу инцидентности.
Решение. Занумеруем вершины графа арабскими цифрами, а его ребра
римскими цифрами в произвольном порядке (рис. 3.5, б).
В остовный подграф
)
,
(
1
1
1
U
X
G
=
графа
)
,
(
U
X
G
=
включим все
вершины
X
X
=
1
и любое непустое подмножество ребер, например,
}
VII
IV,
III,
II,
{
1
=
U
рис.3.5, в. Перечислим степени вершин графа:
,
3
)
1
(
=
p
.
2
)
5
(
,
4
)
4
(
,
2
)
3
(
,
3
)
2
(
=
=
=
=
p
p
p
p
Матрица смежности
A
(ее размерность
5
5
×
) имеет вид:
⎥
⎥
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎡
=
0
1
0
0
1
1
0
1
1
1
0
1
0
1
0
0
1
1
0
1
1
1
0
1
0
5
4
3
2
1
5
4
3
2
1
A
.
Матрица инцидентности имеет размерность
7
5
×
и равна

79
⎥
⎥
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎡
=
1
1
0
0
0
0
0
0
1
1
1
1
0
0
0
0
0
0
1
1
0
0
0
0
1
0
1
1
1
0
1
0
0
0
1
5
4
3
2
1
VII
VI
V
IV
III
II
I
B
.
3.2.4. Контрольные вопросы и упражнения
1.
Перечислены степени всех вершин неорграфа:
2
,
2
,
1
,
3
,
2
. Сколько
ребер имеет этот граф? Нарисуйте такой граф.
2.
Какую степень имеет каждая вершина графа
5
K
?
3.
Нарисуйте двудольный граф
2
,
4
K
. Какую размерность имеют его
матрица смежности и матрица инцидентности?
4.
Сколько остовных подграфов можно построить для графа
3
K
?
5.
Докажите, что в неорграфе число вершин нечетной степени четно.
6.
Сколько различных подграфов имеет граф
3
K
?
7.
Граф, степени всех вершин которого одинаковы и равны числу
l
,
называется однородным степени
l
. Нарисуйте однородный степени 2
граф с пятью вершинами. Сколько существует однородных степени
2 графов с шестью вершинами?
3.3. Планарные графы
3.3.1. Изоморфизм графов
Пусть даны неорграфы
)
,
(
1
1
1
U
X
G
=
и
)
,
(
2
2
2
U
X
G
=
. Графы
1
G
и
2
G
называются изоморфными, если существует биекция
1
G
на
2
G
, сохра-
няющая отношение смежности. Это значит, что существует биекция (см. 1.4.1)
2
1
:
G
G
→
ϕ
такая, что вершины
1
,
X
y
x
∈
в графе
1
G
соединены ребром
1
U
u
∈
тогда и только тогда, когда в графе
2
G
их образы
2
)
(
)
(
),
(
X
y
x
x
∈
∈
ϕ
ϕ
ϕ
соединены ребром
2
)
(
U
u
∈
ϕ
. Из определения сле-
дует, что не могут быть изоморфными два графа, у которых не совпадает ко-
личество вершин или количество ребер.
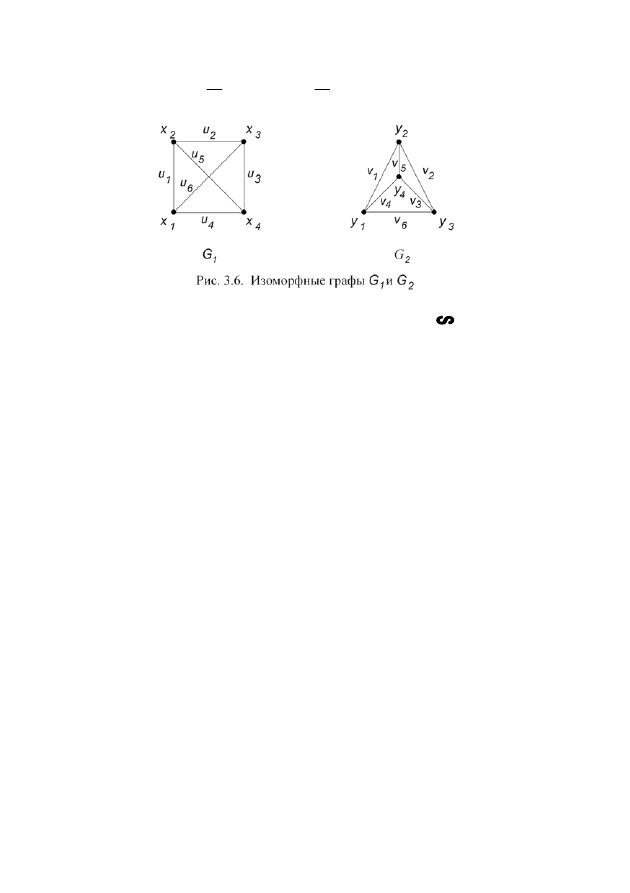
Пример. Графы
1
G
и
2
G
(рис. 3.6), изоморфны, т.к. имеют одинаковое
количество вершин и ребер (
6
,
4
2
1
2
1
=
=
=
=
U
U
X
X
), и можно биек-
тивно отобразить граф
1
G
на
2
G
, сохранив отношение смежности:
80
.
6
,
1
,
)
(
;
4
,
1
,
)
(
=
=
=
=
i
v
u
i
y
x
i
i
i
i
ϕ
ϕ
Для изоморфных графов используется обозначение
1
G
2
G
. Изоморф-
ные графы несут одинаковую информацию и отличаются только обозначения-
ми вершин и ребер. Матрицы смежности изоморфных графов могут быть по-
лучены друг из друга одновременными (одинаковыми) перестановками строк
и столбцов.
3.3.2. Планарность
Часто требуется изобразить граф так, чтобы его ребра не пересекались.
Например, при изготовлении микросхем печатным способом электрические
цепи наносятся на плоскую поверхность изоляционного материала. А так как
проводники не изолированы, то они не должны пересекаться. Аналогичной
является задача проектирования железнодорожных и других путей, где неже-
лательны переезды.
Назовем граф плоским, если его вершины являются точками плоскости,
а ребра – непрерывными плоскими линиями без самопересечений, причем
никакие два ребра не имеют общих точек, кроме инцидентной им вершины.
Любой граф, изоморфный плоскому графу, будем называть планарным. Так,
граф
2
G
(рис. 3.6) является плоским, а граф
1
G
– планарным (т.к. изоморфен
плоскому графу
2
G
). Существуют и непланарные графы. Один из них появля-
ется в задаче о “трех домах и трех колодцах”: имеются три дома и три колодца
(газ, вода и свет); требуется соединить каждый дом с каждым колодцем так,
чтобы линии соединения не пересекались. Моделью служит непланарный граф
3
,
3
K
. Также непланарным является граф
5
K
(рис. 3.7).