ВУЗ: Томский государственный университет систем управления и радиоэлектроники
Категория: Учебное пособие
Дисциплина: Дискретная математика
Добавлен: 28.11.2018
Просмотров: 10275
Скачиваний: 94

86
Так как число вершин графа
G
конечно, то в нем существует цикл
0
μ
(на
рис. 3.15, б выделен жирной линией). Если цикл
0
μ
содержит все ребра графа
G
, он является искомым эйлеровым. Если
0
μ
содержит не все ребра графа G,
то построим подграф
G
′
графа
G
, выбросив ребра, содержащиеся в
0
μ
(рис.
3.15, в). Подграф
G
′
не обязательно связный, но его можно разбить на компо-
ненты связности
p
G
G
G
,
,
,
2
1
…
(на рис. 3.15, в
2
=
p
). Каждая компонента
связности
,
i
G
p
i
,
1
=
, является связным графом, все вершины которого име-
ют четную степень, а число ребер
,
k
m
i
≤
p
i
,
1
=
. По индукционному пред-
положению для каждого графа
i
G
можно построить эйлеров цикл
i
μ
,
p
i
,
1
=
. Так как исходный граф
G
связен, то цикл
0
μ
имеет общие вершины
со всеми циклами
i
μ
,
p
i
,
1
=
. Тогда искомым эйлеровым циклом в
G
являет-
ся объединение циклов
p
μ
μ
μ
μ
,
,
,
,
2
1
0
…
. Индукционный переход доказан.
Следовательно, теорема справедлива для графов с любым числом ребер
3
≥
m
.
Теорема 2 (об эйлеровой цепи). В графе
G
существует эйлерова цепь то-
гда и только тогда, когда: 1) граф
G
связен; 2) граф
G
имеет ровно две верши-
ны нечетной степени.
Доказательство теоремы 2 аналогично доказательству теоремы 1.
3.4.4. Цикломатическое число
Пусть в графе
)
,
(
U
X
G
=
количество вершин
m
U
n
X
=
= ,
, количе-
ство компонент связности равно
k
. Цикломатическим числом графа G назы-
вается число
n
m
k
G
−
+
=
)
(
λ
.

87
Пример. Определим цикломатическое число для каждого из графов
i
G
,
4
,
1
=
i
(рис. 3.16).
Граф
1
G
является пустым графом и для него
4
,
0
,
4
=
=
=
k
m
n
, поэто-
му
0
4
0
4
)
(
1
=
−
+
=
G
λ
. Для графа
2
G
имеем
0
6
5
1
)
(
2
=
−
+
=
G
λ
. Для
3
G
-
;
1
4
4
1
)
(
3
=
−
+
=
G
λ
для
2
4
5
1
)
(
4
4
=
−
+
=
−
G
G
λ
.
Теорема. Цикломатическое число графа равно нулю тогда и только тогда,
когда в графе нет циклов.
Действительно, пусть
n
m
k
G
−
+
=
)
(
λ
. Рассмотрим остовный подграф
)
,
(
1
1
U
X
G
=
графа
)
,
(
U
X
G
=
, выбросив ребро
}
{
\
:
1
1
1
u
U
U
u
=
. Если в
графе
G
есть хотя бы один цикл, содержащий ребро
1
u
, то число компонент
связности не изменится; если же ни одного такого цикла нет, то число компо-
нент связности увеличится на единицу:
1
1
+
=
k
k
. Поэтому
+
=
1
1
)
(
k
G
λ
)
(
)
1
(
G
n
m
λ
≥
−
−
+
. Будем повторять эти рассуждения, выбрасывая по од-
ному ребру, пока не получим пустой подграф
n
m
O
G
=
. Для цепочки подгра-
фов
m
m
G
G
G
G
G
,
,
,
,
,
1
2
1
−
…
выполняются неравенства
)
(
)
(
)
(
)
(
)
(
1
2
1
m
m
G
G
G
G
G
λ
λ
λ
λ
λ
≥
≥
≥
≥
≥
−
…
,
причем
0
0
)
(
)
(
=
−
+
=
=
n
n
O
G
n
m
λ
λ
, и знак равенства сохранится на про-
тяжении всей цепочки тогда и только тогда, когда выбрасываются ребра, не
входящие ни в один цикл. Поэтому
0
)
(
)
(
=
=
n
O
G
λ
λ
тогда и только тогда,
когда в графе
G
нет циклов.
3.4.5. Решение задачи 8 контрольной работы №2
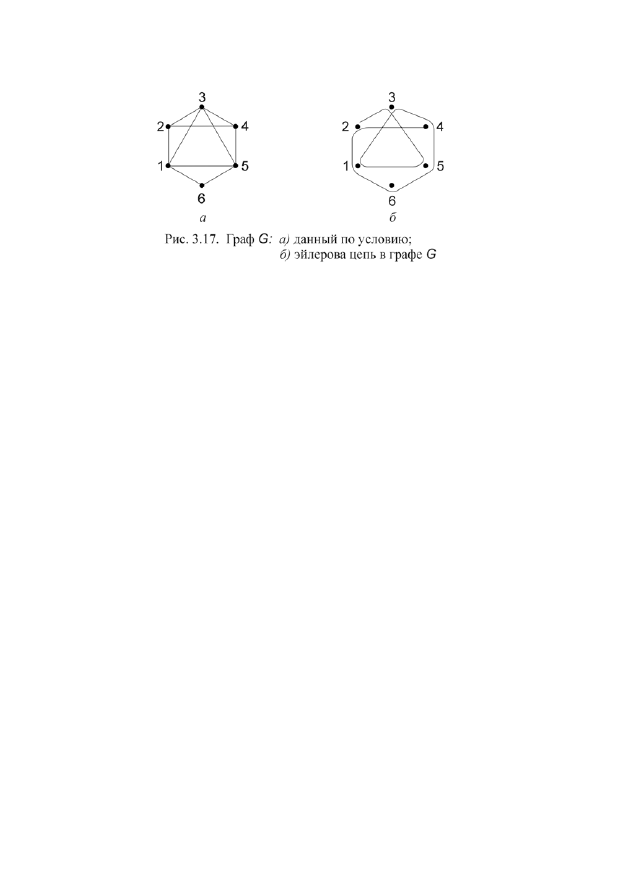
Задача. Для данного неорграфа
G
(рис. 3.17, а) определить цикломатиче-
ское число. Выяснить, можно ли нарисовать
G
, не отрывая руки от бумаги и не
проходя ни по одному ребру дважды.
Решение. Граф
G
является связным, поэтому число компонент связности
1
=
k
. Число вершин графа
6
=
n
, число ребер
10
=
m
. По определению цик-
ломатического числа
.
5
6
10
1
)
(
=
−
+
=
−
+
=
n
m
k
G
λ
88
Для ответа на второй вопрос определим степени всех вершин графа:
.
2
)
6
(
,
4
)
5
(
,
3
)
4
(
,
4
)
3
(
,
3
)
2
(
,
4
)
1
(
=
=
=
=
=
=
p
p
p
p
p
p
Граф связен, и ровно
две вершины (вторая и четвертая) имеют нечетную степень. По теореме об
эйлеровой цепи в графе существует эйлерова цепь, т.е. его можно нарисовать,
не отрывая руки от бумаги. Начальной и конечной вершинами этой цепи будут
вершины с нечетной степенью (один из вариантов приведен на рис. 3.17, б).
3.4.6. Контрольные вопросы и упражнения
1.
Нарисуйте граф
3
,
3
K
; постройте в нем цикл длины 4. Можно ли в
этом графе построить цикл нечетной длины?
2.
Нарисуйте граф, имеющий 6 вершин , 4 ребра, 3 компоненты связ-
ности. Чему равно его цикломатическое число?
3.
Связный граф задан матрицей смежности:
.
0
0
1
1
0
0
1
0
1
1
0
1
1
0
1
0
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
=
A
Чему равно его цикломатическое число?
4.
Сформулируйте теорему об эйлеровом цикле.
5.
Является ли эйлеровым граф
5
K
? А граф
6
K
?
6.
Сформулируйте теорему об эйлеровой цепи.
7.
Существует ли эйлерова цепь в графе
G
(рис. 3.12)?
8.
Может ли цикломатическое число графа принимать отрицательное
значение?
9.
Известно, что в графе
G
есть эйлеров цикл. Может ли его циклома-
тическое число равняться нулю?
89
3.5. Графы без циклов
3.5.1. Дерево и лес
Определение. Связный граф без циклов называется деревом. Несвязный
граф без циклов - лесом.
В качестве корня дерева может быть рассмотрена любая из его вершин.
Листом дерева будем называть вершину
x
степени единица:
1
)
(
=
x
p
. Ветвь
дерева – любая цепь, соединяющая корень с листом.
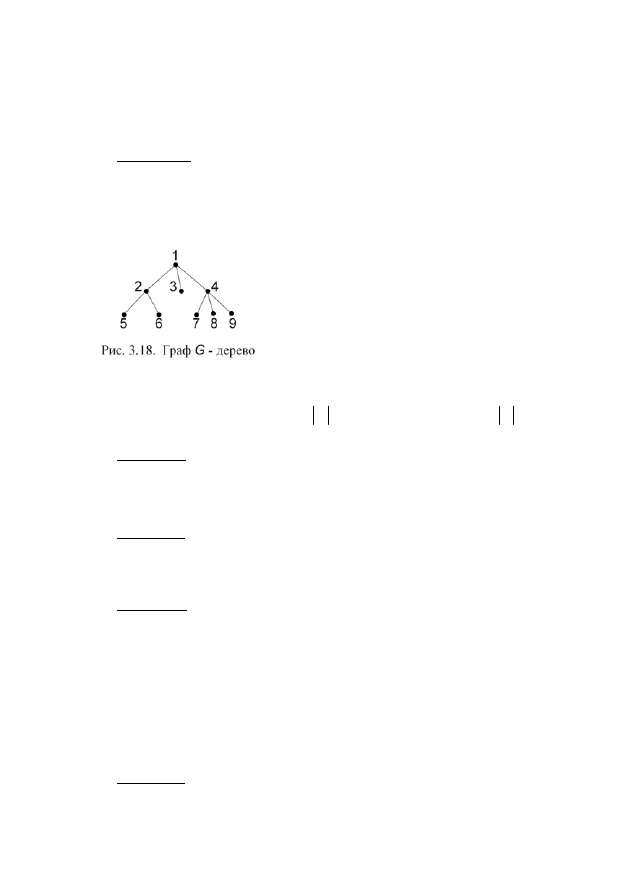
На рис. 3.18 в качестве корня рассматри-
вается вершина 1; листьями являются верши-
ны 3,5,6,7,8,9; ветви – цепи 1-2-5 или 1-4-8 и
т.п.
3.5.2. Свойства деревьев
Пусть в графе
X
n
U
X
G
=
=
)
,
(
- количество вершин,
U
m
=
- ко-
личество ребер,
k
– количество компонент связности.
Свойство 1. Граф
G
является деревом тогда и только тогда, когда его
цикломатическое число
0
)
(
=
G
λ
и число компонент связности
1
)
(
=
G
k
.
Это свойство является переформулировкой определения: дерево – связ-
ный граф, значит,
1
)
(
=
G
k
; дерево – граф без циклов, значит,
0
)
(
=
G
λ
.
Свойство 2. Если граф
G
– дерево, то количество его ребер на единицу
меньше количества вершин.
По свойству 1
0
)
(
=
−
+
=
n
m
k
G
λ
и
1
=
k
, отсюда
0
1
=
−
+
n
m
, т.е.
1
−
= n
m
.
Свойство 3. Любая пара вершин дерева может быть соединена един-
ственной простой цепью.
Предположим противное. Пусть найдутся вершины
X
y
x
∈
,
для кото-
рых нет такой цепи. Тогда граф
G
не является связным, что противоречит
условию (
G
– дерево).
Предположим теперь, что для некоторой пары вершин
X
y
x
∈
,
суще-
ствуют две простых цепи, соединяющих
x
и
y
. Тогда образуется цикл, но это
противоречит условию (
G
– дерево).
Следовательно, для любой пары вершин такая цепь существует и един-
ственна.
Свойство 4. Среди связных графов с заданным количеством вершин де-
рево является максимальным безцикловым графом.
90
Слово “максимальный” здесь означает, что добавление любого ребра к
дереву приводит к появлению цикла. Действительно, соединив любые две
несмежные вершины дерева ребром, получим цикл, т.к. по свойству 3 суще-
ствует цепь, соединяющая эти вершины.
Свойство 5. Дерево является минимальным связным графом.
Слово “минимальный” здесь означает, что удаление любого ребра при-
водит к нарушению связности. Цикломатическое число обладает свойством
0
)
(
≥
G
λ
, у дерева
0
)
(
=
−
+
=
n
m
k
G
λ
. Удалив ребро, получим подграф
G
G
⊆
1
, для которого
0
)
1
(
)
(
1
1
1
1
1
=
−
−
+
=
−
+
=
n
m
k
n
m
k
G
λ
, но по
свойству 2
1
−
= n
m
, отсюда
0
2
1
=
−
−
+
n
n
k
и
2
1
=
k
, т.е. граф
1
G
не-
связный.
3.5.3. Каркасы графа
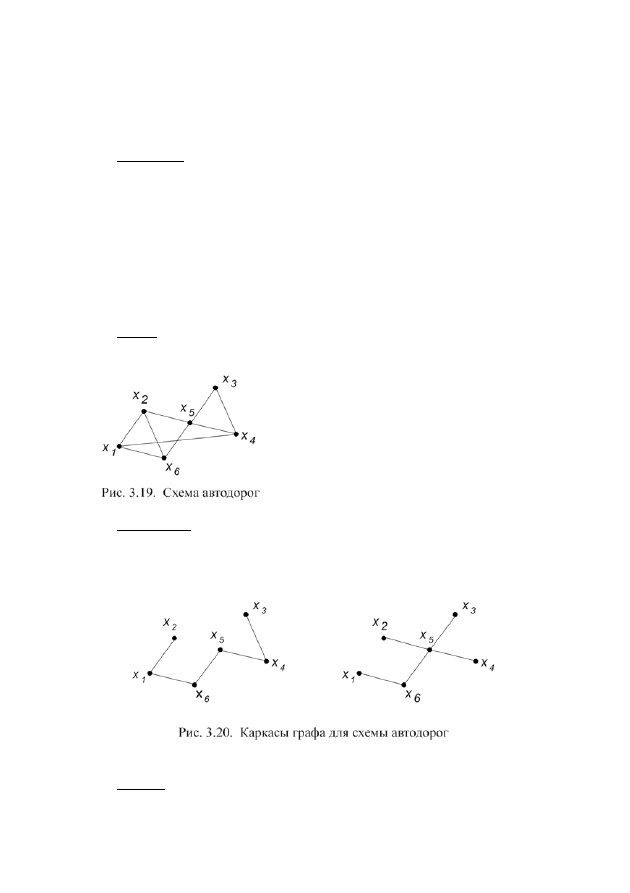
Задача. Шесть городов соединены сетью автодорог (рис. 3.19). Требуется
закрыть на ремонт наибольшее количество дорог так, чтобы связь между горо-
дами сохранилась.
В этой задаче имеем связный граф
)
,
(
U
X
G
=
и требуется построить его остов-
ный
связный
подграф
)
,
(
1
1
U
X
G
=
с
наименьшим количеством ребер. По свойству
5 (см. 3.5.2)
1
G
– дерево.
Определение. Каркасом графа
G
называется остовный подграф графа
G
с
тем же числом связности, но без циклов.
Очевидно, что каркас связного графа – дерево, несвязного – лес. Каркас
может быть построен не единственным образом. На рис. 3.20 приведены два
различных каркаса для схемы автодорог (рис. 3.19).
Сколько ребер нужно удалить, чтобы построить каркас графа?
Теорема. Чтобы построить каркас графа, нужно удалить
)
(G
λ
ребер.