ВУЗ: Томский государственный университет систем управления и радиоэлектроники
Категория: Учебное пособие
Дисциплина: Дискретная математика
Добавлен: 28.11.2018
Просмотров: 10274
Скачиваний: 94
91
Докажем
теорему
для
связного
графа
)
,
(
U
X
G
=
,
1
)
(
,
,
=
=
=
G
k
m
U
n
X
. Пусть
)
,
(
1
1
U
X
G
=
– каркас графа G. Найдем
разность
)
(
)
(
1
G
m
G
m
−
. Так как
1
G
– дерево, то
1
1
)
(
)
(
1
1
−
=
−
=
n
G
n
G
m
.
Значит, при построении каркаса удалено
=
+
−
=
−
1
)
(
)
(
1
n
m
G
m
G
m
)
(
1
G
n
m
λ
=
−
+
=
ребер.
Для несвязного графа теорема доказывается аналогично (строится каркас
для каждой компоненты связности).
Для графа на рис. 3.19
4
6
9
1
)
(
=
−
+
=
G
λ
– нужно удалить 4 ребра. По-
этому его каркасы (рис. 3.20) содержат
5
4
9
4
=
−
=
−
n
ребер.
Какие ребра нужно удалить для построения каркаса? Рассмотрим два ме-
тода построения каркаса графа.
3.5.4. Обход графа “в ширину”
Идея метода заключается в следующем. Начинаем обход графа из про-
извольной вершины, которой присваиваем метку “1”. Вершинам, смежным с
помеченной, присвоим метки
1
,
,
3
,
2
r
…
. Далее нумеруем непомеченные вер-
шины, смежные с 2; затем непомеченные вершины, смежные с 3 и т.д., пока не
занумеруем все вершины, смежные с уже помеченными. Если в графе есть
непомеченные вершины, то процесс повторяется, пока всем вершинам не бу-
дут присвоены метки. Покажем применение этого метода для построения кар-
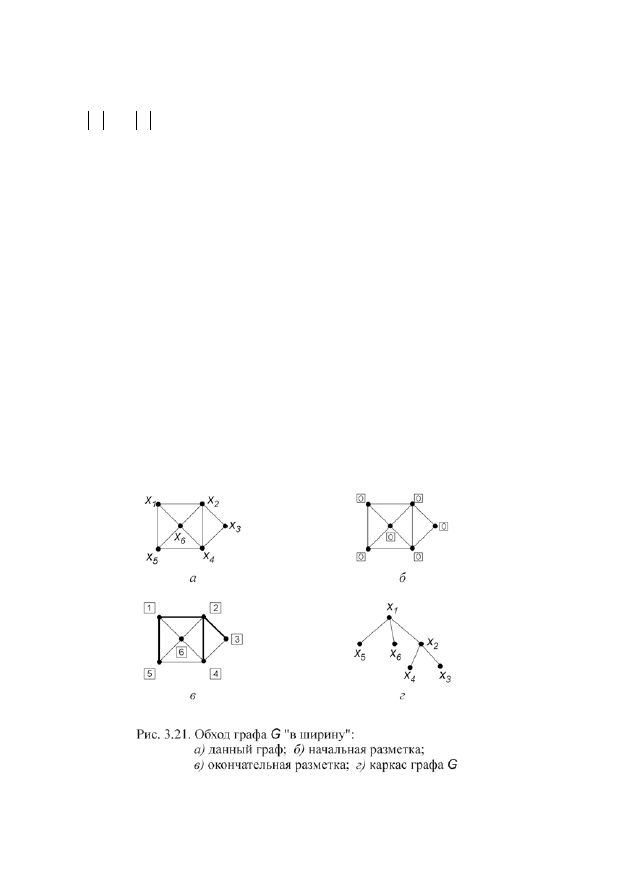
каса графа. Дан граф
G
(рис. 3.21, а).
92
Присвоим всем его вершинам метки “0”(рис. 3.21, б). Начинаем разметку
с вершины
1
x
: она получает метку “1”. Вершине
1
x
смежны вершины
5
6
2
,
,
x
x
x
, имеющие метку “0”. Присваиваем им новые метки “2”, “3”, “4” и
включаем в каркас соответствующие ребра (выделены жирной линией на рис.
3.21, в). Вершина
2
x
имеет метку “2”, ей смежны вершины
6
4
3
,
,
x
x
x
. Но
вершина
6
x
уже имеет метку, большую нуля, поэтому новые метки “5” и “6”
получают вершины
3
x
и
4
x
. Включаем в каркас ребра
}
,
{
3
2
x
x
и
}
,
{
4
2
x
x
.
Рассмотрим вершину с меткой “3”. Все вершины, смежные ей, уже имеют мет-
ки, большие нуля, поэтому новые ребра к каркасу не добавляем. То же можно
сказать и о вершинах с метками “4”, “5”, “6”. Каркас графа
G
приведен на рис.
3.21, г.
Обход графа в “ширину” приводит к “разветвленным” деревьям с корот-
кими ветвями.
Если граф несвязный, то разметка проводится для каждой его компонен-
ты связности.
3.5.5. Обход графа “в глубину”
Этот метод приводит к деревьям малоразветвленным, с длинными ветвя-
ми.
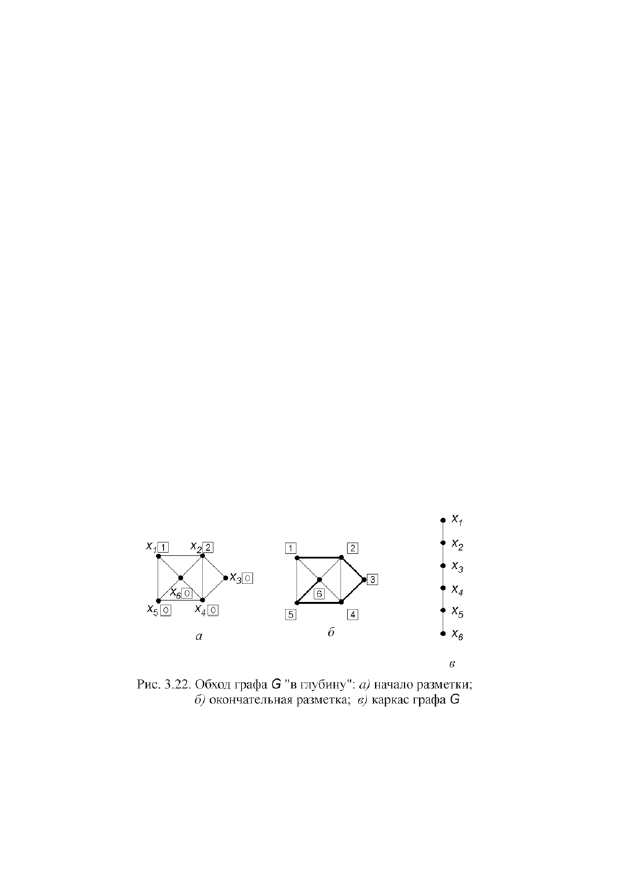
Продемонстрируем обход “в глубину” для графа
G
(рис. 3.21, а). Всем
вершинам присвоим метку “0” (рис. 3.21, б). Начинаем разметку из вершины
1
x
с меткой “1”; вершине
2
x
присваиваем метку “2”, ребро
}
,
{
2
1
x
x
включа-
ем в каркас (рис. 3.22, а).
Далее ищем вершину с нулевой меткой, смежную вершине “2” – присва-
иваем ей метку “3”, включаем соединяющее их ребро в каркас и так далее, до
тех пор, пока все вершины не получат отличные от нуля метки. Каркас графа
G
построен (рис. 3.22, в).
93
3.5.6. Решение задачи 9 контрольной работы №2
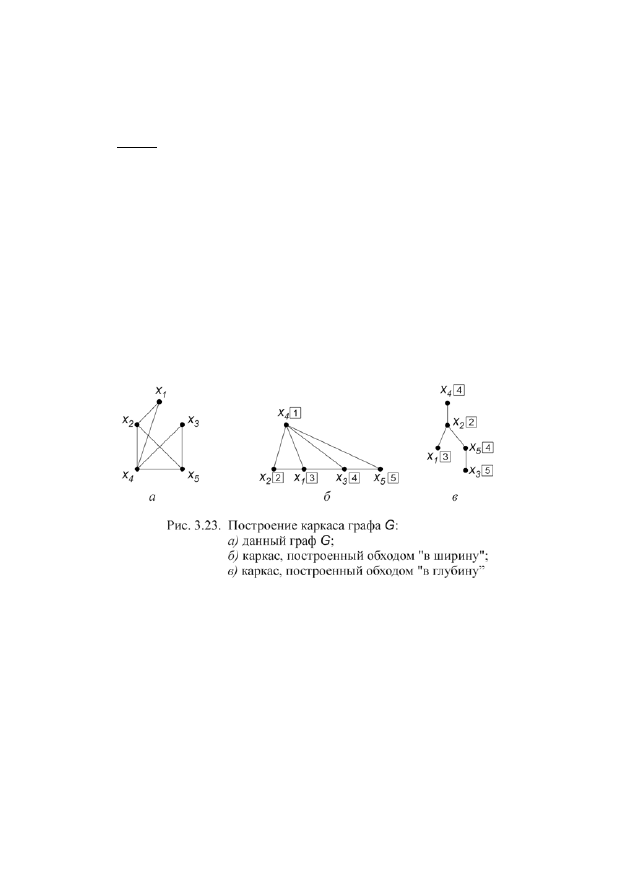
Задача. Для данного графа
G
(рис. 3.23, а) выяснить, сколько ребер нуж-
но удалить, чтобы построить его каркас. Построить каркас графа двумя спосо-
бами (обход “в глубину”, обход “в ширину”), начиная обход из вершины с
максимальной степенью.
Решение. Согласно теореме из 3.5.3 количество удаляемых ребер при по-
строении каркаса равно цикломатическому числу графа. Для графа
G
,
1
,
6
,
5
=
=
=
k
m
n
поэтому цикломатическое число
=
−
+
=
n
m
k
G)
(
λ
3
5
7
1
=
−
+
=
, т.е. для построения каркаса нужно удалить 3 ребра графа.
Максимальную степень имеет вершина
4
x
:
4
)
(
4
=
x
p
. Будем строить каркас
с помощью обхода “в ширину” из вершины
4
x
(метка “1”). Метки “2”, “3”,
“4”, “5” получат вершины
5
3
1
2
,
,
,
x
x
x
x
. Включаем в каркас ребра, соединяю-
щие эти вершины с вершиной
4
x
, и построение каркаса закончено (рис. 3.23,
б).
Присвоим вновь метку “1” вершине
4
x
. Будем строить каркас, обходя
граф “в глубину”. Метку “2” получит вершина
2
x
(включаем в каркас ребро
}
,
{
2
4
x
x
). Метку “3” – вершина
1
x
(включаем ребро
}
,
{
1
2
x
x
). Все вершины,
смежные
1
x
, уже имеют ненулевые метки, поэтому возвращаемся из вершины
1
x
в вершину
2
x
. Вершина
5
x
смежна вершине
2
x
и не имеет метки. При-
сваиваем ей метку “4” и включаем в каркас ребро
}
,
{
5
2
x
x
. Следующую метку
“5” получает вершина
3
x
, в каркас включаем ребро
}
,
{
3
5
x
x
. Все вершины
имеют ненулевые метки, в каркас включено
4
3
7
)
(
=
−
=
− G
m
λ
ребра, его
построение закончено (рис. 3.23, в).

94
3.5.7. Контрольные вопросы и упражнения
1.
Какой граф называется деревом?
2.
Сколько ребер может быть у дерева с шестью вершинами?
3.
Что произойдет с цикломатическим числом дерева, если удалить од-
но из его ребер?
4.
Какое наименьшее количество ребер может иметь связный граф с 16
вершинами?
5.
Докажите, что всякое дерево, имеющее хотя бы одно ребро, имеет
хотя бы один лист.
6.
Что такое каркас графа?
7.
Всегда ли каркас графа является деревом?
8.
Сколько ребер нужно удалить, чтобы построить каркас графа
4
K
?

95
ПРИЛОЖЕНИЕ 1
Контрольная работа № 1