ВУЗ: Томский государственный университет систем управления и радиоэлектроники
Категория: Учебное пособие
Дисциплина: Дискретная математика
Добавлен: 28.11.2018
Просмотров: 10270
Скачиваний: 94
96
Вариант 1
1. Решить задачу, используя диаграмму Эйлера-Венна.
Четырнадцать спортсменов участвовали в кроссе, 16 – в соревнованиях
по плаванию, 10 – в велосипедных гонках. Восемь участников участвовали в
кроссе и заплыве, 4 – в кроссе и велосипедных гонках, 9 – в плавании и вело-
сипедных гонках. Во всех трех соревнованиях участвовали три человека.
Сколько всего было спортсменов?
2. Задано универсальное множество
}
8
,
7
,
6
,
5
,
4
,
3
,
2
,
1
{
=
U
и множества
}
8
,
7
,
4
,
3
{
},
8
,
7
,
4
,
3
{
},
7
,
6
,
3
,
1
{
=
=
=
Z
Y
X
. Построить булеан множества
X
и любое разбиение множества
Z
. Выполнить действия
.
)
\
(
Z
Y
X
∩
3. Доказать, используя законы и тождества алгебры множеств (перечис-
лить используемые законы):
.
)
(
)
(
)
(
B
C
A
C
B
B
A
∩
∩
=
∩
∪
∩
4. Пусть
}
4
,
3
,
2
,
1
{
=
X
. Бинарное отношение
X
X
R
×
⊆
задано харак-
теристическим свойством:
}
,
четное,
)
,
{(
X
b
a
b
a
b
a
R
∈
−
+
=
.
Представить отношение различными способами. Выяснить, какими свой-
ствами оно обладает.
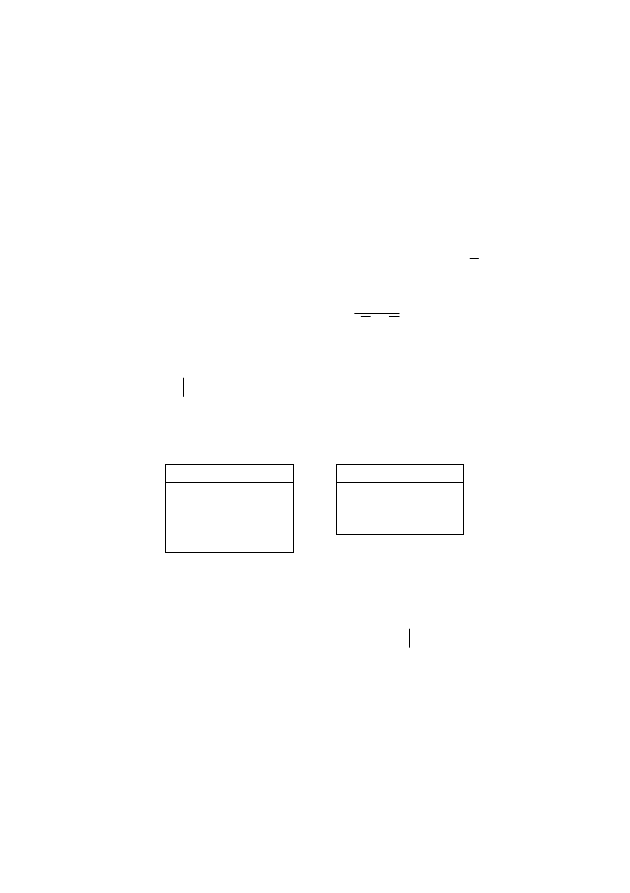
5. Заданы отношения:
R: S:
A
1
A
2
A
3
B
1
B
2
B
3
a
b
C
a
d
b
a c d a c d
b d a b d a
d
a
b
Записать обозначения операций и выполнить их:
а) селекция отношения
R
по условию “
b
A
>
2
”;
б) проекция на список (3,1) объединения отношений
R
и
S
.
6. Даны множества
}
1
,
0
,
1
{
−
=
A
и
∈
−
=
n
n
B
2
3
{
N
}. Какова мощ-
ность множеств
B
A
B
A
B
A
×
∪
∩
,
,
?
7. Шесть старушек вышли во двор поболтать. На скамейке помещаются
только четыре из них. Сколькими способами их можно рассадить на скамейке?
8. На веревке сушатся четыре белых полотенца и три желтых. Сколькими
способами их можно развесить, если полотенца одного цвета не отличаются
друг от друга?
97
Вариант 2
1. Решить задачу, используя диаграмму Эйлера-Венна.
В туристском клубе несколько раз за лето организуются походы, причем
все члены клуба хотя бы раз в них участвуют. Сорок человек побывали в пе-
ших походах, 28 – в конных, 25 – в лодочных. И в пеших, и в конных походах
побывало 20 человек, в пеших и лодочных – 15, в конных и лодочных – 8, во
всех видах походов побывало 6 человек. Сколько туристов в клубе?
2. Задано универсальное множество
}
8
,
7
,
6
,
5
,
4
,
3
,
2
,
1
{
=
U
и множества
}
8
,
7
,
2
,
1
{
},
6
,
4
,
2
,
1
{
},
8
,
7
,
6
,
5
,
3
{
=
=
=
Z
Y
X
. Построить булеан множества
Y
и любое разбиение множества
X
. Выполнить действия
.
)
(
X
Y
Z
∪
∩
3. Упростить, используя законы и тождества алгебры множеств (пере-
числить используемые законы):
).
(
)
(
)
(
B
A
B
A
B
A
∩
∪
∩
∪
∪
4. Пусть
}
5
,
4
,
3
,
2
,
1
{
=
X
. Отношение
X
X
R
×
⊆
задано характери-
стическим свойством:
}
,
,
5
)
,
{(
X
b
a
b
a
b
a
R
∈
<
+
=
.
Задать отношение другими возможными способами. Выяснить, какими
свойствами оно обладает.
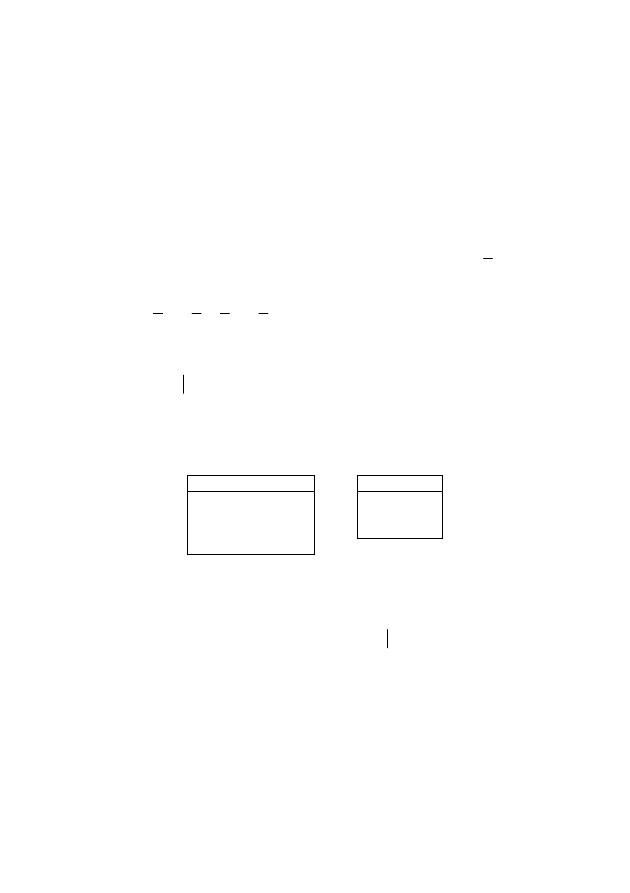
5. Заданы отношения:
R: S:
A
1
A
2
A
3
B
1
B
2
a
b
c
a
d
a c d a c
b d a с
d
d a b
Записать обозначения операций реляционной алгебры и выполнить их:
а) проекция отношения
R
на список (1,3);
б) соединение отношений
R
и
S
по условию “
1
2
B
A
=
”.
6. Даны множества
}
3
,
2
,
1
{
=
A
и
∈
−
=
n
n
B
1
3
{
N
}. Какова мощность
множеств
B
A
B
A
B
A
×
∪
∩
,
,
?
7. На подоконнике стоят четыре горшка с цветами. Сколькими способами
их можно расставить на подоконнике?
8. Шесть мячей раскладывают по двум коробкам. Сколькими способами
это можно сделать? (Считается, что вместимость коробки достаточна для всех
мячей).

98
Вариант 3
1. Решить задачу, используя диаграмму Эйлера-Венна.
В отделе НИИ работают несколько человек, причем каждый из них знает
хотя бы один иностранный язык. Английский язык знают шесть человек,
немецкий – шесть человек, французский – семь. Четыре человека знают ан-
глийский и немецкий языки, три человека – немецкий и французский, два –
французский и английский, один знает все три языка. Сколько человек работа-
ет в отделе?
2. Задано универсальное множество
}
8
,
7
,
6
,
5
,
4
,
3
,
2
,
1
{
=
U
и множества
}
7
,
5
,
2
,
1
{
},
8
,
6
,
5
,
3
,
1
{
},
8
,
7
,
6
,
5
{
=
=
=
Z
Y
X
. Найти булеан множества
X
и
какое-либо разбиение множества
Y
. Выполнить действия
).
\
(
Z
Y
X
∩
3. Упростить, используя законы и тождества алгебры множеств (пере-
числить используемые законы):
).
(
)
(
)
(
B
A
B
A
B
A
∪
∪
∩
∪
∩
4. Пусть
}
3
,
2
,
1
,
0
,
1
,
2
{
−
−
=
X
. Бинарное отношение
X
X
R
×
⊆
задано
характеристическим свойством:
}
,
,
3
)
,
{(
X
b
a
b
a
b
a
R
∈
=
+
=
.
Представить отношение
R
другими возможными способами. Выяснить,
какими свойствами оно обладает.
5. Заданы отношения:
R: S:
A
1
A
2
A
3
B
1
B
2
a
b
D
b
c
b c D a c
b a D a
d
a b C
Записать обозначения операций реляционной алгебры и выполнить их:
а) проекция отношения
R
на список (1,3);
б) соединение отношений
R
и
S
по условию “
1
1
B
A
>
”.
6. Даны множества
}
3
,
2
,
1
,
0
{
=
A
и
∈
−
=
n
n
B
2
4
{
N
}. Какова мощ-
ность множеств
B
A
B
A
B
A
×
∪
∩
,
,
?
7. Пятнадцать студентов пришли на занятия, но в аудитории оказалось
только
13
стульев. Сколькими способами они могут выбрать двоих, чтобы
отправить их на поиски стульев?
8. Сколькими способами можно расставить семь катеров у двух прича-
лов, если у каждого причала могут поместиться все семь? Способы различают-
ся лишь количеством катеров у каждого причала.

99
Вариант 4
1. Решить задачу, используя диаграмму Эйлера - Венна.
Из 80 студентов занимаются баскетболом 30 человек, легкой атлетикой
25 человек, шахматами - 40 человек. Баскетболом и легкой атлетикой занима-
ется 8 человек, шахматами и легкой атлетикой – 10 человек, шахматами и бас-
кетболом – 5 человек. Тремя видами спорта занимаются три человека. Сколько
человек занимаются спортом?
2. Задано универсальное множество
}
8
,
7
,
6
,
5
,
4
,
3
,
2
,
1
{
=
U
и множества
}
8
,
5
,
3
,
1
{
},
8
,
7
,
6
,
3
,
2
{
},
8
,
7
,
6
,
5
,
1
{
=
=
=
Z
Y
X
. Найти булеан множества
Z
и
какое-либо разбиение множества
X
. Выполнить действия
)
\
(
Z
X
Y
∩
.
3. Доказать, используя законы и тождества алгебры множеств (перечис-
лить используемые законы):
.
)
(
B
A
B
B
A
A
∪
=
∪
∩
∩
4. Отношение
R
на множестве
X
задано перечислением своих элементов:
)}
3
,
3
(
),
1
,
3
(
),
1
,
2
(
),
2
,
2
(
),
1
,
1
(
),
2
,
1
{(
=
R
. Нарисуйте график, схему и граф от-
ношения. Запишите его матрицу. Какими свойствами обладает отношение?
Является ли оно отношением эквивалентности? Объясните ответ.
5. Заданы отношения:
R: S:
A
1
A
2
A
3
B
1
B
2
с
e f f d
a b d e c
d e f
c d c
Записать обозначения операций реляционной алгебры и выполнить их:
а) проекция отношения
R
на список (2,3);
б) соединение отношений
R
и
S
по условию “
1
3
B
A
=
”.
6. Даны множества
}
3
,
2
,
1
{
=
A
и
∈
−
=
n
n
B
3
4
{
N
}. Какова мощность
множеств
B
A
B
A
B
A
×
∪
∩
,
,
?
7. Семеро студентов пошли вместо лекции в кино. Но оказалось, что в
кассе осталось только три билета. Сколькими способами они могут выбрать
этих троих?
8. Сколькими способами можно рассадить шесть кустов пионов на трех
клумбах, если на каждой клумбе могут поместиться все шесть?

100
Вариант 5
1. Решить задачу, пользуясь диаграммой Эйлера-Венна.
Десять читателей взяли в библиотеке фантастику, 11 – детективы, 8 –
приключения. Фантастику и приключения взяли 4 человека, фантастику и де-
тективы – 6, приключения и детективы – 3, двое взяли три вида книг. Сколько
читателей побывало в библиотеке?
2. Задано универсальное множество
}
8
,
7
,
6
,
5
,
4
,
3
,
2
,
1
{
=
U
и множества
}
8
,
6
,
5
,
1
{
},
6
,
4
,
3
,
2
,
1
{
},
8
,
7
,
5
,
4
,
2
{
=
=
=
Z
Y
X
. Найти булеан множества
Z
и какое-либо разбиение множества
Y
. Выполнить действия
)
(
\
Y
Z
X
∩
.
3. Упростить, используя законы и тождества алгебры множеств (пере-
числить используемые законы):
.
)
(
)
(
B
C
B
B
B
A
A
∪
∪
∩
∪
∪
∩
4. Пусть
}
4
,
3
,
2
,
1
,
0
{
=
X
. Бинарное отношение
X
X
R
×
⊆
задано ха-
рактеристическим свойством:
}
,
,
3
на
делится
)
,
{(
X
b
a
b
a
b
a
R
∈
+
=
.
Представить отношение
R
другими возможными способами. Какими
свойствами оно обладает?
5. Заданы отношения:
R: S:
A
1
A
2
A
3
B
1
B
2
B
3
a
b
c
a
c
b
b a c a d e
a c b a d b
a
d
b
Записать обозначения операций реляционной алгебры и выполнить их:
а) селекция отношения
R
по условию “
3
2
A
A
>
”;
б) проекция на список (3,1) объединения отношений
R
и S.
6. Даны множества
}
2
,
1
,
0
{
=
A
и
∈
−
=
n
n
B
4
5
{
N
}. Какова мощность
множеств
B
A
B
A
B
A
×
∪
∩
,
,
?
7. Семеро рыбаков отправились на остров на двух лодках. Ночью одна из
лодок уплыла. Сколькими способами они могут отправить троих в погоню за
уплывшей лодкой?
8. Сколькими различными способами можно разложить восемь монет
различного достоинства в два кармана?