ВУЗ: Томский государственный университет систем управления и радиоэлектроники
Категория: Учебное пособие
Дисциплина: Дискретная математика
Добавлен: 28.11.2018
Просмотров: 10280
Скачиваний: 94

36
1.4.9. Несчетные множества
Рассмотрим множество
⊂
=
]
1
;
0
[
X
R
. Сравним его с множеством
N
.
Очевидно, что
≥
]
1
;
0
[
⏐
N
⏐. Действительно, отрезок [0;1] содержит счетное
подмножество
,...}
,...,
,
,
,
1
{
1
4
1
3
1
2
1
n
, значит, является не менее, чем счетным.
Покажем, что [0;1] и
N
не являются равномощными множествами, т.е. что
0
]
1
;
0
[
ℵ
≠
.
Теорема. Множество точек отрезка [0;1] не является счетным.
Проведем доказательство методом “от противного”. Предположим, что
множество [0;1] счетно, т.е. существует биекция
N
на [0;1], и каждому элемен-
ту отрезка можно присвоить номер:
∈
∈
=
i
a
a
i
i
],
1
;
0
[
{
]
1
;
0
[
N
}. Каждый
элемент отрезка [0;1] представляется в виде бесконечной десятичной дроби
…
3
2
1
,
0
i
i
i
i
a
α
α
α
=
, где
j
i
α
–
j
-я десятичная цифра
i
-го элемента. Запишем
все элементы
∈
i
a
i
,
N
, в порядке возрастания номеров. Покажем, что найдет-
ся элемент
b
, принадлежащий отрезку [0;1], но не совпадающий ни с одним из
занумерованных элементов
∈
i
a
i
,
N
. Метод построения такого элемента
называется диагональной процедурой Кантора и заключается в следующем.
Будем строить элемент
b
в виде бесконечной десятичной дроби
…
3
2
1
,
0
β
β
β
=
b
, где
i
β
–
i
-я десятичная цифра. В качестве
1
β
возьмем лю-
бую цифру, не совпадающую с
11
α
,
2
β
– любую цифру, не совпадающую с
22
α
, ... ,
nn
n
α
β
≠
при любых
∈
n
N
(рис. 1.24). Построенный таким образом
элемент
b
принадлежит отрезку [0;1], но отличается от каждого из занумеро-
ванных элементов
i
α
хотя бы одной цифрой. Следовательно, предположение
о том, что существует биекция
:
f
N
→ [0;1] ошибочно, и множество [0;1] не
является счетным.
Итак, мы показали, что
⏐[0;1]⏐>⏐
N
⏐, т.е. класс эквивалентности, кото-
рому принадлежит отрезок [0;1], расположен правее класса
ℵ
0
счетных мно-
37
жеств в ряду мощностей (рис. 1.23). Обозначим этот класс
ℵ
(без индекса).
Множества, принадлежащие этому классу, называются несчетными или мно-
жествами мощности континуум (континуум – непрерывный). Этому классу
принадлежат и интервал (0;1), и множество
R
действительных чисел, и мно-
жество точек круга на плоскости.
Пример. Множество
R
имеет мощность континуума, т.к. равномощно
отрезку [0;1]. Действительно, по теореме Кантора-Бернштейна (см. 1.4.4)
⏐[0;1]⏐= ⏐(0;1)⏐. Биекцию интервала (0;1) на множество
R
можно задать с
помощью сложной функции
))
(
(
x
g
f
y
=
, где
)
(x
g
z
=
имеет вид
2
π
π
−
=
x
z
и отображает интервал (0;1) на интервал
)
;
(
2
2
π
π
−
, а
)
(z
f
y
=
отображает интервал
)
;
(
2
2
π
π
−
на
R
по закону
z
tg
y
=
.
1.4.10. Выводы
Итак, используя понятие “мощность”, мы сравниваем между собой не
только конечные, но и бесконечные множества. Мощность – это то общее, что
есть у всех равномощных множеств, а общим у них является класс эквива-
лентности. Мы говорим, что множество имеет мощность
ℵ
0
, и это означает,
что оно принадлежит тому же классу эквивалентности, что и множество нату-
ральных чисел; мы говорим, что множество имеет мощность континуума, и
это означает, что оно принадлежит тому же классу, что и отрезок [0;1] (табл.
1.5).
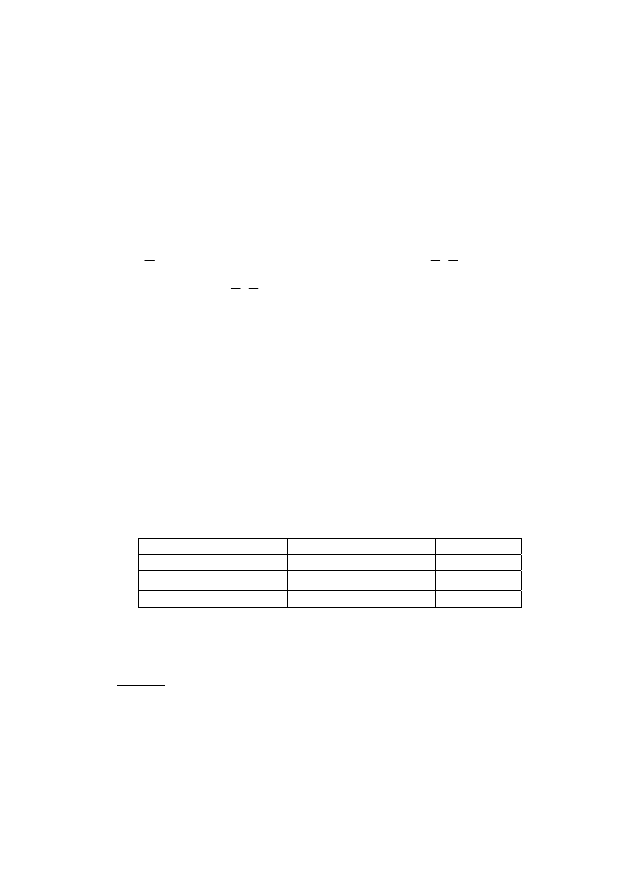
Таблица 1.5
Мощность множества
Множество
Эталон
Мощность
Конечное
{1, 2, … ,n}
n
Счетное
N
ℵ
0
Несчетное [0;1]
ℵ
Мы показали, что несчетные множества имеют мощность большую, чем
счетные. А существуют ли множества наибольшей мощности ? На этот вопрос
отвечает теорема, которую мы приведем без доказательства.
Теорема. Пусть
X
– бесконечное множество. Мощность булеана множе-
ства X больше мощности множества
X
.
На основании этой теоремы мы можем утверждать, что не существует
множества наибольшей мощности: для каждого множества
X
мы можем по-
строить его булеан, т.е. множество большей мощности. Это означает, что ряд
мощностей (рис. 1.23) неограничен.

38
1.4.11. Решение задачи 6 контрольной работы 1
Задача. Даны множества
}
0
,
1
,
2
{
−
−
=
A
и
∈
−
=
n
n
B
1
4
{
N
}. Какова
мощность множеств
B
A
B
A
B
A
×
∪
∩
,
,
?
Решение. Множество
A
конечно и задано перечислением своих элемен-
тов, множество
B
задано характеристическим свойством. Запишем несколько
первых элементов множества
}
,
15
,
11
,
7
,
3
{
…
=
B
. Видим, что
=
∩
B
A
∅
и
0
=
∩
B
A
, т.е. множество
B
A
∩
конечно.
Покажем, что множество
}
,
15
,
11
,
7
,
3
,
0
,
1
,
2
{
…
−
−
=
∪
B
A
счетно. Зану-
меруем его элементы:
⎪
⎩
⎪
⎨
⎧
≥
−
∈
=
=
−
=
.
3
,
13
4
.
,
2
,
0
,
1
,
2
n
n
N
n
n
n
z
n
Задана биекция множества
N
на множество
B
A
∪
, следовательно,
B
A
∪
счетно и
0
ℵ
=
∪ B
A
.
По определению декартова произведения
}
,
)
,
{(
B
b
A
a
b
a
B
A
∈
∈
=
×
.
Запишем элементы этого множества в виде матрицы (рис. 1.25) и занумеруем
его по столбцам.
Замечаем, что если номер
n
делится на 3 без остатка, то первый элемент
пары равен 0; если номер
n
делится на 3 с остатком 1, то первый элемент пары
равен –2; если номер
n
делится на 3 с остатком 2, то первый элемент пары
равен -1. Поэтому способ нумерации может быть задан следующим образом:
⎪
⎩
⎪
⎨
⎧
−
=
−
−
∈
−
=
−
−
=
−
=
.
1
3
),
1
4
,
1
(
,
,
2
3
),
1
4
,
2
(
,
3
),
1
4
,
0
(
k
n
если
k
N
k
k
n
если
k
k
n
если
k
z
n
и множество
B
A
×
счетно, т.е. имеет мощность
ℵ
0
.

39
1.4.12. Контрольные вопросы и упражнения
1.
Является ли биекцией отображение
2
)
(
x
x
f
=
, заданное на отрезке
[-1;1]? А заданное на [0;1]?
2.
Являются ли равномощными множества
]
1
;
0
[
=
X
и
]
0
;
2
[
−
=
Y
?
3.
Являются ли равномощными множество
}
2
,
1
{
=
X
и множество
корней квадратного уравнения
0
4
2
=
+
+ x
x
?
4.
Сформулируйте теорему Кантора-Бернштейна.
5.
Покажите, пользуясь теоремой Кантора-Бернштейна, что множества
]
1
;
0
[
=
X
и
]
5
;
4
[
]
3
;
0
[
∪
=
Y
равномощны.
6.
Даны множества
}
7
,
5
,
2
{
=
X
и
}
8
,
6
,
3
{
=
Y
. Чему равно
Y
X
∪
?
7.
Впишите ответ:
Если
}
7
,
5
,
2
{
=
X
,
}
8
,
5
,
3
{
=
Y
, то
=
∪Y
X
________ .
8.
Пусть
}
4
,
2
{
=
X
. Тогда
⏐
B
(
X
)
⏐=______,
B
(
X
)={______________}.
9.
Сколько подмножеств имеет множество
}
7
,
5
,
3
,
1
{
=
X
?
10.
Какое множество называется счетным?
11.
Покажите, что множество целых чисел
Z
счетно.
12.
Мощность счетного множества обозначается _____ .
13.
Сформулируйте свойства счетных множеств.
14.
Множество
X
– все натуральные числа, делящиеся на 3, множество
Y
– натуральные числа, делящиеся на 4. Какова мощность множе-
ства
Y
X
∪
?
15.
Какова мощность множества
N
]
5
;
1
[
∩
?
16.
Мощность несчетного множества обозначается буквой ______ .
17.
Какова мощность множества
N
]
1
;
0
[
∪
?
18.
Существует ли множество наибольшей мощности?
40
1.5. Комбинаторика
1.5.1. Задачи комбинаторики
Комбинаторика решает для конечных множеств задачи следующего типа:
а) выяснить, сколько существует элементов, обладающих заданным
свойством;
б) составить алгоритм, перечисляющий все элементы с заданным свой-
ством;
в) отобрать наилучший по некоторому признаку среди перечисленных
элементов.
Мы будем заниматься только задачами первого типа. При этом будет ид-
ти речь об отборе
r
элементов с заданным свойством из конечного множества
X
, состоящего из
n
элементов. Результат такого отбора будем называть выбор-
кой. Нас будет интересовать вопрос о количестве выборок заданного типа.
1.5.2. Типы выборок
Выборки делятся на типы по двум признакам: а) важен ли порядок отбо-
ра элементов; б) есть ли среди отобранных элементов одинаковые. Будем обо-
значать
n
– количество элементов в исходном множестве
X
,
r
– количество
элементов в выборке.
Упорядоченный набор элементов, среди которых нет повторяющихся,
называется размещением из
n
элементов по
r
. Количество размещений обо-
значается
A
r
n
(табл. 1.6).
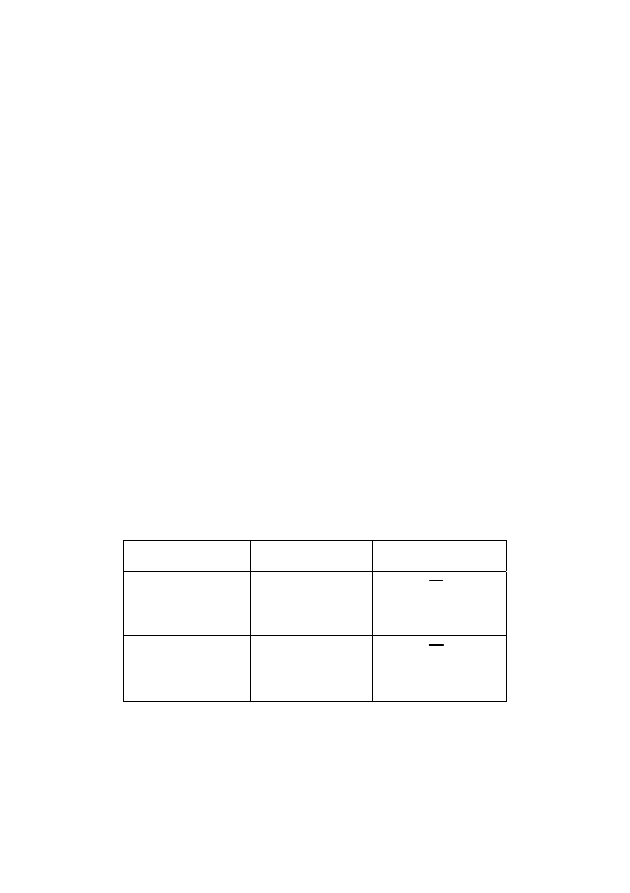
Таблица 1.6
Типы выборок
Повторений
элементов нет
Повторения
элементов есть
Порядок важен
A
r
n
размещения
A
r
n
размещения
с повторениями
Порядок не важен
C
r
n
сочетания
C
r
n
сочетания
с повторениями
Пример. Определяя трех победителей олимпиады среди 20 участников,
мы составляем размещения из 20 элементов по 3, т.к. порядок в этом списке
важен (первое, второе, третье место), и ни одна фамилия не может появиться в
нем дважды.