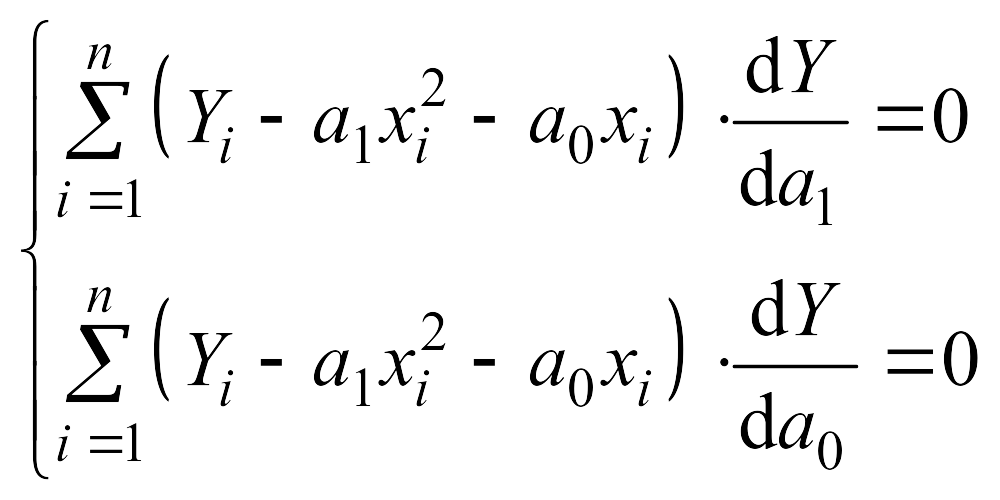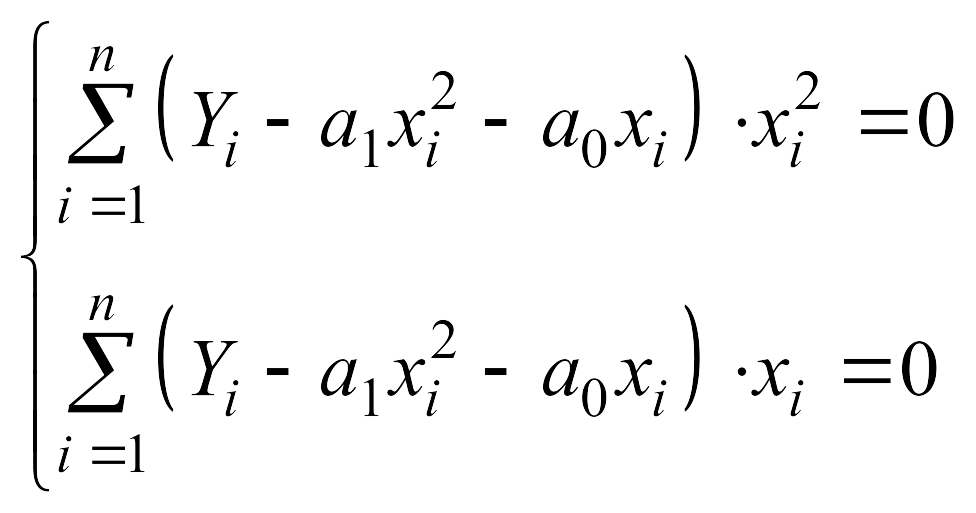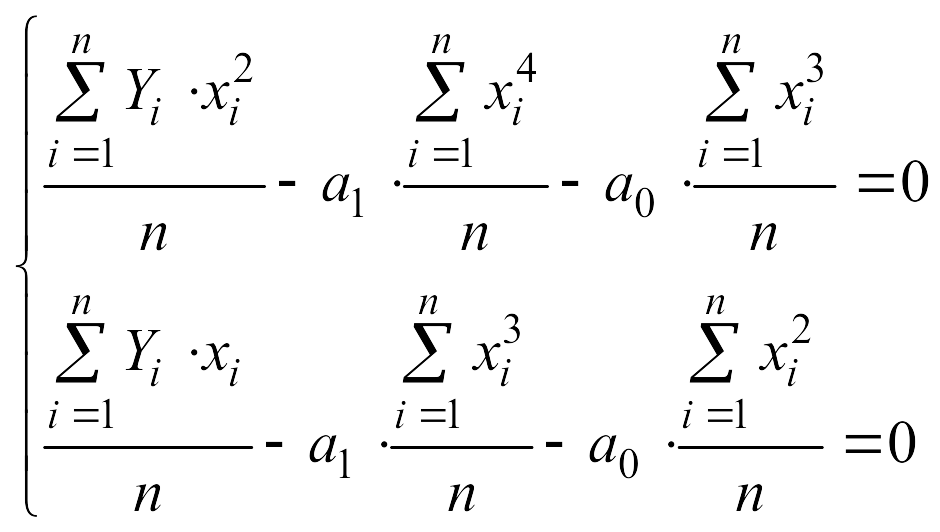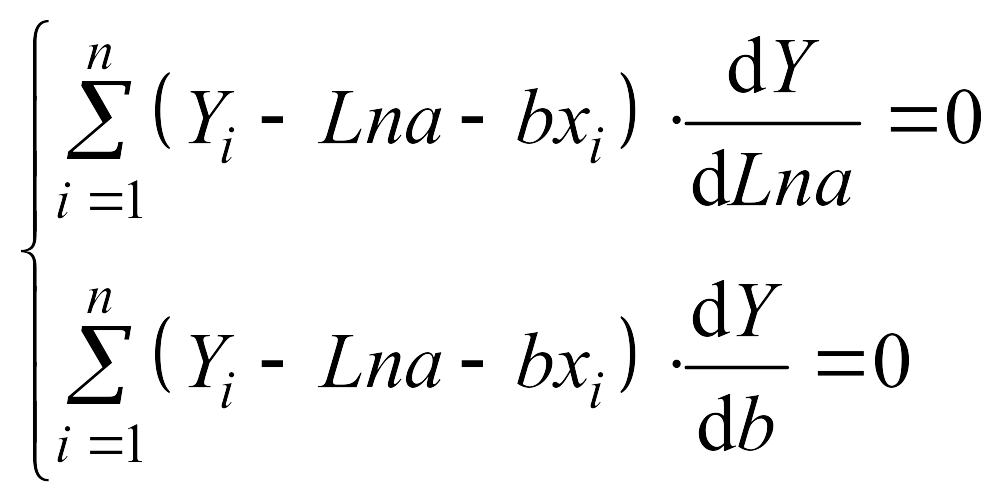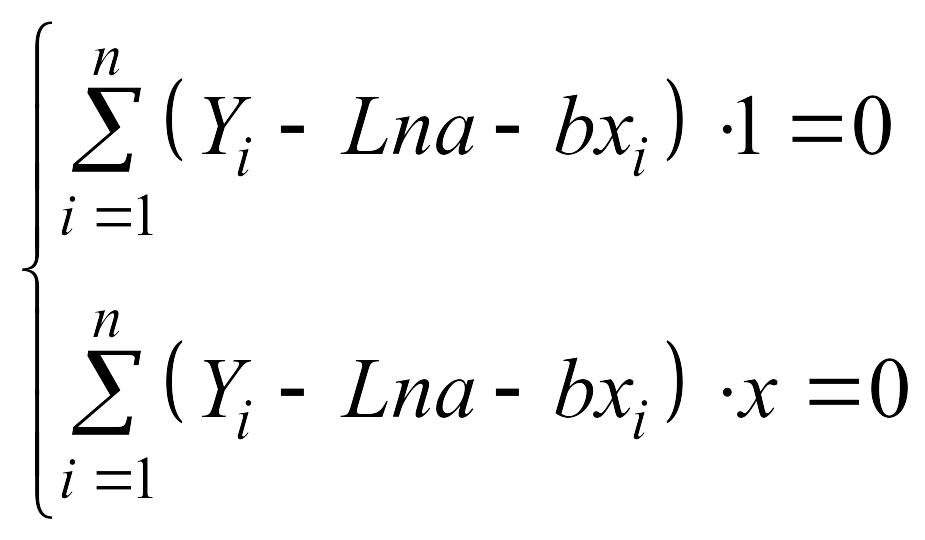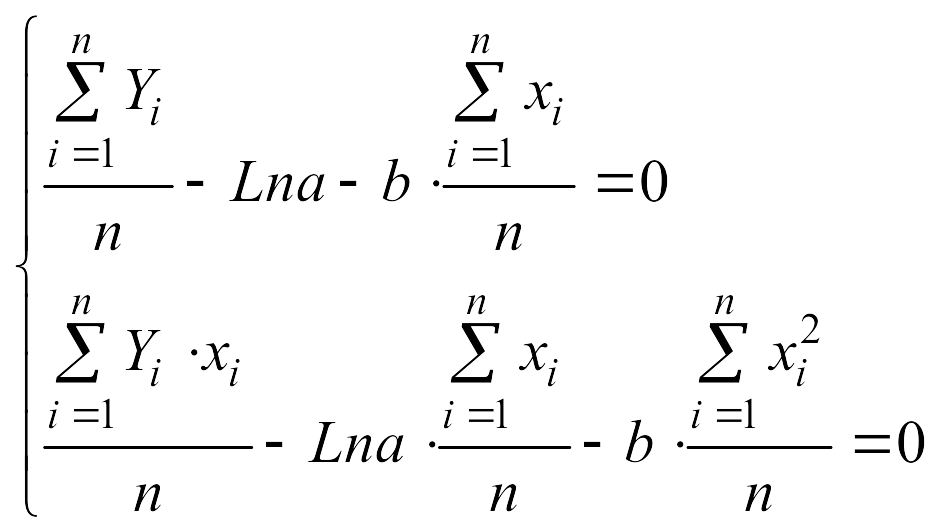Добавлен: 31.01.2019
Просмотров: 1868
Скачиваний: 8
![]()
![]()
Определяем среднее время ожидания в очереди автомобилем, не получившим отказ, час.:
![]()
![]()
Определяем среднее время пребывания автомобиля в системе, час.:
![]()
![]()
Основные числовые характеристики функционирования АТП при n = 2 определены. В дальнейшем для построения графика оптимизации нам потребуются суммарные значения затрат, руб.:
![]()
![]()
Порядок вычисления вероятностей состояний и основных характеристик СМО закрытых ремонтных предприятий с универсальными постами при n = 3, 4 и т. д. аналогичен представленному выше.
Задание
Автотранспортное
предприятие имеет в своем составе N
автомобилей. Среднесуточный пробег
автомобилей составляет L
километров. Периодичность проведения
технического обслуживания № 1 составляет
3000 км, технического обслуживания № 2 –
9000 км. Посты для выполнения ТО – 1,2
являются универсальными. Автомобили
работают 280 дней в году. Среднее время
обслуживания автомобиля при ТО–1
составляет
![]() а при ТО–2
а при ТО–2
![]()
Определить оптимальное количество постов для проведения технического обслуживания и характеристики работы автотранспортного предприятия (с построением графика).
При расчете экономических характеристик СМО учесть, что стоимость простоя одного автомобиля в течение единицы времени составляет – Спр. а, руб.; затраты, связанные с простоем одного канала в течение единицы времени – СПР, руб.; расход средств на выплату зарплаты рабочим постов за единицу времени – СЗП, руб.
Дополнительные исходные данные для расчета выбрать по табл. 3.2.
Таблица 3.2
|
Таблица вариантов заданий |
|||||||
|
|
|||||||
|
Вариант |
N |
L, км |
|
|
Спр. а, руб. |
СПР, руб. |
СЗП, руб. |
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
12 |
472 |
0,96 |
1,85 |
120 |
48 |
66 |
|
|
2 |
14 |
484 |
1,12 |
2,16 |
155 |
62 |
85 |
|
3 |
15 |
490 |
1,20 |
2,31 |
160 |
64 |
88 |
|
4 |
17 |
502 |
1,36 |
2,62 |
210 |
84 |
116 |
|
5 |
25 |
553 |
2,04 |
3,93 |
250 |
100 |
138 |
|
6 |
19 |
514 |
1,52 |
2,93 |
180 |
72 |
99 |
|
7 |
22 |
532 |
1,76 |
3,39 |
165 |
66 |
91 |
|
8 |
24 |
544 |
1,92 |
3,70 |
230 |
92 |
127 |
|
9 |
13 |
583 |
2,44 |
4,70 |
280 |
112 |
154 |
|
10 |
24 |
544 |
1,92 |
3,70 |
115 |
46 |
63 |
|
11 |
25 |
400 |
1,19 |
3,00 |
145 |
58 |
80 |
|
12 |
23 |
420 |
1,25 |
3,15 |
190 |
76 |
105 |
|
13 |
26 |
330 |
0,98 |
2,48 |
250 |
100 |
138 |
|
14 |
15 |
370 |
1,10 |
2,78 |
280 |
112 |
154 |
|
15 |
17 |
290 |
0,57 |
1,43 |
270 |
108 |
149 |
|
16 |
22 |
280 |
0,54 |
1,35 |
150 |
60 |
83 |
|
17 |
18 |
270 |
0,80 |
2,03 |
193 |
77 |
106 |
|
18 |
19 |
360 |
1,07 |
2,70 |
199 |
80 |
109 |
|
19 |
20 |
240 |
0,71 |
1,80 |
262 |
105 |
144 |
|
20 |
28 |
280 |
0,83 |
2,10 |
312 |
125 |
172 |
|
21 |
24 |
368 |
1,43 |
1,91 |
224 |
90 |
123 |
|
22 |
26 |
444 |
1,51 |
2,01 |
206 |
82 |
113 |
|
23 |
14 |
534 |
1,70 |
2,28 |
287 |
115 |
158 |
|
24 |
16 |
544 |
1,51 |
2,01 |
349 |
140 |
192 |
|
25 |
19 |
482 |
1,55 |
2,06 |
143 |
57 |
79 |
|
26 |
15 |
510 |
1,78 |
2,38 |
181 |
72 |
100 |
|
27 |
17 |
607 |
1,05 |
1,40 |
237 |
95 |
130 |
|
28 |
17 |
483 |
1,13 |
1,51 |
312 |
125 |
172 |
|
29 |
21 |
378 |
1,23 |
1,64 |
349 |
140 |
192 |
|
30 |
28 |
406 |
1,47 |
1,96 |
336 |
134 |
185 |
Контрольные вопросы
1. Отличия закрытых систем массового обслуживания от открытых систем.
2. Параметры закрытых СМО: интенсивность потока заявок, интенсивность обслуживания, количество постов ожидания.
3. Вероятностные характеристики СМО: вероятность простоя СМО, вероятность, что будет занято k каналов обслуживания, вероятность отказа в обслуживании, вероятность обслуживания.
4. Абсолютные характеристики СМО: абсолютная пропускная способность, максимальная пропускная способность, средняя длина очереди, среднее число занятых каналов, среднее число свободных каналов, среднее время ожидания обслуживания, среднее время пребывания заявки в СМО.
5. Экономические характеристики СМО.
6. Оптимизация числа обслуживающих каналов.
Практическая работа № 4
ОПТИМИЗАЦИЯ НОМЕНКЛАТУРЫ ЗАПАСНЫХ ЧАСТЕЙ
Цели:
– изучение номенклатуры запасных частей, входящих в группы А, В, С;
– научиться определять единый стоимостной и относительный стоимостный показатели для каждой запасной части;
– научиться определять номенклатуру запасных частей, входящих в группы А, В, С аналитическим методом.
Теоретические сведения
Хранить все выпускаемые в качестве запасных частей детали у дилера, и тем более на АТП (СТО), нерационально. Это приведет к значительному увеличению запасов, росту складских площадей и, самое главное, к неэффективному использованию запасов – большая их часть останется лежать «мертвым грузом». С другой стороны, поскольку отказы деталей носят случайный характер, то теоретически в любой момент может понадобиться любая из запасных частей.
Под номенклатурой запасных частей понимается перечень наименований элементов автомобиля, составленных в определенной последовательности в соответствии с технической документацией предприятий-изготовителей.
Определение номенклатуры запасных частей и объемов хранения на складах разного уровня осуществляется различными методами. В основу наиболее распространенного положено деление всей номенклатуры запасных частей для каждой модели автомобиля по частоте спроса на группы А, В и С. Согласно данному методу вся номенклатура деталей конкретной модели автомобиля (с точки зрения спроса на них) делится на группы А, В, С: первая группа А – детали высокого спроса, В – среднего и С – детали редкого спроса.
Номенклатуру групп А, В, С можно определить с использованием графического и аналитического методов расчетов. Графический метод расчета прост в использовании, но имеет значительную погрешность.
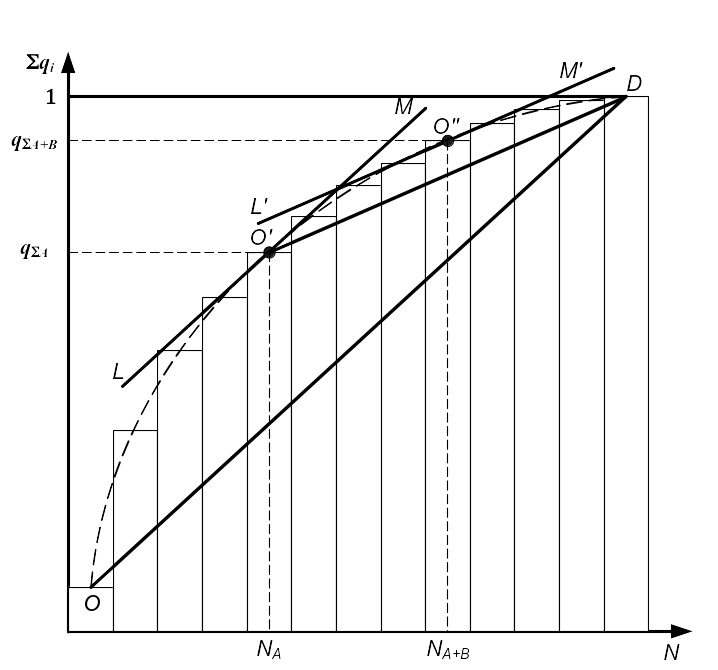
При
графическом способе
(рис. 4.1) на оси ординат наносятся значения
![]() ,
на оси абсцисс – индексы 1, 2, ..., i,
..., N,
соответствующие присвоенным номерам
позиций номенклатуры запасных частей.
,
на оси абсцисс – индексы 1, 2, ..., i,
..., N,
соответствующие присвоенным номерам
позиций номенклатуры запасных частей.
Точки с координатами
![]() на графике соединяются плавной кривой
OO'D, которая в общем случае является
выпуклой. Затем проводится касательная
LМ к кумулятивной кривой OO'D,
параллельно прямой OD.
на графике соединяются плавной кривой
OO'D, которая в общем случае является
выпуклой. Затем проводится касательная
LМ к кумулятивной кривой OO'D,
параллельно прямой OD.
Прямая OD соответствует равномерному распределению затрат по всей номенклатуре, т. е. характеризует долю «определенной» детали в общем показателе:
![]()
|
|
|
|
|
Рис. 4.1. Определение номенклатуры групп АВС |
Абсцисса точки
касания О', округленная до ближайшего
целого значения, отделяет от всей
номенклатуры деталей первую группу NA
(группа А), в которую входят детали
с показателями
![]()
Соответственно
ордината точки О' –
![]() – указывает долю группы деталей в общем
показателе
– указывает долю группы деталей в общем
показателе
![]()
Продолжим деление на группы оставшейся номенклатуры деталей, воспользовавшись вышеописанным приемом. Соединим точку О' с точкой D и проведем касательную к кривой О'O"D, параллельную прямой О'D.
Абсцисса точки касания О'' делит оставшуюся номенклатуру деталей также на две группы: группа В и группа С.
Доля оставшейся «осредненной» детали составит:
![]()
где NA – число деталей (номенклатура) группы А.
Таким образом, в
группу В попадают детали с показателем
![]() ,
подчиняющимся неравенству:
,
подчиняющимся неравенству:
![]()
Следует указать, что если кривая OO'О"D не выпуклая, то невозможно выделить ни одну из групп деталей; если кривая O'O"D выпуклая, то невозможно выделить группы В и С.
Аналитический способ расчета позволяет определять номенклатуру групп с необходимой точностью и включает в себя несколько этапов.
На первом этапе расчетов вводится единый стоимостный показатель, отражающий все виды затрат, связанных с i-й запасной частью. Данный показатель рассчитывается для каждой детали с использованием формулы:
![]()
где Мi – количество i-х деталей, израсходованных за определенный интервал времени (или пробег автомобиля), шт; CЗЧi – стоимость i-й детали, руб.; CТЭi – стоимость трудозатрат на устранение отказа i-й детали, руб.; CПi – потери прибыли предприятия, связанные с простоем автомобиля в ремонте, в частности, из-за отсутствия i-й запасной части, руб.
Полученные значения Ci ранжируются, располагаясь в убывающей последовательности:
![]()
Затем производится присвоение новых индексов: а = 1, b = 2, ..., т = N, где N – общее количество наименований деталей (номенклатура):
![]()
Для удобства расчетов на втором этапе вводятся относительные величины рассматриваемых стоимостных показателей qi (в процентах), тем самым производим нормирование показателей:
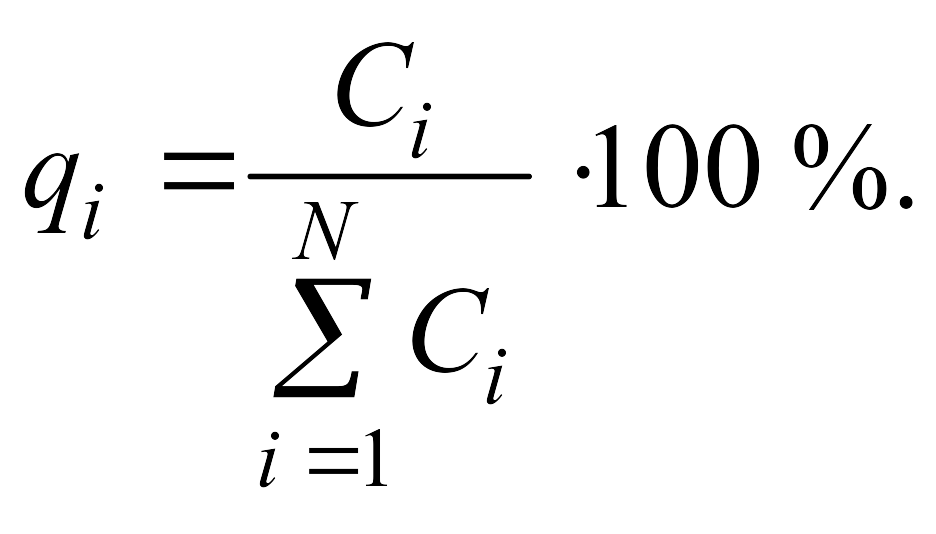
Для удобства
расчетов количество деталей N
целесообразно нормировать в интервале
0–1 и ввести аргумент х. Величины qi
суммируются нарастающим итогом
![]() и представляются в табличной форме в
виде пар значений
и представляются в табличной форме в
виде пар значений
![]() для подбора аналитической зависимости.
для подбора аналитической зависимости.
В большинстве случаев используются две нелинейные зависимости:
![]()
![]()
Выбор той или иной зависимости зависит от значения коэффициента корреляции (чем он выше, тем точнее зависимость).
На
третьем этапе определяем коэффициенты
зависимостей (a0,
a1,
a,
b)
с использованием метода наименьших
квадратов (МНК). При определении
коэффициентов необходимо соблюдать
начальные условия: первое – при х
= 0,
![]() = 0; второе – при х
= 1,
= 0; второе – при х
= 1,
![]() = 1.
= 1.
Методика определении коэффициентов представлена в табл. 4.1.
Таблица 4.1
Методика определения коэффициентов зависимостей
|
Этапы методики |
Зависимость
|
Зависимость
|
|
1. Преобразуем выражение |
|
|
|
2. Определим производные функции по коэффициентам |
|
|
|
3. Составим систему уравнений |
|
|
Продолжение табл. 4.1
|
4. Решаем систему уравнений методом Крамера |
|
|
Для определения координат точки О' (рис. 4.1) воспользуемся теоремой Лагранжа, согласно которой:
![]() (4.1)
(4.1)
где f' (x) – производная функции f (x) в точке касания; f (B), f (A) – значения функции f (x) в начальной и конечной точках.
Решив уравнение (4.1) относительно хA, определим абсциссу и далее переходим к номенклатуре по формуле:
![]()
которая делит номенклатуру на две группы.
Вводим
новую систему координат, принимая за
начало отсчета абсциссу xA
и ординату
![]() (xA).
В некоторых случаях с целью унификации
расчета шкалы по осям могут быть вновь
отнормированы. Таким образом, основное
уравнение (4.1) записывается в виде:
(xA).
В некоторых случаях с целью унификации
расчета шкалы по осям могут быть вновь
отнормированы. Таким образом, основное
уравнение (4.1) записывается в виде:
![]() (4.2)
(4.2)
Пример. В результате анализа расходования запасных частей на предприятии были получены следующие данные (табл. 4.2).
Таблица 4.2
|
Исходные данные |
||||||||||
|
|
||||||||||
|
Номер запасной части |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
qi |
0,5 |
0,2 |
0,1 |
0,063 |
0,05 |
0,05 |
0,014 |
0,01 |
0,01 |
0,003 |
Для проведения расчетов отнормируем величину аргумента, а также просуммируем значение qi с нарастающим итогом (табл. 4.3)
Таблица 4.3
Отнормированные исходные данные
|
Величина аргумента х |
0,1 |
0,2 |
0,3 |
0,4 |
0,5 |
0,6 |
0,7 |
0,8 |
0,9 |
1 |
|
|
0,5 |
0,7 |
0,8 |
0,863 |
0,913 |
0,963 |
0,977 |
0,987 |
0,997 |
1 |
Используя метод наименьших квадратов, выполнив предварительно соответствующие преобразования, находим параметры зависимостей:
![]() – а0
=
2,4585; а1
= –1,4998,
– а0
=
2,4585; а1
= –1,4998,
![]() – а
=
0,7328; b
= 0,2688.
– а
=
0,7328; b
= 0,2688.
Результаты расчетов
значений
![]() по приведенным аналитическим зависимостям
приведены в табл. 4.4.
по приведенным аналитическим зависимостям
приведены в табл. 4.4.
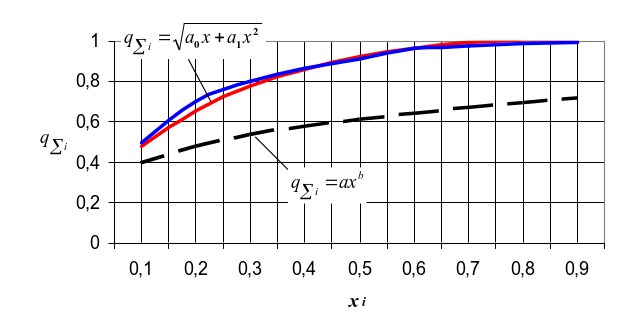
По результатам расчетов построен график (рис. 4.2).
Как видно из рис.
4.2 степенная зависимость (черная
прерывистая линия) не точно описывает
имеющиеся исходные данные (синяя линия).
Таким образом, в качестве аналитической
зависимости принимаем первую функцию
(красная линия)
![]()
|
|
|
Рис.
4.2. Изменение
|
Для расчета абсциссы точки касания воспользуемся уравнением (4.1). Поскольку с одной стороны
![]()
а с другой стороны по теореме Лагранжа
![]()
(получается подстановкой в уравнение (4.1) значений функции и аргумента в начальных и конечных точках, т. е. при х = 0, у = 0 и при х = 1, у = 1), получим
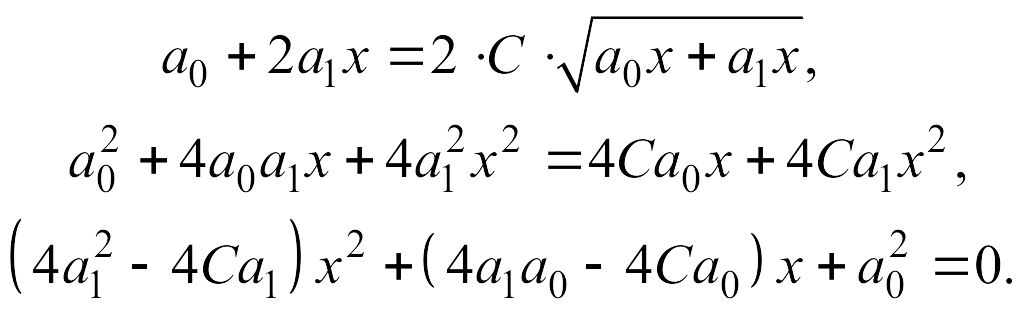
В результате решения квадратного уравнения, с подстановкой в него уже определенных коэффициентов, получим два корня – x1 = 1,28 и x2 = 0,3. Так как значение аргумента не может быть больше единицы, то истинным корнем является xA = x2 = 0,3.
Подставив полученное значение аргумента в исходную аналитическую зависимость, получим относительную стоимостную оценку деталей группы А:
![]()
Полученные значения указывают координаты точки О' – границы группы А (рис. 4.1). Домножив xA = 0,3 на количество (номенклатуру) деталей данного узла N, получим количественную оценку числа наименований деталей группы А.
Определим координаты точки О". При подстановке xA = 0,3, qA = 0,755 в формулу (4.2), находим
![]()
Затем по формуле
![]()
получим x = xA+B = 0,45 и qA+B = 0,88.
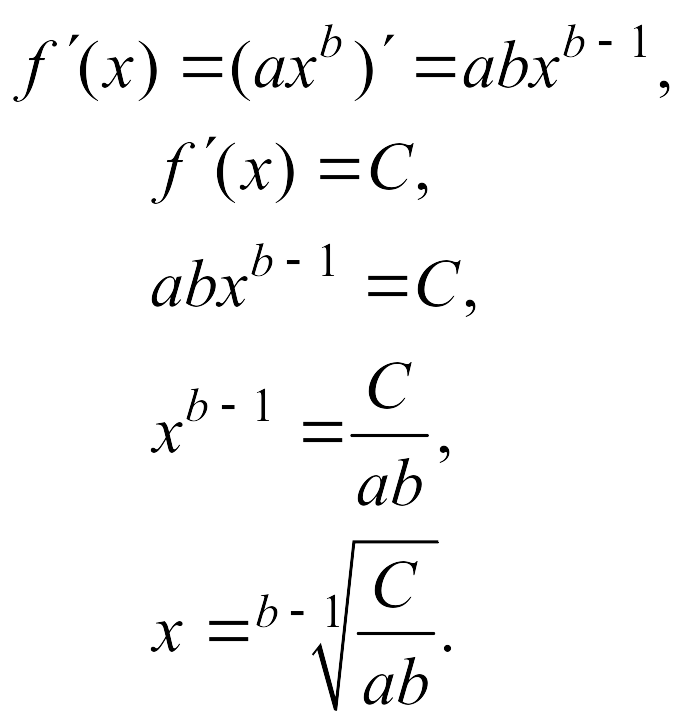
Если
в качестве зависимости будет выбрана
функция
![]() ,
то методика оценивания номенклатуры
групп будет иметь следующие позиции:
,
то методика оценивания номенклатуры
групп будет иметь следующие позиции:
Задание
По результатам анализа расхода запасных частей были получены данные по значениям единого стоимостного показателя (Ci) для различных деталей автомобиля (табл. 4.5 и 4.6). Исходя из имеющейся информации, определить номенклатуру запасных частей входящих в группы A, B, C используя аналитический метод расчета.
Таблица 4.5
|
Таблица вариантов заданий |
|||||||||||||||
|
|
|||||||||||||||
|
Номер элемента |
Номера вариантов |
||||||||||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
|
|
Значение единого стоимостного показателя (Ci), руб. |
|||||||||||||||
|
1 |
16340 |
40850 |
15712 |
9078 |
15712 |
23856 |
36765 |
18854 |
3631 |
32994 |
2623 |
7439 |
6840 |
848 |
3815 |
|
2 |
13440 |
33600 |
12923 |
7467 |
12923 |
19622 |
30240 |
15508 |
2987 |
27138 |
11426 |
32400 |
29793 |
3692 |
16615 |
|
3 |
33287 |
38280 |
30381 |
6076 |
6600 |
48599 |
34452 |
36457 |
2430 |
13860 |
15468 |
35280 |
13635 |
2703 |
14193 |
|
4 |
40174 |
46200 |
36667 |
7333 |
7966 |
58654 |
41580 |
44000 |
2933 |
16728 |
9861 |
22491 |
8692 |
1723 |
9048 |
|
5 |
3717 |
18585 |
7744 |
3204 |
2950 |
5427 |
16727 |
9293 |
1282 |
6195 |
15184 |
27144 |
10081 |
2567 |
9179 |
|
6 |
9760 |
48800 |
20333 |
8414 |
7746 |
14250 |
43920 |
24400 |
3366 |
16267 |
12778 |
22842 |
8484 |
2160 |
7724 |
|
7 |
9913 |
22800 |
8143 |
5429 |
4851 |
14473 |
20520 |
9771 |
2171 |
10187 |
5769 |
14580 |
7336 |
2314 |
8953 |
|
8 |
11409 |
26240 |
9371 |
6248 |
5583 |
16657 |
23616 |
11246 |
2499 |
11724 |
11481 |
29016 |
14599 |
4606 |
17817 |
|
9 |
15053 |
28600 |
8171 |
22880 |
17333 |
21977 |
25740 |
9806 |
9152 |
36400 |
19672 |
46080 |
16168 |
11378 |
63247 |
|
10 |
11116 |
21120 |
6034 |
16896 |
12800 |
16229 |
19008 |
7241 |
6758 |
26880 |
5394 |
12636 |
4434 |
3120 |
17344 |
|
11 |
8800 |
39600 |
9659 |
10732 |
11647 |
12848 |
35640 |
11590 |
4293 |
24459 |
9062 |
16200 |
8120 |
1565 |
7714 |
|
12 |
4500 |
20250 |
4939 |
5488 |
5956 |
6570 |
18225 |
5927 |
2195 |
12507 |
3464 |
6192 |
3104 |
598 |
2949 |
|
13 |
768 |
5220 |
1864 |
932 |
2747 |
1121 |
4698 |
2237 |
373 |
5769 |
14783 |
21870 |
9113 |
2627 |
19627 |
|
14 |
1094 |
7440 |
2657 |
1329 |
3916 |
1597 |
6696 |
3189 |
531 |
8223 |
14904 |
22050 |
9188 |
2649 |
19788 |
|
15 |
1797 |
8265 |
5700 |
2119 |
1816 |
2623 |
7439 |
6840 |
848 |
3815 |
33666 |
35280 |
19600 |
2703 |
30489 |
|
16 |
7826 |
36000 |
24828 |
9231 |
7912 |
11426 |
32400 |
29793 |
3692 |
16615 |
17039 |
17856 |
9920 |
1368 |
15431 |
|
17 |
10595 |
39200 |
11362 |
6759 |
6759 |
15468 |
35280 |
13635 |
2703 |
14193 |
16340 |
40850 |
15712 |
9078 |
15712 |
|
18 |
6754 |
24990 |
7243 |
4309 |
4309 |
9861 |
22491 |
8692 |
1723 |
9048 |
13440 |
33600 |
12923 |
7467 |
12923 |
|
19 |
10400 |
30160 |
8401 |
6417 |
4371 |
15184 |
27144 |
10081 |
2567 |
9179 |
33287 |
38280 |
30381 |
6076 |
6600 |
|
20 |
8752 |
25380 |
7070 |
5400 |
3678 |
12778 |
22842 |
8484 |
2160 |
7724 |
40174 |
46200 |
36667 |
7333 |
7966 |
|
21 |
3951 |
16200 |
6113 |
5786 |
4263 |
5769 |
14580 |
7336 |
2314 |
8953 |
3717 |
18585 |
7744 |
3204 |
2950 |
|
22 |
7863 |
32240 |
12166 |
11514 |
8484 |
11481 |
29016 |
14599 |
4606 |
17817 |
9760 |
48800 |
20333 |
8414 |
7746 |
|
23 |
13474 |
51200 |
13474 |
28444 |
30118 |
19672 |
46080 |
16168 |
11378 |
63247 |
9913 |
22800 |
8143 |
5429 |
4851 |
|
24 |
3695 |
14040 |
3695 |
7800 |
8259 |
5394 |
12636 |
4434 |
3120 |
17344 |
11409 |
26240 |
9371 |
6248 |
5583 |
|
25 |
6207 |
18000 |
6767 |
3913 |
3673 |
9062 |
16200 |
8120 |
1565 |
7714 |
15053 |
28600 |
8171 |
22880 |
17333 |
|
26 |
2372 |
6880 |
2586 |
1496 |
1404 |
3464 |
6192 |
3104 |
598 |
2949 |
11116 |
21120 |
6034 |
16896 |
12800 |
|
27 |
10125 |
24300 |
7594 |
6568 |
9346 |
14783 |
21870 |
9113 |
2627 |
19627 |
8800 |
39600 |
9659 |
10732 |
11647 |
|
28 |
10208 |
24500 |
7656 |
6622 |
9423 |
14904 |
22050 |
9188 |
2649 |
19788 |
4500 |
20250 |
4939 |
5488 |
5956 |
|
29 |
23059 |
39200 |
16333 |
6759 |
14519 |
33666 |
35280 |
19600 |
2703 |
30489 |
768 |
5220 |
1864 |
932 |
2747 |
|
30 |
11671 |
19840 |
8267 |
3421 |
7348 |
17039 |
17856 |
9920 |
1368 |
15431 |
1094 |
7440 |
2657 |
1329 |
3916 |