Окончание табл. 1.5

Контрольные вопросы

1. Понятия теории массового обслуживания: система массового обслуживания, канал обслуживания, стационарный поток, ординарный поток.

2. Параметры СМО: интенсивность потока заявок, интенсивность обслуживания, количество постов ожидания.

3. Вероятностные характеристики СМО: вероятность простоя СМО, вероятность, что будет занято k каналов обслуживания, вероятность отказа в обслуживании, вероятность обслуживания.

4. Абсолютные характеристики СМО: абсолютная пропускная способность, максимальная пропускная способность, средняя длина очереди, среднее число занятых каналов, среднее число свободных каналов, среднее время ожидания обслуживания, среднее время пребывания заявки в СМО.

5. Экономические характеристики СМО.

6. Оптимизация числа обслуживающих каналов.

Практическая работа № 2

РАСЧЕТ МНОГОКАНАЛЬНОЙ СМО

СО СПЕЦИАЛИЗИРОВАННЫМИ ПОСТАМИ

Цели:

– научиться определять технические параметры и характеристики разомкнутых СМО со специализированными постами;

– научиться определять экономические характеристики разомкнутых СМО со специализированными постами;

– научиться определять оптимальную численность специализированных рабочих постов (каналов обслуживания).

Теоретические сведения

Специализированными называются такие посты, на которых выполняются однородные работы или работы по обслуживанию и ремонту отдельных агрегатов автомобиля.

Основным отличием расчета СМО со специализированными постами от расчета СМО с универсальными постами является то, что он ведется отдельно для каждого элемента. То есть необходимо определить оптимальное число постов, обслуживающих каждый элемент в отдельности. Это связано с тем, что пост специализируется на обслуживании и ремонте конкретного элемента, и даже если он свободен, он не может принять автомобиль с заявкой на обслуживание другого элемента (например, пост по регулированию углов установки управляемых колес или окрасочная камера).

Методика расчета СМО со специализированными постами не отличается от методики расчета СМО с универсальными постами, кроме того, что в расчет вместо величин и по всем элементам необходимо подставлять значения и по каждому рассчитываемому элементу (например, для примера, приведенного в практической работе № 1 для первого элемента и ).

Как и при расчете СМО с универсальными постами, значением параметра необходимо задаваться, начиная с одного.

Задание

Определить с использованием теории массового обслуживания оптимальное количество постов и характеристики работы станции технического обслуживания автомобилей со специализированными постами и ограничением на длину очереди (с построением графика). СТОА выполняет пять видов работ (работа по пяти элементам). Режим работы: десятичасовой рабочий день. СТОА имеет один пост ожидания.

При расчете в качестве исходных данных использовать исходные данные первой практической работы.

Контрольные вопросы

1. Понятие «специализированный пост». Отличия специализированных постов от универсальных.

2. Порядок выбора (расчета) параметров СМО со специализированными постами.

3. Отличие методики расчета характеристик и оптимизации СМО со специализированными постами от методики расчета СМО с универсальными постами.

Практическая работа № 3

РАСЧЕТ МНОГОКАНАЛЬНОЙ СМО

ЗАКРЫТЫХ РЕМОНТНЫХ ПРЕДПРИЯТИЙ (ЗАКРЫТОЙ СМО)

Цели:

– научиться определять технические параметры и характеристики замкнутых СМО;

– научиться определять экономические характеристики замкнутых СМО;

– научиться определять оптимальную численность рабочих постов (каналов обслуживания) замкнутых СМО.

Теоретические сведения

Наряду с открытыми системами, примером которой являются рассмотренные в предыдущих практических работах СМО, в практике имеются так называемые закрытые ремонтные предприятия, т. е. ремонтные мастерские (зоны или посты Технического обслуживания и Текущего ремонта) на территории какого-либо автомобильного объединения.

Отличительной чертой указанных ремонтных мастерских является то, что они не принимают посторонние заявки, а обслуживают только подвижной состав данного предприятия. При этом прибывшая заявка (автомобиль) не покидает очереди до тех пор, пока не будет обслужена.

До сих пор мы рассматривали только такие системы массового обслуживания, для которых интенсивность  входящего потока заявок не зависит от состояния системы. В этом случае источник заявок является внешним по отношению к СМО и генерирует неограниченный поток требований. Рассмотрим системы массового обслуживания, для которых  зависит от состояния системы, при чем источник требований является внутренним и генерирует ограниченный поток заявок.

Например, обслуживается автомобильный парк, состоящий из N машин, на n постах (N > n), причем посты являются универсальными, каждый автомобиль обслуживается только на одном посту. Здесь автомобили являются источниками требований (заявок на обслуживание), а посты – обслуживающими каналами. Неисправный автомобиль после обслуживания используется по своему прямому назначению и становится потенциальным источником возникновения требований на обслуживание. Очевидно, что интенсивность  зависит от того, сколько автомобилей в данный момент находится в эксплуатации (N – k) и сколько автомобилей обслуживается или стоит в очереди, ожидая обслуживания (k).

В рассматриваемой модели емкость источника требований следует считать ограниченной. Входящий поток требований исходит из ограниченного числа эксплуатируемых автомобилей (N – k), которые в случайные моменты времени отказывают и требуют обслуживания.

При этом каждый автомобиль из (N – k) находится в эксплуатации и генерирует поток требований с определенной интенсивностью независимо от других объектов. Требование, поступившее в систему в момент, когда свободен хотя бы один канал, немедленно идет на обслуживание. Если требование застает все каналы занятыми обслуживанием других требований, то оно не покидает систему, а становится в очередь и ждет, пока один из каналов не станет свободным.

Таким образом, в замкнутой СМО входящий поток требований формируется из выходящего.

Технические параметры и характеристики СМО

Параметры закрытой СМО определяются аналогично параметрам разомкнутой СМО в зависимости от вида постов.

Таким образом, исходными данными для расчета являются: количество каналов (n), среднее время обслуживания заявки в канале ( ), интенсивность потока заявок () – среднее количество заявок, поступающих в СМО в единицу времени, а также количество автомобилей, эксплуатируемых АТП (N).

В качестве характеристик закрытых СМО обычно используются следующие величины:

Р_k – вероятность k-го состояния:

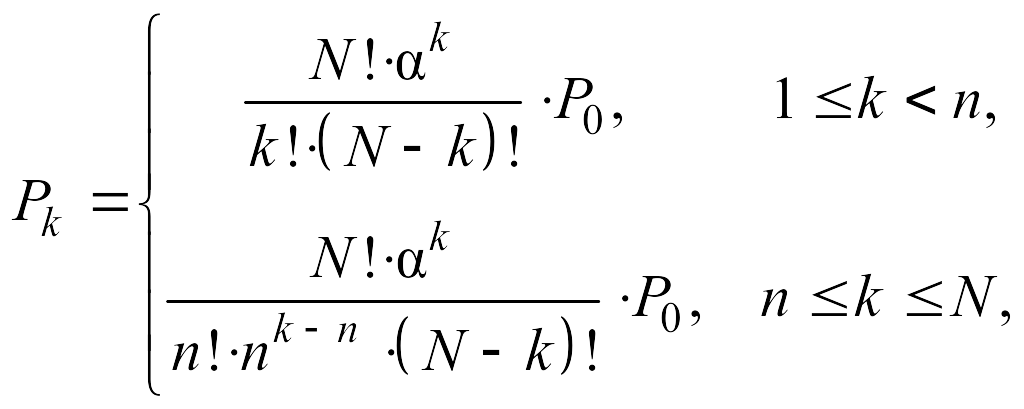
где k – число заявок, находящихся в очереди или на обслуживании;  – плотность процесса; Р₀ – вероятность того, что все каналы обслуживания свободны (находятся в состоянии простоя).

Величина Р₀ показывает, какую часть от общего времени работы СМО все ее каналы свободны, и определяется из условия нормирования полученных результатов.

Р_отк – вероятность отказа в обслуживании. Очевидно, что для замкнутой СМО вероятность отказа в обслуживании равна 0, а вероятность обслуживания или относительная пропускная способность (Р_отн) равна 1.

Q_абс – абсолютная пропускная способность (среднее количество заявок, обслуживаемых в единицу времени):

Q_макс – максимально возможная пропускная способность СМО:

М[S] – среднее число заявок в очереди (средняя длина очереди):

М[γ] – среднее число свободных каналов:

М[K] – среднее число заявок на обслуживании (в каналах), или среднее число занятых каналов:

K_прост – коэффициент простоя каналов:

K_занят – коэффициент занятости каналов:

– среднее число заявок в СМО, т. е. на обслуживании и в очереди:

β_прост – коэффициент простоя обслуживаемого объекта (машины) в очереди:

β_занят – коэффициент использования объектов (машин):

t_{ср. ожид} – среднее время пребывания заявки в очереди (среднее время ожидания обслуживания):

t_сум – среднее время пребывания заявки в СМО, т. е. в очереди и на обслуживании:

Оптимизация числа обслуживающих постов

Обобщенная формула для решения закрытой задачи, т. е. для многоканальной СМО закрытых ремонтных предприятий, имеет вид:

где С_{пр. а} – стоимость простоя одного автомобиля в течение единицы времени; С_ПР – затраты, связанные с простоем одного канала в течение единицы времени; С_ЗП – расход средств на выплату зарплаты рабочим постов.

Пример. Исследуем функционирование автотранспортного предприятия (АТП). Требуется определить числовые характеристики функционирования АТП и определить оптимальное количество постов, при котором его работа будет давать наибольший экономический эффект.

Исходными данными для расчета являются: количество каналов (n), среднее время обслуживания заявки в канале ( ), интенсивность потока заявок (), так как рассматриваемая модель обслуживания машинного парка представляет собой модель замкнутой системы массового обслуживания, то для расчета нам также необходимо знать количество автомобилей, эксплуатируемых АТП (N). Значением параметра n будем задаваться.

Для определения исходных данных нам необходимы статистические данные о количестве заездов автомобилей. Для примера воспользуемся данными, приведенными в примере для практической работы № 1 при расчете открытой СМО.

Примем, что рабочие посты рассчитываемого АТП универсальные и на них выполняют обслуживание и ремонт 5 элементов. Исходя из имеющихся данных, мы определяли _общ:

Необходимо отметить, что в качестве элементов обслуживания могут выступать различные виды ТО, ТР и планово-предупредительного ремонта. Например, на предприятии имеется 29 автомобилей, со средним среднесуточным пробегом (L_cc) 200 км, периодичностью проведения ТО-1 5000 км, периодичностью проведения ТО-2 15000 км и заданной программой планово-предупредительного ремонта периодичностью 67000 км. Исходя из этого можно получить исходную информацию для расчета закрытой СМО. Для этого определим периодичность заезда каждого автомобиля (в днях): на ТО-1 – 25 дней, на ТО-2 – 75 дней, на ППР – 335 дней. Соответственно ежедневная интенсивность заездов составит: на ТО-1 – 1,16 автомобилей, на ТО-2 – 0,39 автомобилей, на ППР – 0,09 автомобилей. Исходя из этого, можно определить часовую интенсивность заездов, а, зная среднее время обслуживания автомобилей на ТО-1, 2 и ППР, получаем возможность оценить оптимальное количество постов ТО-1, 2 и ППР.

В случае если рабочие посты на АТП будут приняты специализированными, порядок расчета  аналогичен представленному в практической работе № 2.

Распределение статей затрат при работе постов представлено в табл. 3.1.

Таблица 3.1

Распределение статей затрат

В расчетах вместо величины будем использовать интенсивность обслуживания заявок:

и приведенную плотность процесса:

Теперь можно непосредственно приступить к решению поставленной задачи, т. е. определению основных характеристик СМО и оптимизации количества обслуживающих постов.

Поясним порядок вычисления вероятностей состояний и основных характеристик СМО закрытых ремонтных предприятий с универсальными постами при n = 1.

Определим вероятности состояний системы. В связи с тем, что число заявок в очереди и на обслуживании (k) удовлетворяет условию n ≤ k ≤ N, то вероятности состояний системы будем определять всегда по формуле:

Вероятность Р₁ показывает вероятность нахождения одного автомобиля (из всего количества) в очереди или на обслуживании, вероятность Р₂ показывает вероятность нахождения двух автомобилей в очереди или на обслуживании и т. д.

Учитывая, что , и используя результаты расчета Р_k, вычислим Р₀:

откуда вероятность полного простоя одного имеющегося поста обслуживания

Исходя из этого:

Вычисляем абсолютную пропускную способность станции за час работы, авт.:

Вычисляем максимально возможную пропускную способность станции за час работы, авт.:

Определяем математическое ожидание длины очереди, авт.:

Определяем среднее число каналов, простаивающих из-за отсутствия работы:

Вычисляем математическое ожидание числа занятых каналов:

Вычисляем коэффициент простоя каналов:

Вычисляем коэффициент занятости каналов:

Определяем среднее число заявок в СМО:

Определяем коэффициент простоя обслуживаемого объекта в очереди:

Вычисляем коэффициент использования объектов:

Определяем среднее время ожидания в очереди автомобилем, не получившим отказ, час.:

Определяем среднее время пребывания автомобиля в системе, час.:

Основные числовые характеристики функционирования АТП при n = 1 определены. В дальнейшем для построения графика оптимизации нам потребуются суммарные значения затрат, руб.:

Продолжим вычисления при n = 2.

Определим вероятности состояний системы. В связи с тем, что число заявок в очереди и на обслуживании (k) сначала удовлетворяет условию 1  k < n, а потом n  k  N, то вероятности состояний системы будем определять по формуле

Определим вероятность:

а по формуле остальные вероятности:

Учитывая, что и используя результаты расчета Р_k, вычислим Р₀:

откуда вероятность полного простоя одного имеющегося поста обслуживания

Исходя из этого:

Вычисляем абсолютную пропускную способность станции за час работы, авт.:

Вычисляем максимально возможную пропускную способность станции за час работы, авт.:

Определяем математическое ожидание длины очереди, авт.:

Определяем среднее число каналов, простаивающих из-за отсутствия работы:

Вычисляем математическое ожидание числа занятых каналов:

Вычисляем коэффициент простоя каналов:

Вычисляем коэффициент занятости каналов:

Определяем среднее число заявок в СМО:

Определяем коэффициент простоя обслуживаемого объекта в очереди:

Вычисляем коэффициент использования объектов: