Файл: Перельман Я. И. - Занимательная физика. Книга 1 - 1983.pdf
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 20.10.2020
Просмотров: 1569
Скачиваний: 12
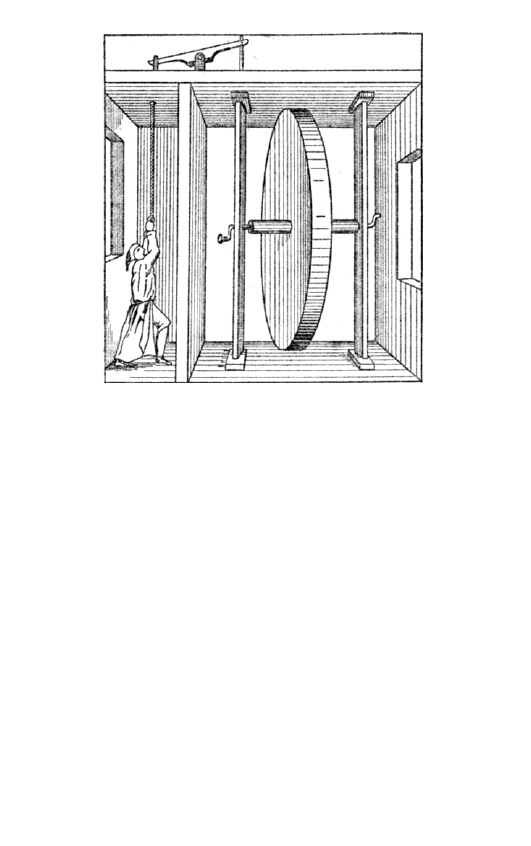
Рис
. 48.
Разоблачение
секрета
колеса
Орфиреуса
.
метно
дергавшими
за
тонкий
шнурок
.
Этими
людьми
были
брат
изобретателя
и
его
служанка
.
Разоблаченный
изобретатель
не
сдавался
;
он
упорно
утверждал
до
самой
смерти
,
что
жена
и
прислуга
донесли
на
него
по
злобе
.
Но
доверие
к
нему
было
подорвано
.
Недаром
он
твердил
посланцу
Петра
,
Шумахеру
,
о
людском
злонра
-
вии
и
о
том
,
что
«
весь
свет
наполнен
злыми
людьми
,
которым
верить
весьма
невозможно
».
Во
времена
Петра
I
славился
в
Германии
еще
и
другой
«
вечный
двигатель
» –
некоего
Гертнера
.
Шумахер
писал
об
этой
машине
следующее
: «
Господина
Гертнера
perpetuum mobile,
который
я
в
Дрездене
видел
,
состоит
из
холста
,
пес
-
ком
засыпанного
,
и
в
образе
точильного
камня
сделанной
машины
,
которая
назад
и
вперед
сама
от
себя
движется
,
но
,
по
словам
господина
ннвентора
(
изобретате
-
ля
),
не
может
весьма
велика
сделаться
».
Без
сомнения
,
и
этот
двигатель
не
дос
-
тигал
своей
цели
и
в
лучшем
случае
представлял
собой
замысловатый
механизм
с
искусно
скрытым
,
отнюдь
не
«
вечным
»
живым
двигателем
.
Вполне
прав
был
Шумахер
,
когда
писал
Петру
,
что
французские
и
английские
ученые
«
ни
во
что
почитают
все
оные
перепетум
мобилес
и
сказывают
,
что
оное
против
нринципи
-
ев
математических
».
54
Г Л А В А
П Я Т А Я
С В О Й С Т В А
Ж И Д К О С Т Е Й
И
Г А З О В
Задача
о
двух
кофейниках
Перед
вами
два
кофейника
одинаковой
ширины
:
один
высокий
,
другой
–
низкий
.
Какой
из
них
вместительнее
?
Многие
,
вероятно
,
не
подумав
,
скажут
,
что
высокий
кофейник
вместительнее
низкого
.
Если
бы
вы
,
однако
,
стали
лить
жидкость
в
высокий
кофейник
,
вы
смогли
бы
налить
в
него
только
до
уровня
отвер
-
стия
его
носика
–
дальше
вода
начнет
выливаться
.
А
так
как
отверстия
носика
у
обоих
кофейников
на
одной
высоте
,
то
низкий
кофейник
оказывается
столь
же
вместительным
,
как
и
высокий
с
коротким
носиком
.
Это
и
попятно
:
в
кофейнике
и
в
трубке
носика
,
как
во
всяких
сообщающихся
сосудах
,
жидкость
должна
стоять
на
одинаковом
уровне
,
несмотря
на
то
что
жидкость
в
носике
весит
гораздо
меньше
,
чем
в
остальной
части
кофейника
.
Если
же
носик
недостаточно
высок
,
вы
никак
не
нальете
кофейник
доверху
:
вода
будет
выливаться
.
Обычно
носик
устраивается
даже
выше
краев
кофейника
,
чтобы
сосуд
можно
было
немного
наклонять
,
не
выливая
содержимого
.
Рис
. 49.
В
какой
из
этих
кофейни
-
в
можно
налить
больше
жидко
сти
?
ко
-
Чего
не
знали
древние
Жители
современного
Рима
до
сих
пор
пользуются
остатками
водопровода
,
построенного
еще
древними
:
солидно
возводили
римские
рабы
водопроводные
сооружения
.
55
Не
то
приходится
сказать
о
познаниях
римских
инженеров
,
руководивших
этими
работами
;
они
явно
недостаточно
были
знакомы
с
основами
физики
.
Взгляните
на
. 50,
воспроизведенный
с
картины
музея
в
Мюнхене
.
Вы
видите
,
что
римский
водопровод
прокладывался
не
в
земле
,
а
над
ней
,
на
высоких
каменных
столбах
.
Для
чего
это
делалось
?
Разве
не
проще
было
бы
прокладывать
в
земле
трубы
,
как
делается
теперь
?
Конечно
,
проще
,
но
римские
инженеры
того
времени
имели
весьма
смутное
представление
о
законах
сообщающихся
сосудов
.
Они
опасались
,
что
в
водоемах
,
соединенных
очень
длинной
трубой
,
вода
не
установится
на
одинаковом
уровне
.
Если
трубы
проло
-
жены
в
земле
,
следуя
уклонам
почвы
,
то
в
некоторых
участках
вода
ведь
должна
течь
вверх
, –
и
вот
римляне
боялись
,
что
вода
вверх
не
потечет
.
Поэтому
они
обычпо
придавали
водопроводным
трубам
равномерный
уклон
вниз
на
всем
их
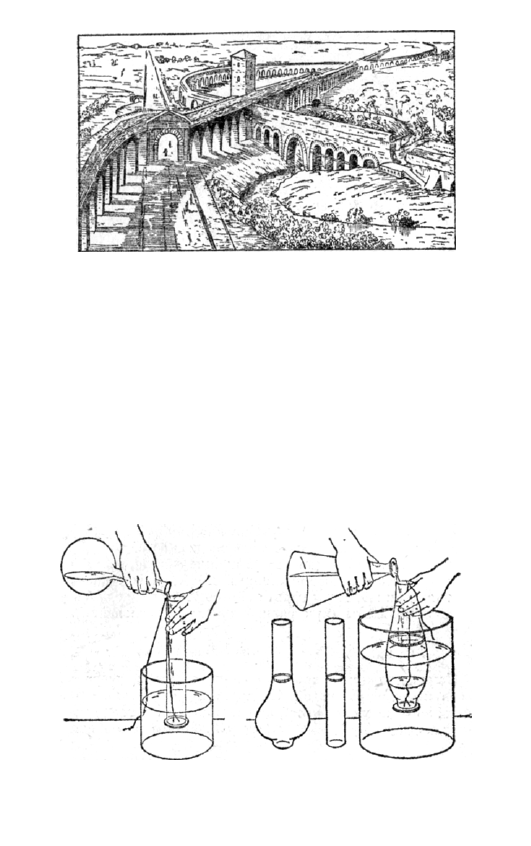
Рис
. 50.
Водопроводные
сооружения
Древнего
Рима
.
пути
(
а
для
этого
требовалось
нередко
либо
вести
воду
в
обход
,
либо
возводить
высокие
арочные
подпоры
)
.
Одна
из
римских
труб
,
Аква
Марциа
,
имеет
длину
100
км
,
между
тем
как
прямое
расстояние
между
ее
концами
вдвое
меньше
.
Полсотни
километров
каменной
кладки
пришлось
проложить
из
-
за
незнания
элементарного
закона
физики
!
Жидкости
давят
...
вверх
!
О
том
,
что
жидкости
давят
вниз
,
на
дно
сосуда
,
и
вбок
,
на
стенки
,
знают
Даже
те
,
кто
никогда
не
изучал
физики
.
Но
что
они
давят
и
вверх
,
многие
даже
не
подозревают
.
Обыкновенное
ламповое
стекло
поможет
убедиться
,
что
такое
давление
действительно
существует
.
Вырежьте
из
плотного
картона
кружок
таких
размеров
,
чтобы
он
закрывал
отверстие
лампового
стекла
.
Приложите
его
к
краям
стекла
и
погрузите
в
воду
,
как
показано
на
Чтобы
кружок
не
отпадал
при
погружении
,
его
можно
придерживать
ниткой
,
протянутой
через
его
Рис
. 51.
Простой
способ
убедиться
,
что
жидкость
давит
снизу
вверх
.
Рис
. 52.
Давление
жидкости
на
дно
сосуда
зависит
от
площади
дна
и
высоты
уровня
жидкости
.
56
57
ни
натяжением
нитки
:
его
подпирает
вода
,
надавливающая
на
него
снизу
вве
и
та
потеря
веса
в
жид
-
кос
отвесный
столб
одинаковой
с
ним
высоты
(
при
равных
площадях
оснований
).
водой
.
На
другую
–
точно
такое
ж
к
дерева
(
рис
. 53).
Какое
ведро
пере
-
первое
ведро
, «
так
колько
весит
все
в
стакан
с
водой
.
Что
сделается
с
весами
,
когда
гирька
упадет
на
дно
со
-
суда
?
центр
,
или
просто
прижать
пальцем
.
Погрузив
стекло
до
определенной
глубины
,
вы
заметите
,
что
кружок
хорошо
держится
и
сам
,
не
прижимаемый
ни
давлением
пальца
,
рх
.
Вы
можете
даже
измерить
величину
этого
давления
вверх
.
Наливайте
осторожно
в
стекло
воду
;
как
только
уровень
ее
внутри
стекла
приблизится
к
уровню
в
сосуде
,
кружок
отпадет
.
Значит
,
давление
воды
на
кружок
снизу
уравновешивается
давлением
на
него
сверху
столба
воды
,
высота
которого
равна
глубине
кружка
под
водой
.
Таков
закон
давления
жидкости
на
всякое
погруженное
тело
.
Отсюда
,
между
прочим
,
происходит
тях
,
о
которой
говорит
знаменитый
закон
Архимеда
.
Имея
несколько
ламповых
стёкол
разной
формы
,
но
с
одинаковыми
отвер
-
стиями
,
вы
сможете
проверить
и
другой
закон
,
относящийся
к
жидкостям
именно
:
давление
жидкости
на
дно
сосуда
зависит
только
от
площади
дна
и
вы
-
соты
уровня
,
от
формы
же
сосуда
оно
совершенно
не
зависит
.
Проверка
будет
состоять
в
том
,
что
вы
проделаете
описанный
сейчас
опыт
с
разными
стеклами
,
погружая
их
на
одну
и
ту
же
глубину
(
для
чего
надо
предварительно
приклеить
к
стеклам
бумажные
полоски
на
равной
высоте
).
Вы
заметите
,
что
кружок
всякий
раз
будет
отпадать
при
одном
и
том
же
уровне
воды
в
стеклах
Значит
,
давление
водяных
столбов
различной
формы
одинаково
,
если
только
одинаковы
их
основание
и
высота
.
Обратите
внимание
на
то
,
что
здесь
важна
именно
высо
-
та
,
а
не
длина
,
потому
что
длинный
наклонный
столб
давит
на
дно
совершенно
так
же
,
как
и
короткий
Что
тяжелее
?
На
одну
чашку
равноплечих
весов
поставлено
ведро
,
до
краев
наполненное
е
ведро
,
тоже
полное
до
краев
,
но
в
нем
пла
-
вает
кусо
тян
как
ет
?
Я
пробовал
задавать
эту
задачу
разным
лицам
и
получал
разноречивые
ответы
.
Одни
отвечали
,
что
должно
перетянуть
то
ведро
,
в
котором
плавает
дерево
,
потому
что
«
кроме
воды
,
в
ведре
есть
еще
и
дерево
».
Другие
–
что
,
наоборот
,
перетянет
вода
тяжелее
дерева
».
Но
ни
то
,
ни
другое
не
верно
:
оба
ведра
имеют
одинаковый
вес
.
Во
втором
ведре
,
правда
,
воды
меньше
,
нежели
в
первом
,
пото
-
му
что
плавающий
кусок
дерева
вытесняет
некоторый
ее
объем
.
Но
,
но
закону
плавания
,
всякое
плавающее
тело
вытесняет
своей
погруженной
частью
ровно
столько
жидкости
(
по
весу
),
с
Рис
. 53.
Оба
ведра
одинаковы
и
наполнены
ев
;
в
одном
плавает
ку
водой
до
кра
сок
дерева
.
Которое
перетянет
?
это
тело
.
Вот
почему
весы
и
должны
оставаться
в
равновесии
.
Решите
теперь
такую
задачу
.
Я
ставлю
на
одну
чашку
весов
стакан
с
водой
и
рядом
кладу
гирьку
.
Когда
весы
уравновешены
гирями
на
другой
чашке
,
я
роняю
гирьку
По
закону
Архимеда
,
гирька
в
воде
становится
легче
,
чем
была
вне
воды
.
Можно
,
казалось
бы
,
ожидать
,
что
чашка
весов
со
стаканом
поднимется
.
Между
тем
в
действительности
весы
останутся
в
равновесии
.
Как
это
объяснить
?
Гирька
в
стакане
вытеснила
часть
воды
,
которая
оказались
выше
первона
-
чального
уровня
;
вследствие
этого
увеличивается
давление
на
дно
сосуда
,
так
что
дно
испытывает
добавочную
силу
,
равную
потере
веса
гирькой
.
Насколько
легче
стала
гирька
,
настолько
же
тяжелее
стала
вода
в
стакане
;
общий
вес
их
не
изменился
,
и
поэтому
равновесие
чашек
не
нарушается
.
Естественная
форма
жидкости
Мы
привыкли
думать
,
что
жидкости
не
имеют
никакой
собственной
формы
.
Это
неверно
.
Естественная
форма
жидкости
–
шар
.
Обычно
сила
тяжести
мешает
жидкости
принимать
эту
форму
,
и
жидкость
либо
растекается
тонким
слоем
,
если
разлита
без
сосуда
,
либо
же
принимает
форму
сосуда
,
если
налита
в
него
.
Находясь
внутри
другой
жидкости
с
такой
же
плотностью
,
жидкость
,
по
закону
Архимеда
, «
теряет
»
свой
вес
:
она
словно
ничего
не
весит
,
тяжесть
на
нее
не
дей
-
ствует
–
и
тогда
жидкость
принимает
свою
естественную
,
шарообразную
форму
.
Оливковое
масло
плавает
в
воде
,
но
тонет
в
спирте
.
Можно
поэтому
приго
-
товить
такую
смесь
из
воды
и
спирта
,
в
которой
масло
не
тонет
и
не
всплывает
.
Введя
в
эту
смесь
немного
масла
посредством
шприца
,
мы
увидим
странную
вещь
:
масло
собирается
в
большую
круглую
каплю
,
которая
не
всплывает
и
не
тонет
,
а
висит
неподвижно
(
*)
.
Опыт
надо
проделывать
терпеливо
и
осторожно
,
иначе
получится
не
одна
большая
капля
,
а
несколько
шариков
поменьше
.
Но
и
в
таком
виде
опыт
доста
-
точно
интересен
.
Это
,
однако
,
еще
не
все
.
Пропустив
через
центр
масляного
шара
длинный
деревянный
стерженек
(
или
проволоку
),
вращают
его
. (
Опыт
удается
лучше
,
если
насадить
на
ось
небольшой
смоченный
маслом
картонный
кружочек
,
кото
-
рый
весь
оставался
бы
внутри
шара
.)
Под
влиянием
вращения
шар
начинает
сна
-
чала
сплющиваться
,
а
затем
через
несколько
секунд
отделяет
от
себя
кольцо
Разрываясь
на
части
,
кольцо
это
образует
не
бесформенные
куски
,
а
новые
шарообразные
капли
,
которые
продолжают
кружиться
около
центрально
-
Рис
. 54.
Масло
внутри
сосуда
с
разбав
-
ленным
спиртом
собирается
в
шар
,
который
не
тонет
и
не
всплывает
(
опыт
Плато
).
Рис
. 55.
Если
масляный
шар
в
спирте
быстро
вращать
при
помощи
воткнутого
в
него
стерженька
,
от
шара
отделяется
кольцо
.
58
*)
Чтобы
форма
шара
не
казалась
искаженной
,
нужно
производить
опыт
в
сосуде
с
плоскими
стен
-
ками
(
или
в
сосуде
любой
формы
,
но
поставленном
внутри
наполненного
водой
сосуда
с
плоскими
стенками
).