Файл: Практическое задание 2 Расчет цилиндрической передачи.docx

= 1.

Коэффициент 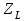, учитывающий влияние смазки, при отсутствии экспе­риментальных данных, принимаем .

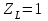Коэффициент 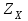, учитывающий размер зубчатого колеса, в общем случае определяется по кривой, приведенной на рис 2.8. При d < 700 мм следует принимать .





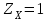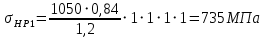
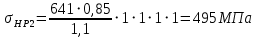
В качестве допускаемого контактного напряжения принимают:

– для косозубых передач

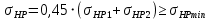, (2.34)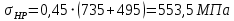



при этом должно выполняться условие:

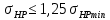
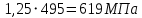
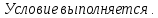
2.4. Расчет на контактную прочность при действии максимальной нагрузки

При действии максимальной нагрузки 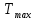наибольшее за заданный срок службы контактное напряжение 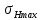не должно превышать допускаемого :

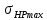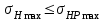. (2.35)

Напряжение 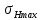определяют по формуле,

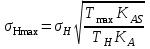, (2.36)

где 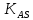– коэффициент внешней динамической нагрузки при расчетах на прочность от максимальной нагрузки (табл. 2.14), .

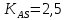Допускаемое контактное напряжение при максимальной нагрузке, не вызывающее остаточных деформаций или хрупкого разрушения поверх­ностного слоя

---

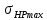
, зависит от способа химико-термической обработки зубчатого колеса и от характера изменения твердости по глубине зуба.

Для зубчатых колес, подвергнутых нормализации, улучшению или объемной закалке с низким отпуском, принимают:

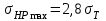; (2.37)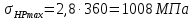





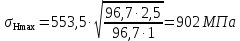
Условие выполняется.

2.5. Расчет зубьев на выносливость при изгибе

А. Определение расчетного изгибного напряжения

Расчетом определяют напряжение в опасном сечении на переходной поверхности зуба для каждого зубчатого колеса.

Расчет необходим для предотвращения усталостного излома зубьев. Устанавливается сопоставлением расчетного напряжения от изгиба в опасном сечении на переходной поверхности и допускаемого напряжения:

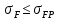. (2.40)

Расчетное напряжение при изгибе определяют по формуле

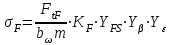, (2.41)

где 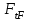– окружная сила на делительном цилиндре, Н;

– рабочая ширина зацепления зубчатой передачи, мм;

m – нормальный модуль, мм;

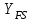– коэффициент, учитывающий форму зуба и концентрацию напряжений;

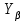– коэффициент, учитывающий влияние наклона зуба;

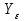– коэффициент, учитывающий перекрытие зубьев;

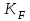– коэффициент нагрузки.

Коэффициент 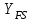, учитывающий форму зуба и концентрацию напряже­ний, определяют по формуле:

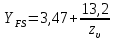(2.43)

где ;

---

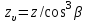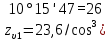
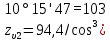
x– коэффициент смещения, мм.





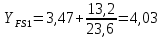
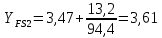
Коэффициент 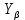, учитывающий влияние угла наклона зубьев, определяется по формуле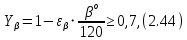



где значение угла подставляется в формулу в градусах;

– коэффициент осевого перекрытия, который определяется по формуле: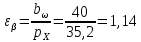



где 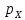– осевой шаг: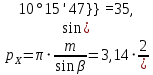



Коэффициент 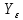, учитывающий перекрытие зубьев, для косозубых передач определяют по формулам: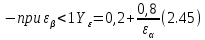







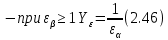
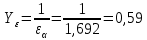
где 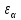– коэффициент торцевого перекрытия.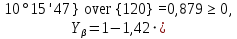



Полученное значение коэффициента должно находиться в пределах:

.

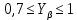Условие выполняется.

Коэффициент нагрузки определяют по формуле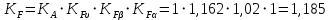

(2.47)

где 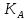– коэффициент, учитывающий внешнюю динамическую нагрузку (не учтенную в циклограмме нагружения), – по табл. 2.8, ;

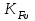– коэффициент, учитывающий динамическую нагрузку, возникающую в зацеплении до зоны резонанса;

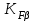– коэффициент, учитывающий неравномерность распределения на­грузки по длине контактных линий;

---

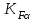– коэффициент, учитывающий распределение нагрузки между зубьями.

Коэффициент , учитывающий динамическую нагрузку, можно определить по формуле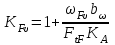

. (2.48)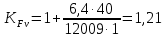



Все величины, входящие в формулу 2.48, найдены ранее, кроме _F – удельной окружной динамической силы (Н/мм), которая может быть найдена по следующей зависимости:

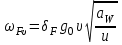, (2.49)

где 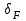– коэффициент, учитывающий влияние вида зубчатой передачи и модификации профиля зубьев (для косозубых и шевронных передач 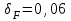; для прямозубых передач с модификацией головки 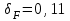; для прямозубых передач без модификации головки );

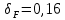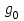– коэффициент, учитывающий влияние разности шагов зацепления зубьев шестерни и колеса, определяется по табл. 2.11 в зависимости от степени точности по нормам плавности и модуля зацепления,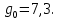



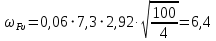
Коэффициент 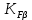, учитывающий неравномерность распределения на­грузки по длине контактных линий, определяется по графику, представленному на рис. 2.9, в зависимости от коэффициента и отношения 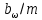. Более точно коэффициент может быть определен по ГОСТ 21354–87,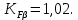

Коэффициент 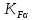, учитывающий неравномерность распределения нагрузки между зубьями

---

, определяется в зависимости от значения :

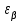(2.50)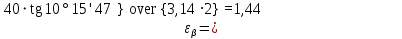



Если условие (2.41) выполняется, то коэффициент 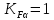; если не выпол­няется, то определяется по следующей формуле: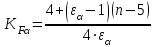

, (2.51)

где n – степень точности по нормам контакта. Если n  9, то принимаем n = 9,

аналогично при n  5, принимаем n = 5;

– коэффициент торцового перекрытия.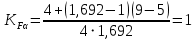

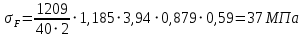
Б. Допускаемые напряжения в проверочном расчете на изгиб

Между допускаемым напряжением 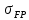и пределом выносливости 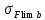существует следующая взаимосвязь:

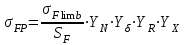, (2.52)

где 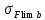– предел выносливости зубьев при изгибе, соответствующий базовому числу циклов напряжений, МПа;

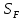– коэффициент запаса прочности;

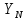– коэффициент долговечности;

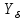– коэффициент, учитывающий градиент напряжения и чувствительность материала к концентрации напряжений;

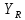– коэффициент, учитывающий шероховатость переходной поверхности (выбираем в зависимости от вида обработки по табл. 2.13);

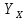– коэффициент, учитывающий размеры зубчатого колеса.

Коэффициент запаса прочности 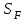определяется в зависимости от способа термической и химико-термической обработки и вероятности неразрушения по таблицам прил. 1.

---