ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 25.10.2023
Просмотров: 282
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
Лекция 1. Введение в радиоэлектронику
Лекция 2. Сигналы и их временные модели
Лекция 3. Сигналы и их спектры
Лекция 4. Дискретизация сигнала и спектра
Лекция 5. Амплитудно-модулированные колебания
Лекция 6. Колебания с угловой и импульсной модуляцией
Примечание. Знак "+" означает возможность применения данного сигнала
Лекция 7. Линейные радиотехнические цепи
), под ним немодулированная высокочастотная несущая uн(t), внизу результирующий амплитудно-модулированный сигнал uАМ(t).
Рассмотрим спектр АМК при модуляции чистым тоном. Раскрыв скобки, преобразуем выражение (5.3) так
uАМ(t) = U0 [1+ Mcos (F0t + 0)] cos(f0t+0) =
= U0cos(f0t+0) + U0Mcos (F0t + 0) cos(f0t+0).
Воспользуемся тригонометрической формулой для произведения косинусов:
uАМ(t) = U0cos(f0t+0) +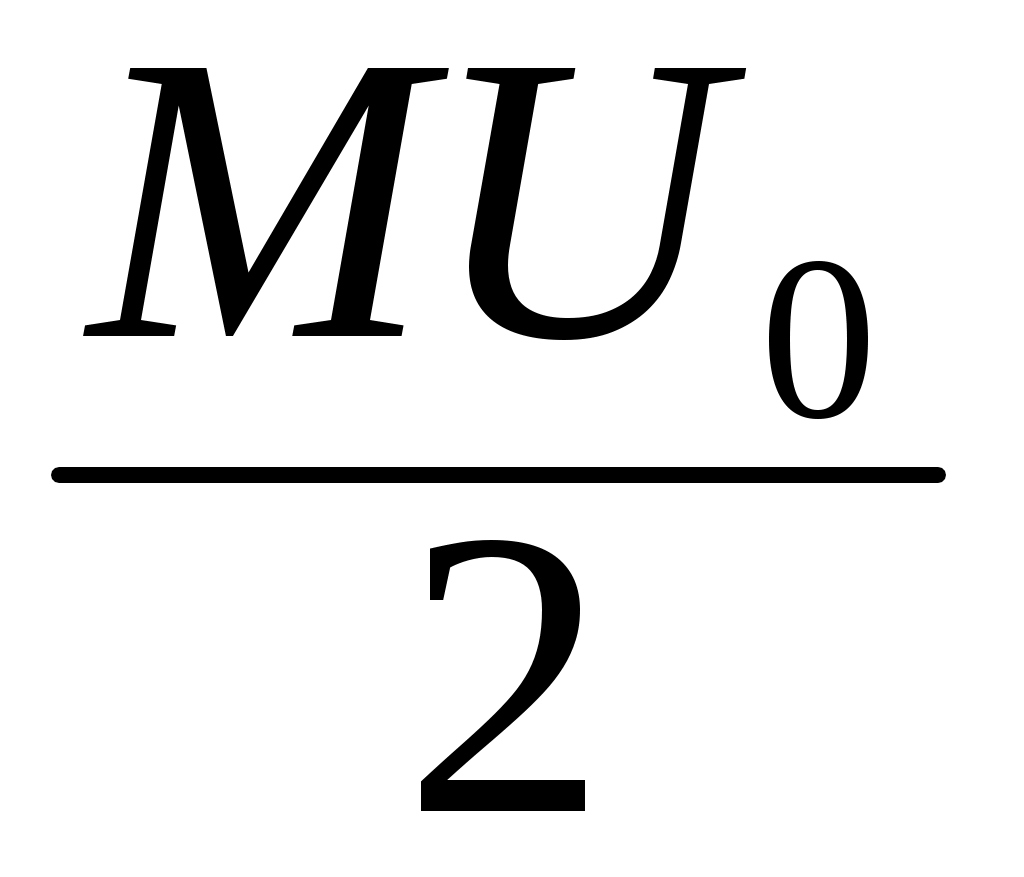
cos [(f0 +F0)t + 0 + 0] +
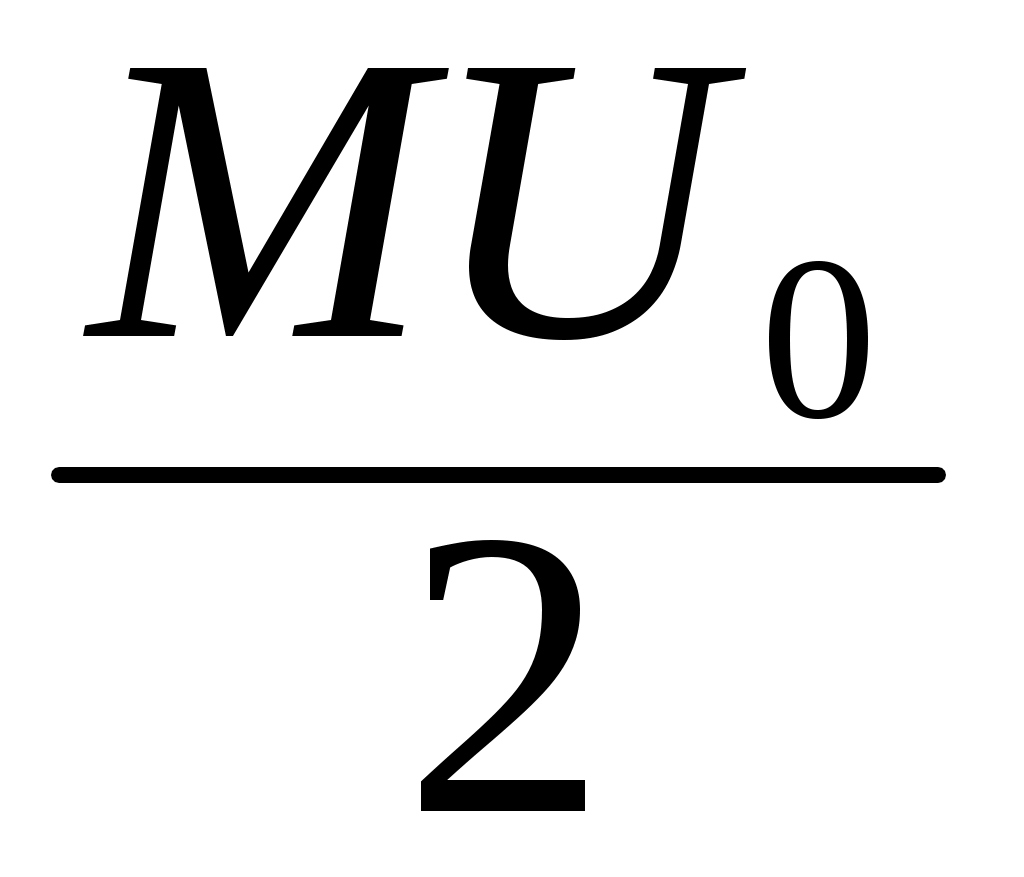+ cos [(f0 –F0)t + 0 – 0]. (5.4)
Рассмотрим подробнее каждое слагаемое выражения (5.4).
Очевидно, что первое слагаемое соответствует немодулированной несущей с амплитудой U0 , частотой f0 и начальной фазой 0. Второе слагаемое – гармонический сигнал с амплитудой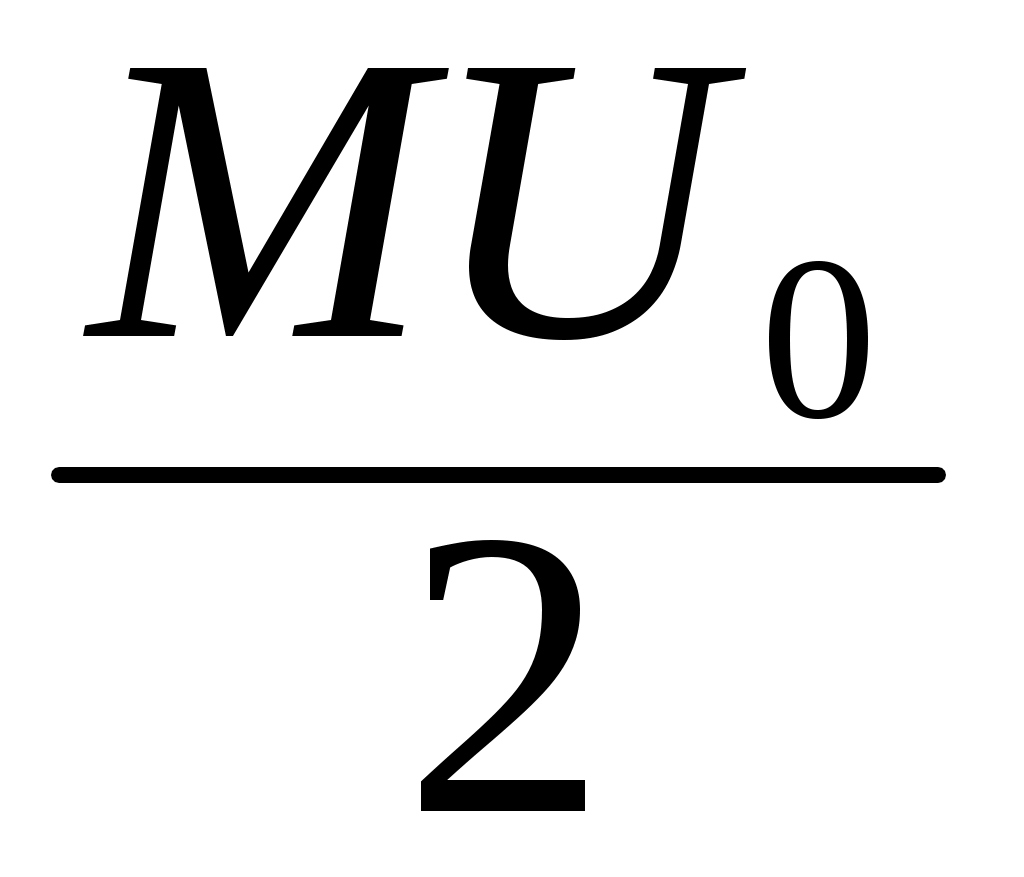 , частотой f0 +F0 и начальной фазой 0 + 0. Это верхнее боковое колебание (ВБК). Наконец, третье слагаемое представляет собой гармонический сигнал с амплитудой 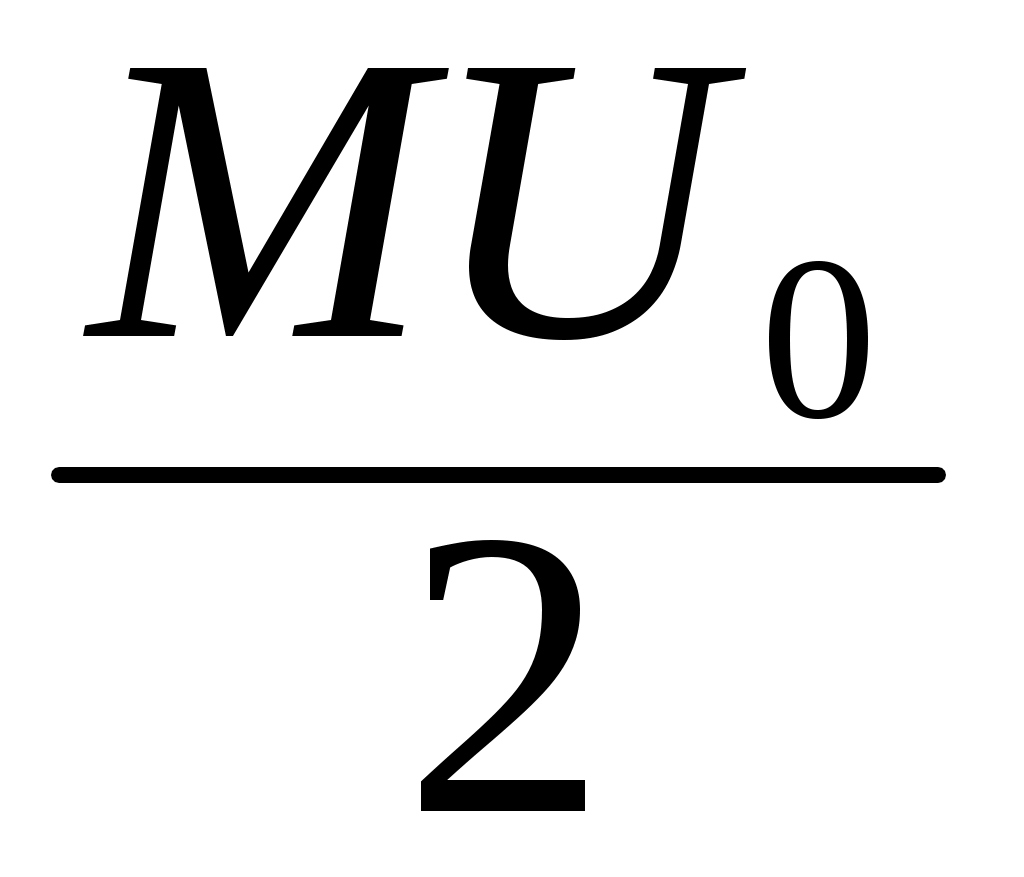, частотой f0 – F0 и начальной фазой 0 – 0 и носит название нижнего бокового колебания (НБК).
На частотной оси сигналу вида (5.4) соответствует спектр из трех компонентов, изображенный на рис. 5.2.
Примечание. Соотношения амплитуд и фаз на рис. 5.2 носят качественный характер.
Из рис. 5.2 очевидно, что амплитуды верхнего и нижнего боковых колебаний равны между собой и меньше, чем амплитуда несущей (поскольку М1). Спектр амплитуд симметричен относительно вертикальной оси, проходящей через точку с частотой f0.
Таким образом, в процессе амплитудной модуляции осуществляется перенос НЧ спектральной составляющей с частотой F0, в область частот в окрестности
f0, причем F0 << f0.
Отметим, что ширина спектра амплитудно-модулированного колебания оказывается равной удвоенной частоте модулирующего сигнала:
fАМ = 2F0. (5.5)
Рассмотрим более сложный случай модуляции произвольным сигналом.
Из лекции 3 известно, что произвольный сигнал можно представить в виде суммы гармоник:
U(t) =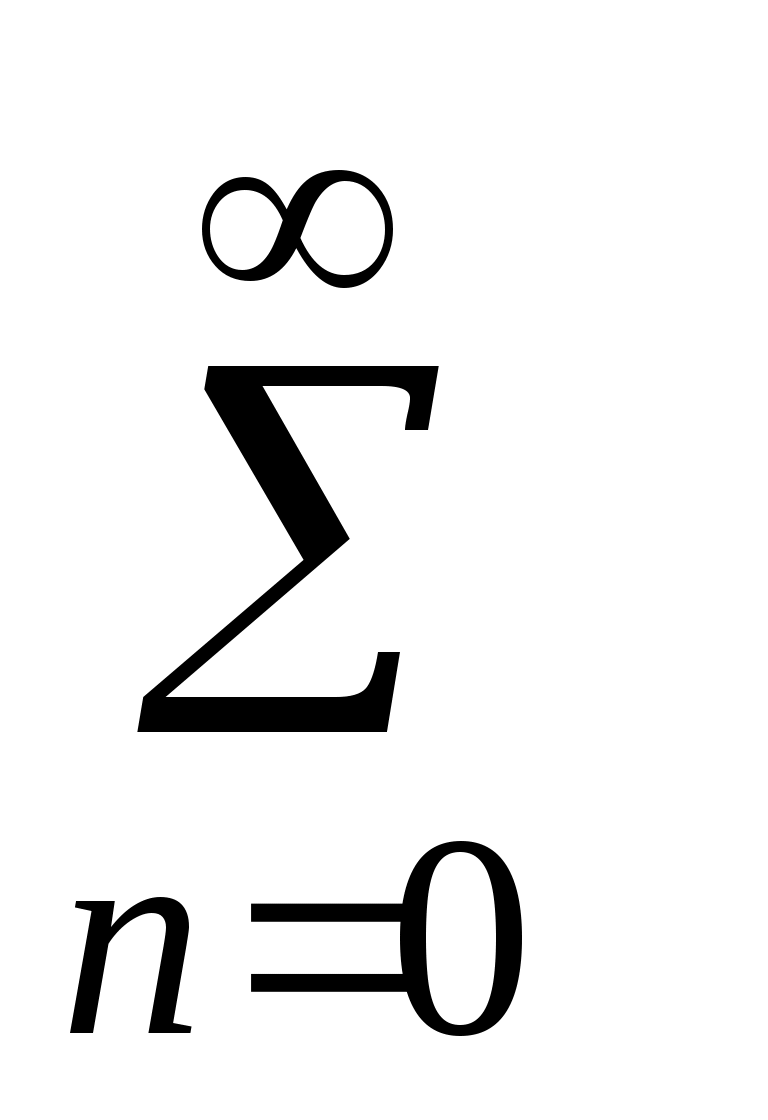
[Uncos(2nF0t) + 0]. (5.6)
Примем для упрощения, что 0 = 0 = 0, и ограничимся рассмотрением спектра амплитуд. Пусть постоянная составляющая в модулирующем сигнале отсутствует.
С учетом этого, подстановка (5.6) в (5.4) даст следующий результат:
uАМ(t) = U0cos(f0t+0) +
+
{
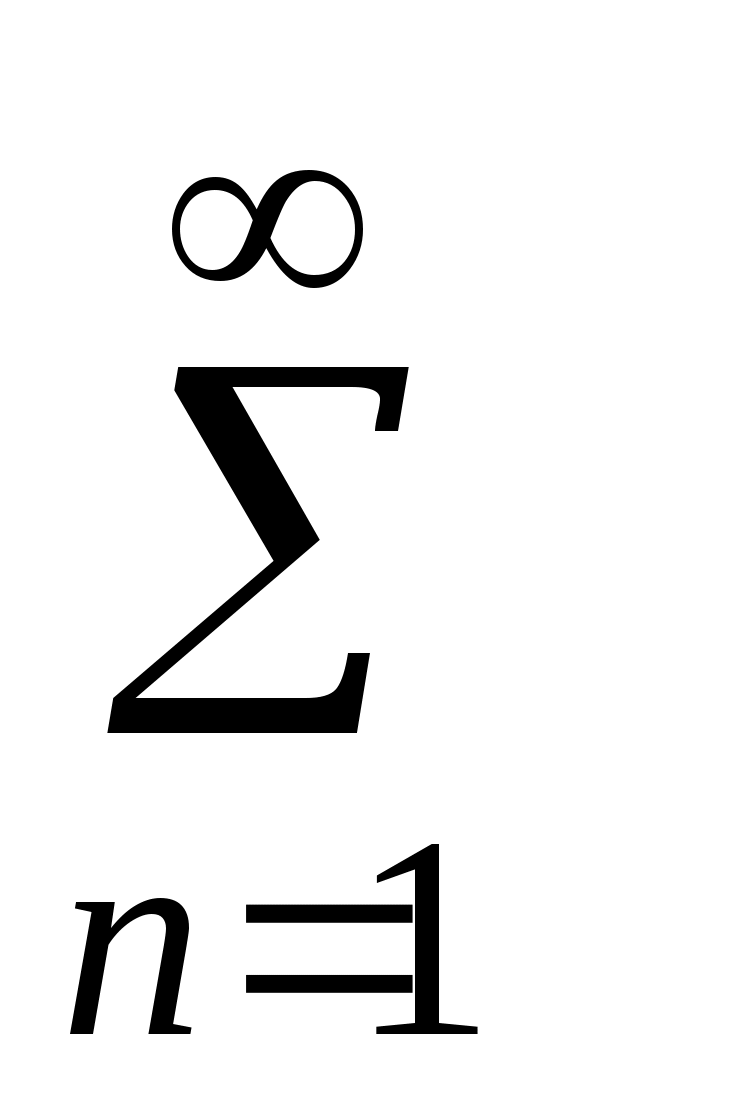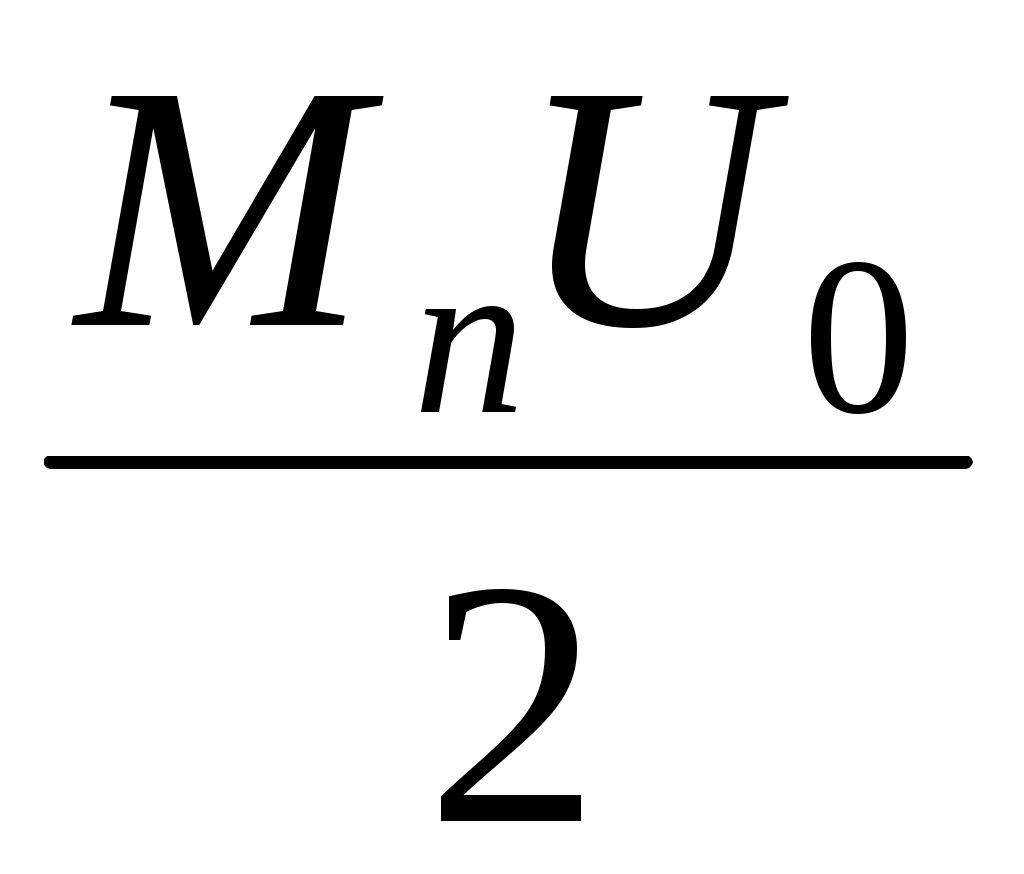cos [(f0 +Fn)t ] + 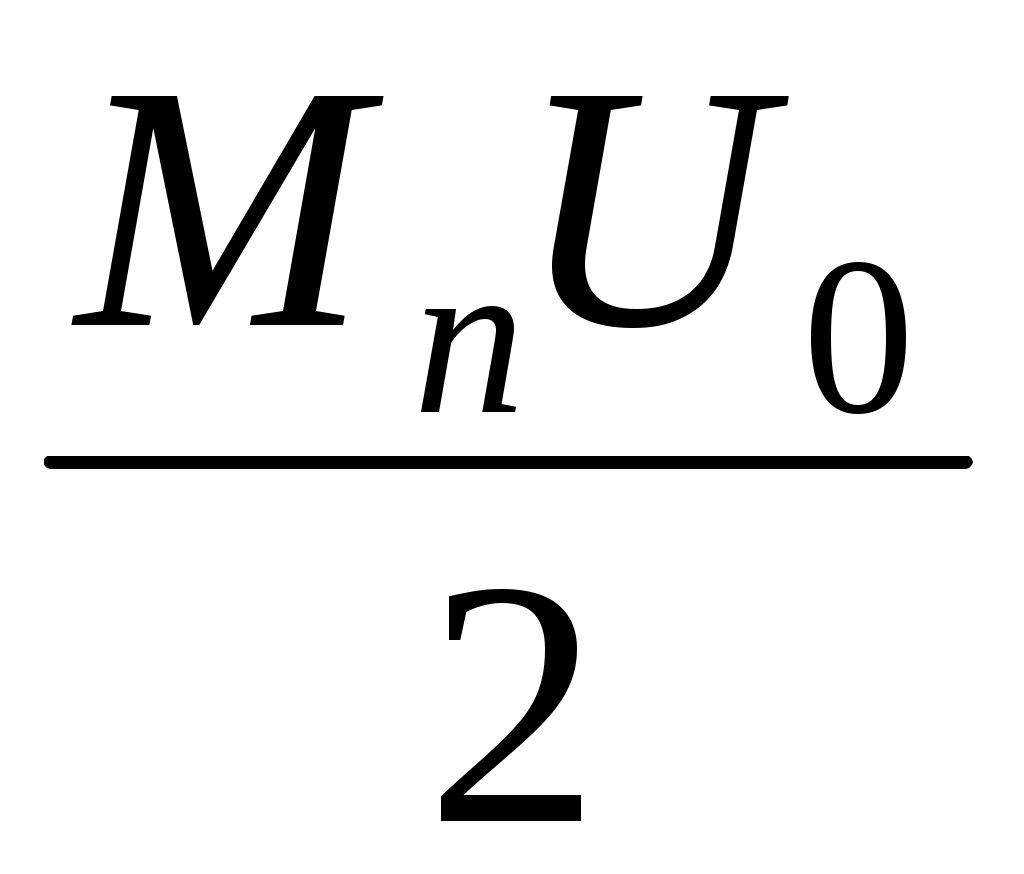cos [(f0 –Fn)t ]}, (5.7)
где Mn = Un /U0 парциальные коэффициенты модуляции, Fn – частоты исходных спектральных составляющих модулирующего сигнала.
Воспользуемся также сформулированным ранее правилом, что для физически реализуемого сигнала с ростом частоты амплитуда спектральных составляющих, как правило, убывает. Следовательно, с ростом n Mn будет уменьшаться. Рисунок 5.3 качественно иллюстрирует исходную и результирующую спектральные диаграммы.
Таким образом, при модуляции структура спектра модулирующего НЧ-сигнала полностью сохраняется, а ширина спектра результирующего АМК равна 2Fmax, где Fmax – максимальная частота в спектре исходного НЧ сигнала.
При рассмотрении АМК сигнал удобно представить на комплексной плоскости в виде векторной диаграммы (рис. 5.4). Длина вектора соответствует амплитуде, а его угловое положение – фазе. Вращение вектора с некоторой угловой скоростью = 2f имитируется поворотом самой координатной системы и соответствует изменению времени t.
На рис. 5.5 представлена векторная диаграмма АМК при модуляции чистым тоном.
Рис. 5.5
Вектор несущей отложен из точки 0, он имеет амплитуду U0 и начальную фазу 0. Векторы боковых колебаний отложены из точки 0'. В результате сложения векторов получается результирующий вектор U. С течением времени происходит вращение векторов боковых колебаний с угловой скоростью 0 = 2F0. Сама координатная система поворачивается вокруг точки 0 с угловой скоростью 0 = 2f0.
Поскольку амплитуды (UНБК , UВБК), фазы 0 и угловые скорости 0 ВБК и НБК равны, то в процессе модуляции с течением времени изменяется длина результирующего вектора U , а его угловое положение остается неизменным, т.е. 0 = const.
Рассмотрим теперь энергетические характеристики АМК.
АМК представляет собой периодический процесс, следовательно, основной энергетической характеристикой служит средняя мощность, определяемая по формуле (2.3), интегрирование в которой осуществляется в течение интервала, равного периоду.
Из выражения (5.3) очевидно, что существует два существенно различных периода:
1) период огибающей TF = 1/F0 ;
2) период несущей Tf = 1/f0.
Определим сначала среднюю мощность АМК за период несущей.
Так как Tf << TF, то на протяжении интервала времени, равного периоду несущей, изменениями амплитуды можно пренебречь и считать U(t) = const.
Возможны три основных случая:
1. cos (F0t + 0) = 0; U(t) =0; uАМ(t) = U0cos(f0t+0), тогда
Pср = 1/ Tf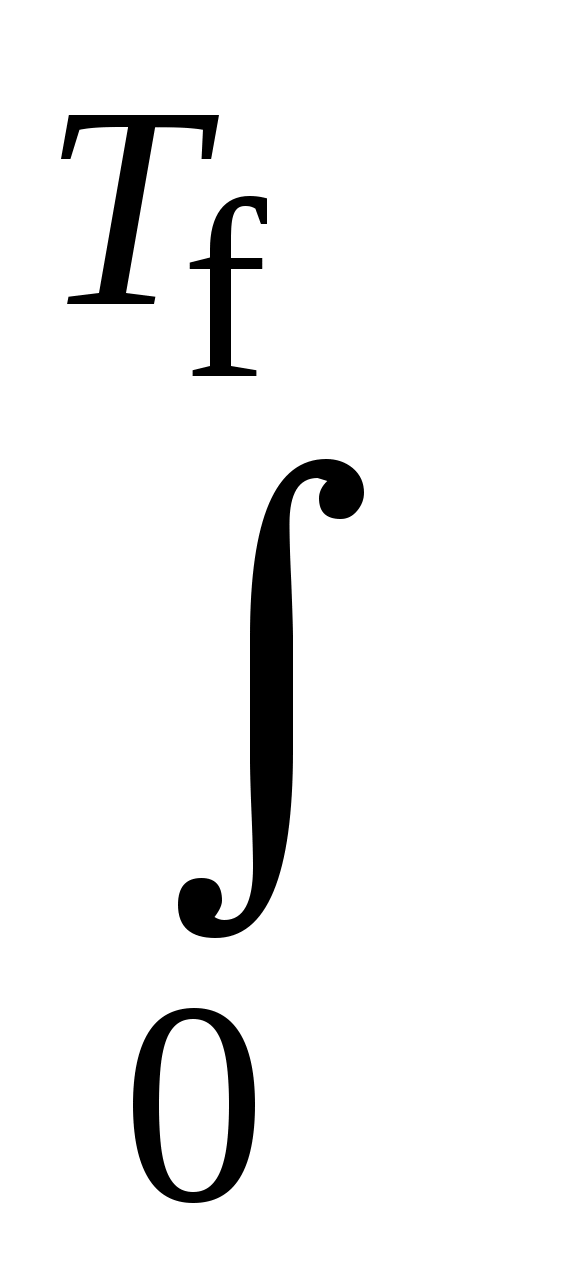
U02cos2(f0t+0) dt = U02/2 = P0. (5.8)
2. cos (F0t + 0) = 1; U(t) = Umax ; uАМ(t) = U0 (1+M)cos(f0t+0), тогда
Pср = Pmax = U02/2 (1+M)2 = P0(1+M)2 . (5.9)
3. cos (F0t + 0) = –1; U(t) = Umin ; uАМ(t) = U0 (1–M)cos(f0t+0), тогда
Pср = Pmin = U02/2 (1–M)2 = P0(1–M)2 . (5.10)
Пример 5.1.
Пусть M = 1. Рассчитать Pmax и Pmin.
Решение.
Подставив коэффициент модуляции в формулы (5.9) и (5.10), получим
Pmin = 0; Pmax = 4P0 , т.е. мощность АМК с течением времени значительно меняется, поэтому во всем динамическом диапазоне мощностей необходимо обеспечить неискаженную передачу сигнала.
Теперь найдем среднюю мощность за период огибающей.
Допущение о постоянстве амплитуды на этом временном интервале не справедливо, поэтому представим формулу (5.4) в следующем виде:
uАМ(t) = uн(t) + uнбк(t) + uвбк(t),
где
uн(t) = U0cos(f0t+0);
uнбк(t) =
cos [(f0 –F0)t + 0 – 0];
uвбк(t) = cos [(f0 +F0)t + 0 + 0].
При интегрировании по формуле (2.3) учтем, что несущая и боковые ортогональны, в результате окончательно получим:
Pср = Р0 + Рнбк + Рвбк = U02/2 + 1/2(МU02/2)2 + 1/2(МU02/2)2 = Р0(1+М2/2). (5.11)
Аналогичный результат можно получить, воспользовавшись спектральным представлением АМК и теоремой Парсеваля.
Заметим, что формула (5.11) дает возможность определить полную мощность АМК, а полезная мощность в выражении (5.11) равна сумме мощностей боковых колебаний
Рп = Рнбк + Рвбк.
Пример 5.2.
Пусть M=0,5. Определить, какую долю общей мощности составляет полезная мощность АМК.
Решение.
Из формулы (5.11) получаем
Рп = Р0М2/2 = 0,125 Р0.
Полезная мощность мала по сравнению с общей затрачиваемой мощностью, для улучшения энергетических характеристик используют разновидности АМК: балансную и однополосную модуляцию.
Идея балансной амплитудной модуляции (БАМ или DSB) заключается в изменении фазы несущей за половину периода огибающей. В результате за полный период огибающей несущая компенсируется и сигнал БАМ при модуляции чистым тоном описывается следующим выражением:
uБАМ(t) = cos [(f0 –F0)t + 0 – 0
] + cos [(f0 +F0)t + 0 + 0].
Идеальная спектральная диаграмма БАМ при модуляции произвольным сигналом изображена на рис. 5.6.
Как видим, в идеальном случае спектральная составляющая несущей отсутствует, на практике на частоте несущей f0 передают относительно небольшой по уровню пилот-сигнал для улучшения демодуляции на приемной стороне.
В результате энергетические характеристики по сравнению с классической АМ улучшаются, а ширина спектра остается неизменной.
Дальнейшим улучшением АМ является однополосная модуляция (ОБП или SSB).
При ОБП на частоте несущей передают небольшой по уровню пилот-сигнал, а из информационных составляющих оставляют только верхнюю (или нижнюю) боковые полосы. В результате доля полезной мощности возрастает, а ширина спектра по сравнению с обычной АМ и БАМ уменьшается в 2 раза.
Однополосная и балансная модуляция особенно целесообразны в условиях ограниченности частотного диапазона: для профессиональной и любительской радиосвязи, а также при передаче широкополосных сигналов, например сигнала изображения в телевидении.
Особая разновидность амплитудной модуляции – полярная модуляция.
Сигналы с полярной модуляцией были предложены для организации стереофонического радиовещания еще в 60-е гг. ХХ века.
Суть метода иллюстрирует рис. 5.7.
Предположим, что в правом и левом канале передаются гармонические сигналы с частотами, различающимися в 2 раза (Uпк и Uлк на рис. 5.7 вверху).
Эти сигналы модулируют ВЧ поднесущую uпн так, что в результате получается несимметричный сигнал (uПМ на рис. 5.7 внизу).
В СССР была принята система с полярно-модулированным (ПМ) сигналом (стандарт Международной организации радиовещания и телевидения OIRT). При этом частота поднесущей равна fпн = 31,25 кГц , а ее уровень подавляется на 14 дБ. В принятом практически во всем мире стандарте международного консультативного комитета по радиовещанию (CCIR), разработанном в США, при формировании стереосигнала поднесущая 38 кГц подавляется полностью, а для ее восстановления в приемнике передается пилот-тон на частоте fпн/2 = 38/2 =19 кГц.
Схематично спектры сигналов OIRT и CCIR изображены на рис. 5.8.
Рассмотрим спектр АМК при модуляции чистым тоном. Раскрыв скобки, преобразуем выражение (5.3) так
uАМ(t) = U0 [1+ Mcos (F0t + 0)] cos(f0t+0) =
= U0cos(f0t+0) + U0Mcos (F0t + 0) cos(f0t+0).
Воспользуемся тригонометрической формулой для произведения косинусов:
uАМ(t) = U0cos(f0t+0) +
cos [(f0 +F0)t + 0 + 0] + +
cos [(f0 –F0)t + 0 – 0]. (5.4)Рассмотрим подробнее каждое слагаемое выражения (5.4).
Очевидно, что первое слагаемое соответствует немодулированной несущей с амплитудой U0 , частотой f0 и начальной фазой 0. Второе слагаемое – гармонический сигнал с амплитудой
, частотой f0 +F0 и начальной фазой 0 + 0. Это верхнее боковое колебание (ВБК). Наконец, третье слагаемое представляет собой гармонический сигнал с амплитудой , частотой f0 – F0 и начальной фазой 0 – 0 и носит название нижнего бокового колебания (НБК). На частотной оси сигналу вида (5.4) соответствует спектр из трех компонентов, изображенный на рис. 5.2.
Примечание. Соотношения амплитуд и фаз на рис. 5.2 носят качественный характер.
Из рис. 5.2 очевидно, что амплитуды верхнего и нижнего боковых колебаний равны между собой и меньше, чем амплитуда несущей (поскольку М1). Спектр амплитуд симметричен относительно вертикальной оси, проходящей через точку с частотой f0.
Таким образом, в процессе амплитудной модуляции осуществляется перенос НЧ спектральной составляющей с частотой F0, в область частот в окрестности
f0, причем F0 << f0.
Отметим, что ширина спектра амплитудно-модулированного колебания оказывается равной удвоенной частоте модулирующего сигнала:
fАМ = 2F0. (5.5)
Рассмотрим более сложный случай модуляции произвольным сигналом.
Из лекции 3 известно, что произвольный сигнал можно представить в виде суммы гармоник:
U(t) =
[Uncos(2nF0t) + 0]. (5.6)Примем для упрощения, что 0 = 0 = 0, и ограничимся рассмотрением спектра амплитуд. Пусть постоянная составляющая в модулирующем сигнале отсутствует.
С учетом этого, подстановка (5.6) в (5.4) даст следующий результат:
uАМ(t) = U0cos(f0t+0) +
+
{ cos [(f0 +Fn)t ] + cos [(f0 –Fn)t ]}, (5.7)где Mn = Un /U0 парциальные коэффициенты модуляции, Fn – частоты исходных спектральных составляющих модулирующего сигнала.
Воспользуемся также сформулированным ранее правилом, что для физически реализуемого сигнала с ростом частоты амплитуда спектральных составляющих, как правило, убывает. Следовательно, с ростом n Mn будет уменьшаться. Рисунок 5.3 качественно иллюстрирует исходную и результирующую спектральные диаграммы.
Таким образом, при модуляции структура спектра модулирующего НЧ-сигнала полностью сохраняется, а ширина спектра результирующего АМК равна 2Fmax, где Fmax – максимальная частота в спектре исходного НЧ сигнала.
При рассмотрении АМК сигнал удобно представить на комплексной плоскости в виде векторной диаграммы (рис. 5.4). Длина вектора соответствует амплитуде, а его угловое положение – фазе. Вращение вектора с некоторой угловой скоростью = 2f имитируется поворотом самой координатной системы и соответствует изменению времени t.
На рис. 5.5 представлена векторная диаграмма АМК при модуляции чистым тоном.
Рис. 5.5
Вектор несущей отложен из точки 0, он имеет амплитуду U0 и начальную фазу 0. Векторы боковых колебаний отложены из точки 0'. В результате сложения векторов получается результирующий вектор U. С течением времени происходит вращение векторов боковых колебаний с угловой скоростью 0 = 2F0. Сама координатная система поворачивается вокруг точки 0 с угловой скоростью 0 = 2f0.
Поскольку амплитуды (UНБК , UВБК), фазы 0 и угловые скорости 0 ВБК и НБК равны, то в процессе модуляции с течением времени изменяется длина результирующего вектора U , а его угловое положение остается неизменным, т.е. 0 = const.
Рассмотрим теперь энергетические характеристики АМК.
АМК представляет собой периодический процесс, следовательно, основной энергетической характеристикой служит средняя мощность, определяемая по формуле (2.3), интегрирование в которой осуществляется в течение интервала, равного периоду.
Из выражения (5.3) очевидно, что существует два существенно различных периода:
1) период огибающей TF = 1/F0 ;
2) период несущей Tf = 1/f0.
Определим сначала среднюю мощность АМК за период несущей.
Так как Tf << TF, то на протяжении интервала времени, равного периоду несущей, изменениями амплитуды можно пренебречь и считать U(t) = const.
Возможны три основных случая:
1. cos (F0t + 0) = 0; U(t) =0; uАМ(t) = U0cos(f0t+0), тогда
Pср = 1/ Tf
U02cos2(f0t+0) dt = U02/2 = P0. (5.8)2. cos (F0t + 0) = 1; U(t) = Umax ; uАМ(t) = U0 (1+M)cos(f0t+0), тогда
Pср = Pmax = U02/2 (1+M)2 = P0(1+M)2 . (5.9)
3. cos (F0t + 0) = –1; U(t) = Umin ; uАМ(t) = U0 (1–M)cos(f0t+0), тогда
Pср = Pmin = U02/2 (1–M)2 = P0(1–M)2 . (5.10)
Пример 5.1.
Пусть M = 1. Рассчитать Pmax и Pmin.
Решение.
Подставив коэффициент модуляции в формулы (5.9) и (5.10), получим
Pmin = 0; Pmax = 4P0 , т.е. мощность АМК с течением времени значительно меняется, поэтому во всем динамическом диапазоне мощностей необходимо обеспечить неискаженную передачу сигнала.
Теперь найдем среднюю мощность за период огибающей.
Допущение о постоянстве амплитуды на этом временном интервале не справедливо, поэтому представим формулу (5.4) в следующем виде:
uАМ(t) = uн(t) + uнбк(t) + uвбк(t),
где
uн(t) = U0cos(f0t+0);
uнбк(t) =
cos [(f0 –F0)t + 0 – 0]; uвбк(t) =
cos [(f0 +F0)t + 0 + 0]. При интегрировании по формуле (2.3) учтем, что несущая и боковые ортогональны, в результате окончательно получим:
Pср = Р0 + Рнбк + Рвбк = U02/2 + 1/2(МU02/2)2 + 1/2(МU02/2)2 = Р0(1+М2/2). (5.11)
Аналогичный результат можно получить, воспользовавшись спектральным представлением АМК и теоремой Парсеваля.
Заметим, что формула (5.11) дает возможность определить полную мощность АМК, а полезная мощность в выражении (5.11) равна сумме мощностей боковых колебаний
Рп = Рнбк + Рвбк.
Пример 5.2.
Пусть M=0,5. Определить, какую долю общей мощности составляет полезная мощность АМК.
Решение.
Из формулы (5.11) получаем
Рп = Р0М2/2 = 0,125 Р0.
Полезная мощность мала по сравнению с общей затрачиваемой мощностью, для улучшения энергетических характеристик используют разновидности АМК: балансную и однополосную модуляцию.
Идея балансной амплитудной модуляции (БАМ или DSB) заключается в изменении фазы несущей за половину периода огибающей. В результате за полный период огибающей несущая компенсируется и сигнал БАМ при модуляции чистым тоном описывается следующим выражением:
uБАМ(t) =
cos [(f0 –F0)t + 0 – 0
] +
cos [(f0 +F0)t + 0 + 0]. Идеальная спектральная диаграмма БАМ при модуляции произвольным сигналом изображена на рис. 5.6.
Как видим, в идеальном случае спектральная составляющая несущей отсутствует, на практике на частоте несущей f0 передают относительно небольшой по уровню пилот-сигнал для улучшения демодуляции на приемной стороне.
В результате энергетические характеристики по сравнению с классической АМ улучшаются, а ширина спектра остается неизменной.
Дальнейшим улучшением АМ является однополосная модуляция (ОБП или SSB).
При ОБП на частоте несущей передают небольшой по уровню пилот-сигнал, а из информационных составляющих оставляют только верхнюю (или нижнюю) боковые полосы. В результате доля полезной мощности возрастает, а ширина спектра по сравнению с обычной АМ и БАМ уменьшается в 2 раза.
Однополосная и балансная модуляция особенно целесообразны в условиях ограниченности частотного диапазона: для профессиональной и любительской радиосвязи, а также при передаче широкополосных сигналов, например сигнала изображения в телевидении.
Особая разновидность амплитудной модуляции – полярная модуляция.
Сигналы с полярной модуляцией были предложены для организации стереофонического радиовещания еще в 60-е гг. ХХ века.
Суть метода иллюстрирует рис. 5.7.
Предположим, что в правом и левом канале передаются гармонические сигналы с частотами, различающимися в 2 раза (Uпк и Uлк на рис. 5.7 вверху).
Эти сигналы модулируют ВЧ поднесущую uпн так, что в результате получается несимметричный сигнал (uПМ на рис. 5.7 внизу).
В СССР была принята система с полярно-модулированным (ПМ) сигналом (стандарт Международной организации радиовещания и телевидения OIRT). При этом частота поднесущей равна fпн = 31,25 кГц , а ее уровень подавляется на 14 дБ. В принятом практически во всем мире стандарте международного консультативного комитета по радиовещанию (CCIR), разработанном в США, при формировании стереосигнала поднесущая 38 кГц подавляется полностью, а для ее восстановления в приемнике передается пилот-тон на частоте fпн/2 = 38/2 =19 кГц.
Схематично спектры сигналов OIRT и CCIR изображены на рис. 5.8.