Файл: Методические указания и контрольные задания для студентов заочников.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 25.10.2023
Просмотров: 133
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
- N1=0; N1= F1= 18 кН.
Напряжение на первом участке
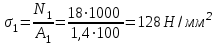
Поскольку ни сила, ни площадь на протяжение всего участка не меняются, то и напряжение по всей длине участка постоянно. На графике – эпюре (рис. 14) это изобразится прямой l (на этом участке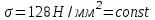 ).
).
Удлинение первого участка
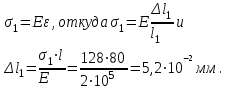
 3. Определяем силу N2 сопротивления второго участка и напряжение
3. Определяем силу N2 сопротивления второго участка и напряжение 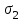 . Правая от второго сечения часть подвергается действию сил F1; F2;и N2;
. Правая от второго сечения часть подвергается действию сил F1; F2;и N2;
F1+F2-N2=0. N2=F1+F2=18+6=24кН
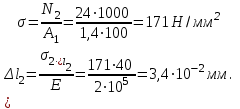
4.Сила N3, напряжение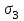 , удлинение l3 третьего участка. Правая от сечения часть балки подвергается действию сил F1; F2; N3.
, удлинение l3 третьего участка. Правая от сечения часть балки подвергается действию сил F1; F2; N3.
F1+F2-N3=0; N3=24кН.
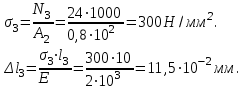
Нанося характерные точки на график, и соединяя их прямыми линиями, получая эпюру напряжений, рис.14.
5.Общее удлинение бруса
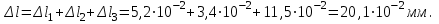
6.Анализируем эпюру. Первый участок прочен.
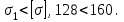
Второй недостаточно прочен, третий не прочен.
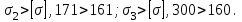
Наиболее нагружен третий участок: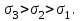
Примечание. Участок 1 находится в стадии упругости. Участок 2 – тоже: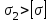 , но незначительно. Допускаемые напряжения назначаются несколько ниже стадии упругости. Поэтому формула закона Гука здесь правомерна.
, но незначительно. Допускаемые напряжения назначаются несколько ниже стадии упругости. Поэтому формула закона Гука здесь правомерна.
На третьем участке напряжения значительно превышают допустимые, что означает переход в стадию текучести. В стадии деформация определяется эксперементально. Формула же применения для демонстрации способа определения полной деформации бруса. На третьем участке может произойти разрушение.
Задание 5.
Проверить прочность, найти наиболее напряженный участок двухступенчатого бруса, напряженного силами F1, F2, если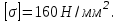 Найти удлинение бруса. Данные своего вариантов взять из таблицы 2.1.
Найти удлинение бруса. Данные своего вариантов взять из таблицы 2.1.
1 2 3 4 5
6 7 8 9 10
Методические указания к выполнению задания 6.
Вращающиеся детали (чаще всего это валы) испытывают деформацию – кручение: касательное относительное вращение поперечных сечений. Противодействие сечений вала кручению определяется крутящим моментом Мк и касательным напряжением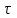 .
.
Чтобы вал упруго сопротивлялся кручению, крутящий момент сечения должен уравновесить вращающие моменты справа или слева от сечения(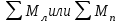 ), то есть
), то есть
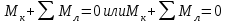
Результат будет одинаков, ибо левая и правая части действуют равным образом друг на друга по принципу равенства действия и противодействия.
Однако крутящий момент недостаточно характеризует сопротивление вала кручению. Очевидно вал меньшего диаметра с тем же крутящим моментом имеет меньшее сопротивление. Поэтому для достаточной оценки сопротивляемости вала кручению применяют другой параметр – касательное напряжение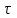 . Касательное напряжение учитывает величины: крутящего момента Мк, диаметр вала d, площадь сечения (круга)
. Касательное напряжение учитывает величины: крутящего момента Мк, диаметр вала d, площадь сечения (круга)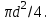
Формула касательного напряжения
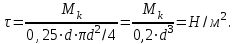
Рабочие напряжения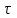 , возникающие в сечении вала при кручении, не должны превышать допустимые
, возникающие в сечении вала при кручении, не должны превышать допустимые 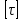 для данного материала. Условие прочности выражается зависимостью
для данного материала. Условие прочности выражается зависимостью
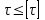 .
.
Для установления наиболее нагруженного участка ступенчатого вала строят эпюру касательных напряжений.
Пример 6. Определить из условия прочности диаметр стального вала постоянного сечения, нагруженного вращающими моментами М1, М2, М3, М4, (рис. 16) при угловой скорости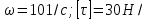 мм2
мм2
, мощности Р1=90 кВт, Р2=60кВт, Р4=30кВт.
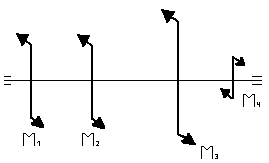 рис.16
рис.16
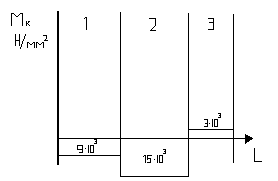 рис.17
рис.17
Решение
1.Разбиваем вал на три участка – по сечениям, в которых приложены вращающие моменты.
2.Находим вращающие моменты
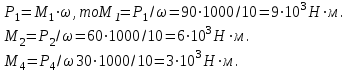
Равномерное вращение обеспечивается условием
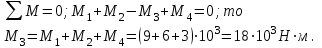
3.В любом сечении участка 1 в условиях прочности должен быть крутящий момент Мк1, уравновешивающий внешние справа (или слева) от сечения.
Справа –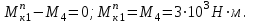
Слева -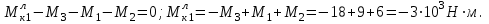
Крутящие моменты равны, поэтому можно строить эпюру и справа и слева. Разные знаки крутящих моментов потому, что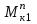 - это момент сопротивления левой части вала кручению правой, а
- это момент сопротивления левой части вала кручению правой, а 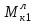 - момент сопротивления правой стороны кручению левой.
- момент сопротивления правой стороны кручению левой.
Естественно они равны и противоположно направлены. Крутящий момент на втором участке
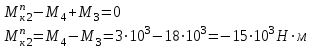
На третьем участке
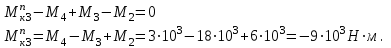
4.Строим эпюру. На всех участках крутящий момент есть постоянная функция – он не зависит от длины вала.
Следовательно, эпюра – прямая параллельная оси l – на первом участке(рис. 17) её координата Мк=3 103Н
103Н м, на втором Мк=-15
м, на втором Мк=-15 103Н
103Н м, на третьемМк=-9
м, на третьемМк=-9 103Н
103Н м.
м.
5.Определяем диаметр вала для наиболее напряжённого второго участка.
Напряжение на первом участке
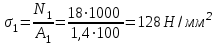
Поскольку ни сила, ни площадь на протяжение всего участка не меняются, то и напряжение по всей длине участка постоянно. На графике – эпюре (рис. 14) это изобразится прямой l (на этом участке
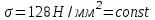 ).
).Удлинение первого участка
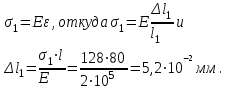
 3. Определяем силу N2 сопротивления второго участка и напряжение
3. Определяем силу N2 сопротивления второго участка и напряжение 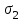 . Правая от второго сечения часть подвергается действию сил F1; F2;и N2;
. Правая от второго сечения часть подвергается действию сил F1; F2;и N2;F1+F2-N2=0. N2=F1+F2=18+6=24кН
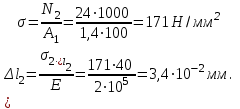
4.Сила N3, напряжение
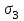 , удлинение l3 третьего участка. Правая от сечения часть балки подвергается действию сил F1; F2; N3.
, удлинение l3 третьего участка. Правая от сечения часть балки подвергается действию сил F1; F2; N3.F1+F2-N3=0; N3=24кН.
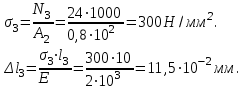
Нанося характерные точки на график, и соединяя их прямыми линиями, получая эпюру напряжений, рис.14.
5.Общее удлинение бруса
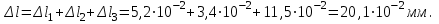
6.Анализируем эпюру. Первый участок прочен.
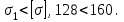
Второй недостаточно прочен, третий не прочен.
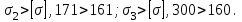
Наиболее нагружен третий участок:
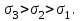
Примечание. Участок 1 находится в стадии упругости. Участок 2 – тоже:
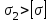 , но незначительно. Допускаемые напряжения назначаются несколько ниже стадии упругости. Поэтому формула закона Гука здесь правомерна.
, но незначительно. Допускаемые напряжения назначаются несколько ниже стадии упругости. Поэтому формула закона Гука здесь правомерна.На третьем участке напряжения значительно превышают допустимые, что означает переход в стадию текучести. В стадии деформация определяется эксперементально. Формула же применения для демонстрации способа определения полной деформации бруса. На третьем участке может произойти разрушение.
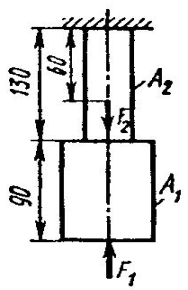
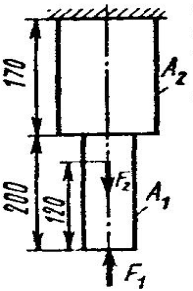
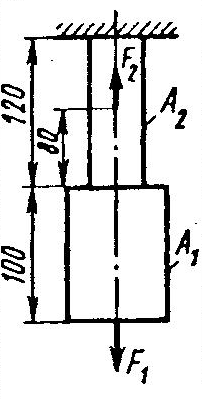
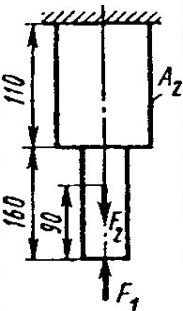
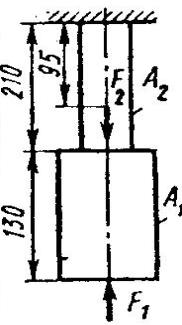
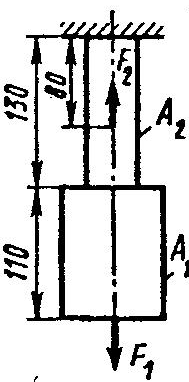
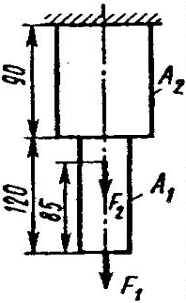
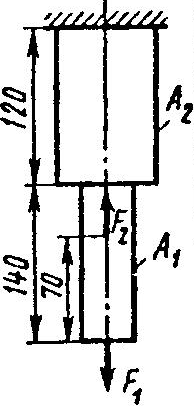
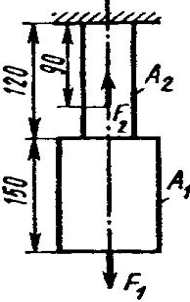
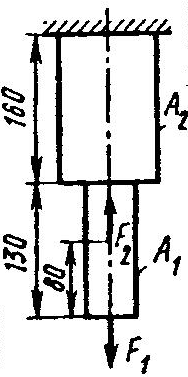
Задание 5.
Проверить прочность, найти наиболее напряженный участок двухступенчатого бруса, напряженного силами F1, F2, если
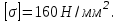 Найти удлинение бруса. Данные своего вариантов взять из таблицы 2.1.
Найти удлинение бруса. Данные своего вариантов взять из таблицы 2.1.| №задачи и схемы на рис.15 | Варианты | F1,кН | F2,кН | А1 см2 | А2,см2 | №задачи и схемы на рис.15 | Варианты | F1,кН | F2,кН | А1см2 | А2,см2 |
| 1 | 00 | 10 | 20 | 1,2 | 0,8 | 2 | 01 | 3,3 | 8,0 | 0,4 | 0,5 |
| 12 | 12 | 10 | 1,2 | 0,8 | 19 | 4 | 9,2 | 0,5 | 0,6 | ||
| 27 | 12 | 20 | 0,7 | 0,9 | 29 | 4,8 | 10,0 | 0,4 | 0,8 | ||
| 31 | 21 | 40 | 2,4 | 2,2 | 30 | 5,0 | 9,8 | 0,5 | 1,0 | ||
| 49 | 16 | 13 | 2,6 | 1,6 | 39 | 7,2 | 15,0 | 0,6 | 1,5 | ||
| 58 | 18 | 23 | 1,8 | 1,4 | 59 | 5,6 | 8,6 | 0,7 | 2,0 | ||
| 63 | 15 | 13 | 2,6 | 2,0 | 61 | 7,2 | 14,0 | 0,8 | 2,4 | ||
| 71 | 14 | 22 | 3,5 | 2,3 | 74 | 14,4 | 14,4 | 0,9 | 2,5 | ||
| 82 | 13 | 18 | 4,4 | 3,0 | 80 | 9,0 | 22,0 | 1,0 | 3,0 | ||
| 93 | 15 | 25 | 2,3 | 1,4 | 97 | 14,4 | 28,0 | 1,2 | 3,2 | ||
| 3 | 02 | 15 | 30 | 2,1 | 1,6 | 4 | 03 | 0,8 | 29 | 1,8 | 2,0 |
| 11 | 14 | 18 | 2,3 | 2,1 | 17 | 8 | 18 | 2,0 | 3,0 | ||
| 23 | 20 | 32 | 2,5 | 2,2 | 22 | 7,6 | 20,5 | 2,8 | 3,2 | ||
| 33 | 30 | 36 | 2,4 | 1,6 | 32 | 17,6 | 43,2 | 3,0 | 3,2 | ||
| 42 | 26 | 15 | 2,0 | 1,3 | 41 | 9,9 | 22,7 | 3,2 | 3,5 | ||
| 56 | 30 | 40 | 2,2 | 2,0 | 57 | 17,0 | 51,0 | 3,5 | 4,0 | ||
| 62 | 33 | 14 | 2,4 | 1,5 | 60 | 23,1 | 40,5 | 3,8 | 4,2 | ||
| 70 | 14 | 34 | 1,9 | 1,3 | 7 | 12,0 | 39,0 | 4,0 | 4,5 | ||
| 84 | 15 | 31 | 1,8 | 1,2 | 87 | 11 | 32 | 3,9 | 4,1 | ||
| 91 | 24 | 50 | 1,4 | 0,8 | 95 | 39,2 | 88 | 5,0 | 5,2 | ||
| 5 | 05 | 3,5 | 12,0 | 2,5 | 1,8 | 6 | 04 | 6 | 3 | 0.4 | 0.8 |
| 14 | 27 | 27 | 2,8 | 2,0 | 15 | 3 | 6 | 0.5 | 0.9 | ||
| 25 | 18 | 38 | 3,0 | 1,8 | 24 | 6 | 3 | 0.4 | 0.8 | ||
| 35 | 1,4 | 20 | 2,6 | 1,5 | 34 | 9 | 9 | 0.8 | 1.2 | ||
| 44 | 15 | 35 | 3,2 | 2,6 | 43 | 8.6 | 16 | 0.6 | 1.5 | ||
| 54 | 12 | 28 | 2,9 | 1,6 | 55 | 8,1 | 15 | 0.7 | 1.4 | ||
| 67 | 14 | 29 | 3,4 | 2,5 | 65 | 12 | 4 | 8 | 2.4 | ||
| 73 | 13 | 24 | 2,8 | 2,0 | 76 | 11 | 5 | 0.9 | 2.5 | ||
| 83 | 19 | 22 | 3,0 | 2,5 | 86 | 13 | 5 | 2 | 3 | ||
| 92 | 21 | 45 | 2,5 | 3,0 | 96 | 16 | 7 | 1 | 2.4 | ||
| 7 | 07 | 16 | 8 | 1.4 | 0.4 | 8 | 0.6 | 14 | 16 | 2.4 | 2.8 |
| 13 | 8.3 | 35 | 1.5 | 0.8 | 18 | 16 | 12 | 1.1 | 3 | ||
| 21 | 19 | 9.8 | 0.9 | 0.6 | 26 | 10 | 16 | 2.2 | 3 | ||
| 37 | 8 | 8.4 | 2 | 1.4 | 36 | 6.2 | 17.6 | 3 | 3.2 | ||
| 46 | 5 | 20 | 1.5 | 1.0 | 45 | 11.8 | 16.4 | 3.2 | 3.5 | ||
| 52 | 8 | 15 | 1.8 | 1.0 | 53 | 12.8 | 27.7 | 3.5 | 4 | ||
| 66 | 12.4 | 24 | 2.5 | 2.0 | 64 | 14.4 | 18.8 | 3.8 | 4.2 | ||
| 72 | 16 | 5.2 | 1 | 0.7 | 79 | 8.4 | 18.6 | 4 | 4.5 | ||
| 81 | 21.6 | 6 | 3.4 | 3.0 | 89 | 11 | 18 | 4.5 | 4.8 | ||
| 90 | 30.5 | 10 | 2.5 | 1.6 | 94 | 30 | 16 | 5 | 5.6 | ||
| 9 | 09 | 22.0 | 30.6 | 2.7 | 2.1 | 10 | 08 | 12 | 30.0 | 2.1 | 2.5 |
| 10 | 10.8 | 30 | 2.8 | 2.4 | 16 | 14.0 | 40.0 | 2.0 | 2.0 | ||
| 20 | 12.0 | 34 | 2.2 | 1.8 | 28 | 14.2 | 30.0 | 1.5 | 2.4 | ||
| 38 | 11.0 | 24 | 2.0 | 1.6 | 40 | 25.0 | 37.5 | 1.0 | 2.8 | ||
| 48 | 22.4 | 2.4 | 3.0 | 2.4 | 47 | 40.0 | 12.0 | 1.6 | 2.6 | ||
| 50 | 18.9 | 45.3 | 3.0 | 2.6 | 51 | 30.4 | 13.4 | 1.5 | 2.8 | ||
| 68 | 30.8 | 15.3 | 3.0 | 2.3 | 69 | 20.4 | 10.2 | 0.8 | 1.5 | ||
| 75 | 22.8 | 4.4 | 2.8 | 2.2 | 78 | 24 | 804 | 0.8 | 1.4 | ||
| 85 | 36.8 | 11.8 | 3.2 | 2.1 | 88 | 30.0 | 5.4 | 2.2 | 3.1 | ||
| 98 | 29.6 | 5.6 | 3.5 | 3.1 | 99 | 22 | 12 | 1.0 | 2.0 |
1 2 3 4 5
 |  |  |  |  |
 |  |  |  |  |
6 7 8 9 10
Методические указания к выполнению задания 6.
Вращающиеся детали (чаще всего это валы) испытывают деформацию – кручение: касательное относительное вращение поперечных сечений. Противодействие сечений вала кручению определяется крутящим моментом Мк и касательным напряжением
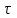 .
.Чтобы вал упруго сопротивлялся кручению, крутящий момент сечения должен уравновесить вращающие моменты справа или слева от сечения(
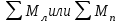 ), то есть
), то есть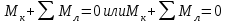
Результат будет одинаков, ибо левая и правая части действуют равным образом друг на друга по принципу равенства действия и противодействия.
Однако крутящий момент недостаточно характеризует сопротивление вала кручению. Очевидно вал меньшего диаметра с тем же крутящим моментом имеет меньшее сопротивление. Поэтому для достаточной оценки сопротивляемости вала кручению применяют другой параметр – касательное напряжение
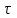 . Касательное напряжение учитывает величины: крутящего момента Мк, диаметр вала d, площадь сечения (круга)
. Касательное напряжение учитывает величины: крутящего момента Мк, диаметр вала d, площадь сечения (круга)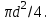
Формула касательного напряжения
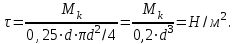
Рабочие напряжения
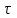 , возникающие в сечении вала при кручении, не должны превышать допустимые
, возникающие в сечении вала при кручении, не должны превышать допустимые 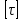 для данного материала. Условие прочности выражается зависимостью
для данного материала. Условие прочности выражается зависимостью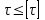 .
.Для установления наиболее нагруженного участка ступенчатого вала строят эпюру касательных напряжений.
Пример 6. Определить из условия прочности диаметр стального вала постоянного сечения, нагруженного вращающими моментами М1, М2, М3, М4, (рис. 16) при угловой скорости
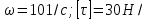 мм2
мм2
, мощности Р1=90 кВт, Р2=60кВт, Р4=30кВт.
 рис.16
рис.16 рис.17
рис.17Решение
1.Разбиваем вал на три участка – по сечениям, в которых приложены вращающие моменты.
2.Находим вращающие моменты
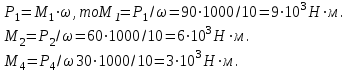
Равномерное вращение обеспечивается условием
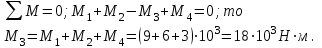
3.В любом сечении участка 1 в условиях прочности должен быть крутящий момент Мк1, уравновешивающий внешние справа (или слева) от сечения.
Справа –
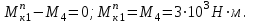
Слева -
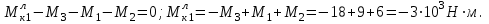
Крутящие моменты равны, поэтому можно строить эпюру и справа и слева. Разные знаки крутящих моментов потому, что
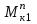 - это момент сопротивления левой части вала кручению правой, а
- это момент сопротивления левой части вала кручению правой, а 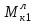 - момент сопротивления правой стороны кручению левой.
- момент сопротивления правой стороны кручению левой.Естественно они равны и противоположно направлены. Крутящий момент на втором участке
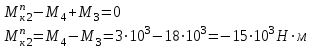
На третьем участке
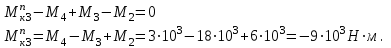
4.Строим эпюру. На всех участках крутящий момент есть постоянная функция – он не зависит от длины вала.
Следовательно, эпюра – прямая параллельная оси l – на первом участке(рис. 17) её координата Мк=3
 103Н
103Н м, на втором Мк=-15
м, на втором Мк=-15 103Н
103Н м, на третьемМк=-9
м, на третьемМк=-9 103Н
103Н м.
м.5.Определяем диаметр вала для наиболее напряжённого второго участка.