ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 25.10.2023
Просмотров: 66
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Лекция 7-8
Дискриминантный анализ
Дискриминантный анализ – это раздел математической статистики, содержанием которого является разработка методов решения задач различения объектов наблюдения по определенным признакам. Анализ очень удобен при обработке результатов тестирования отдельных лиц. Например, при выборе кандидатов на определенную должность можно всех опрашиваемых претендентов разделить на две группы: «подходит» и «не подходит». Еще один пример: для оценки финансового состояния своих клиентов при выдаче им кредита банк классифицирует их на надежных и ненадежных по ряду признаков. Таким образом, если возникает необходимость отнесения объекта к одному из реально существующих или выделенных определенным способом классов, тот можно воспользоваться дискриминантным анализом.
Все процедуры дискриминантного анализа можно разбить на две группы:
-
Первая группа позволяет интерпретировать различия между существующими классами. -
Вторая - проводить классификацию новых объектов в тех случаях, когда неизвестно заранее, к какому из существующих классов они принадлежат.
Пусть имеется множество единиц наблюдения. Каждая единица наблюдения характеризуется несколькими признаками (перменными). Xij – значение j-ой переменной у I-го объекта. I =1,…,N; j=1,…,p
Предположим, что все множество объектов разбито на несколько подмножеств (два и более). Из каждого подмножества взята выборка объемом nk , где k - номер подмножества (класса).
Признаки, которые используются для того, чтобы отличить один класс от другого, называются дискриминантными переменными. Каждая из этих переменных должна быть измерена по интервальной шкале.
Теоретически число дискриминантных переменных не ограничено, но на практике их выбор должен осуществляться на основании логического анализа исходной информации. Число объектов наблюдения должно превышать число дискриминантных переменных, как минимум на два, т.е. p<N. Дискриминантные переменные должны быть линейно независимыми. Еще одним предположением при дискриминантном анализе является нормальность закона распределения многомерной величины, т.е. каждая из дискриминантных переменных внутри каждого из рассматриваемых классов должна быть подчинена нормальному закону распределения.
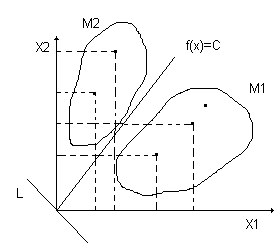
Геометрическая интерпретация алгоритма дискриминантного анализа
Имеются два множества M1 и M2. Каждый объект характеризуется (в данном случае) двумя переменными x1 и x2. если рассматривать проекции объектов (точек) на оси, то эти множества пересекаются. Чтобы наилучшим образом разделить два рассматриваемых множества, нужно построить соответствующую линейную комбинацию переменных x1 и x2. Для двумерного пространства эта задача сводится к определению новой системы координат. Причем новые оси должны быть расположены таким образом, чтобы проекции объектов, принадлежащих разным множествам на ось L, были максимально разделены. Ось С перпендикулярна оси L и разделяет два «облака» точек наилучшим образом, т.е. чтобы множества оказались по разные стороны от этой прямой. При этом вероятность ошибки классификации должна быть минимальной. Сформулированные условия должны быть учтены при определении коэффициентов a1 и a2 следующей функции: f(x)=a1x1+a2x2.
Функция f(x) называется канонической дискриминантной функцией, а x1 и x2 – дискриминантными переменными.
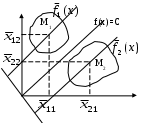
Обозначим Xij – среднее значение j-го признака у I-го множества (класса). Тогда для множества M1 среднее значение функции f1(x) будет равно
Для множества M2 среднее значение функции f2(x) равно
Геометрическая интерпретация этих функций – две параллельные прямые, проходящие через центры классов (множеств).
Дискриминантная функция может быть как линейной, так и нелинейной. Мы ограничимся рассмотрением линейной функции.
Коэффициенты дискриминантной функции определяются таким образом, чтобы
и 
как можно больше различались между собой, т.е. для двух множеств (классов) было максимальным выражение 
Вектор коэффициентов дискриминантной функции определяется из формулы:
. S – это объединенная ковариационная матрица 
. S1 – матрица отклонений наблюдаемых значений исходных переменных от их средних величин в первой группе. S2 – матрица отклонений наблюдаемых значений исходных переменных от их средних величин во второй группе.
и 
- векторы средних в первой и второй группах.Классификация при наличии двух обучающих выборок.
Перед тем как приступить к процедуре классификации, нужно определить границу, разделяющую в частном случае две рассматриваемые группы. Такой величиной может быть значение функции, равноудаленное от
и 
, т.е. 
Величина С называется константой дискриминации.
Пример. В качестве обучающих будем рассматривать две выборки, принадлежащие двум классам. Имеются данные по двум группам промышленных предприятий.
X1- фондоотдача производственных фондов, руб.
X2 – затраты на рубль произведенной продукции, коп.
X3 – затраты материалов и сырья на рубль продукции, коп.
| | Номер предприятия | X1 | X2 | X3 |
| 1 группа | 1 | 0,50 | 94,00 | 8,50 |
| 2 | 0,67 | 75,4 | 8,79 | |
| 3 | 0,68 | 85,2 | 9,10 | |
| 4 | 0,55 | 98,8 | 8,47 | |
| 2 группа | 5 | 1,52 | 81,50 | 4,95 |
| 6 | 1,20 | 93,8 | 6,95 | |
| 7 | 1,46 | 86,50 | 4,70 |
Необходимо провести классификацию четырех новых предприятий, имеющих следующие значения исходных переменных:
1-е предприятие: X1=1,07; X2=93,5; X3=5,30
2-е предприятие: X1=0,99; X2=84,0; X3=4,85
3-е предприятие: X1=0,70; X2=76,80; X3=3,50
4-е предприятие: X1=1,24; X2=88,0; X3=4,95
Для удобства запишем значения исходных переменных для каждой группы предприятий в виде матриц:
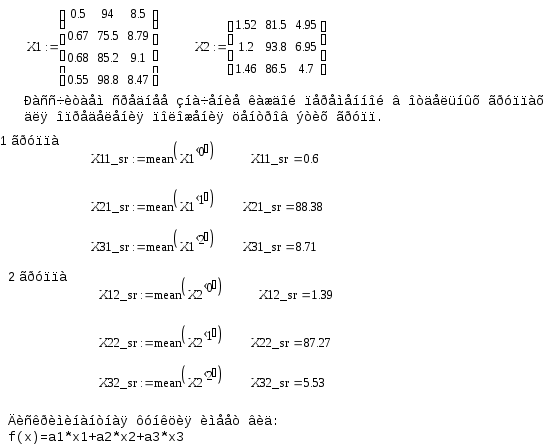
Коэффициенты a1, a2, a3 вычисляются по формуле
, 
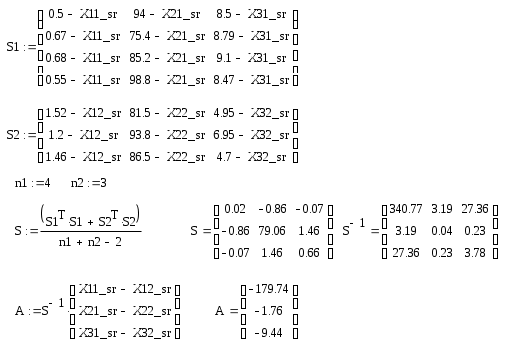
Таким образом, a1= -179.74; a2= -1.764; a3= -9.44. Подставим значения коэффициентов в формулу f(x)=a1*x1+a2*x2+a3*x3 и рассчитаем значения дискриминантной функции для каждого объекта.
Для 1-го множества:
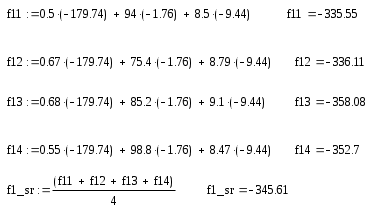
Для 2-го множества:
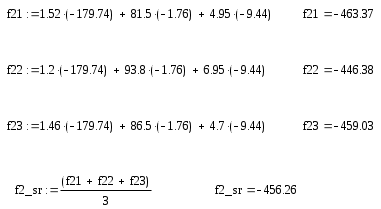
Тогда константа дискриминации будет равна:
После получения константы дискриминации можно проверить правильность распределения объектов в уже существующих классах, а также провести классификацию новых объектов.
Рассмотрим новые объекты 1, 2, 3 и 4.
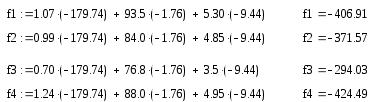
Объекты 2 и 3 относятся к первому классу (f2>C, f3>C); Объекты 1 и 4 относятся ко второму классу (f1
Дискриминантный анализ относится к методам многомерной классификации. В ходе дискриминантного анализа формулируется правило, по которому новые единицы совокупности относятся к одному из уже существующих классов. Основанием для отнесения каждой единицы совокупности к определенному множеству служит величина дискриминантной функции.
Основными проблемами дискриминантного анализа являются
-
Определение набора дискриминантных переменных -
Выбор вида дискриминантной функции
Кластерный анализ
Задача кластерного анализа состоит в разбиении исходной совокупности объектов на группы схожих, близких между собой объектов. Эти группы называют кластерами. Другими словами, кластерный анализ это один из способов классификации объектов по признакам. Разбиение по группам происходит с учетом всех группировочных признаков одновременно. Желательно, чтобы результаты классификации имели содержательную интерпретацию. Кластерный анализ находит применение в различных областях: медицина, маркетинговые исследования. Фактически, кластерный анализ является «набором» различных алгоритмов распределения объектов по кластерам.
Если данные понимать как точки в признаковом пространстве, то задача кластерного анализа формулируется как выделение "сгущений точек", разбиение совокупности на однородные подмножества объектов.
При проведении кластерного анализа обычно определяют расстояние на множестве объектов; алгоритмы кластерного анализа формулируют в терминах этих расстояний. Мер близости и расстояний между объектами существует великое множество. Их выбирают в зависимости от цели исследования. В частности, евклидово расстояние лучше использовать для количественных переменных, расстояние хи-квадрат - для исследования частотных таблиц, имеется множество мер для бинарных переменных.
Кластерный анализ является описательной процедурой, он не позволяет сделать никаких статистических выводов, но дает возможность провести своеобразную разведку - изучить "структуру совокупности".
Одна из концепций кластеризации состоит в построении разбиения исходного множества объектов, доставляющего оптимальное значение определенной целевой функции. Большинство алгоритмов кластеризации основано на эвристических методах. Дать рекомендации для выбора того или иного метода кластеризации можно только в общих чертах.
Пусть
- объекты, каждый их которых задан набором p признаков. Распределения объектов по кластерам на однородные в некотором смысле группы должно удовлетворять критерию оптимальности, который выражается в терминах расстояния 
между любой парой объектов рассматриваемой совокупности.В качестве расстояния (метрики) может быть взята любая действительная функция