ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 25.10.2023
Просмотров: 67
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Затем заново вычисляются центры этих кластеров, которыми после этого момента считаются покоординатные средние кластеров. После этого опять перераспределяются объекты. Вычисление центров и перераспределение объектов происходит до тех пор, пока центры не стабилизируются.
Этот метод относится к итерационным методам. Сущность итерационных методов заключается в том. Что процесс кластеризации начинается с задания некоторых начальных условий (количество образуемых кластеров, порог завершения процесса кластеризации и.т.д.). итеративные методы требуют от пользователя больше интуиции при выборе типа классификационных процедур и задания начальных условий разбиения.
В отличие от иерархических методов метод k-средних не требует хранения матрицы расстояний. Алгоритм этого метода предполагает использование только исходных данных.
Пусть имеется n наблюдений, каждое из которых характеризуется p признаками
. Эти наблюдения необходимо разбить на k кластеров. Для начала процедуры классификации должны быть заданы k случайно выбранных объектов, которые будут служить эталонами, т.е. центрами кластеров. Каждому эталону присваивается номер, который одновременно является и номером кластера. На первом шаге из оставшихся (n-k) объектов извлекается точка Xi с координатами 
и проверяется к какому из эталонов она находится ближе всего. Для этого используется одна из метрик, например, евклидово расстояние. Проверяемый объект к тому центру (эталону), которому соответствует 
. Эталон заменяется новым с учетом добавленной точки и вес его (количество объектов, входящих в данный кластер) увеличивается на 1. Эталон пересчитывается по формуле:
, L– номер итерации, j – номер эталона, 
- вес эталона. 
-вектор значений переменных для I-го объекта.Если встречаются два или более минимальных расстояния, то I-ый объект присоединяют к центру с наименьшим порядковым номером. Затем берут следующую точку и для нее повторяют все процедуры. Таким образом, через (n-k) шагов все объекты совокупности окажутся отнесенными к одному из k кластеров, но на этом процесс разбиения не заканчивается. Чтобы добиться устойчивости по тому же правилу, все точки (объекты) опять присоединяются к полученным кластерам, при этом веса продолжают накапливаться. Новое разбиение сравнивается с предыдущим, если они совпадают, то работа алгоритма заканчивается. Окончательное разбиение имеет центры тяжести, которые не совпадают с эталонами.
Реализация метода k-средних в пакете SPSS (k-means)
Часто переменные, используемые в кластеризации, имеют разный диапазон изменений, так как измерены они в различных шкалах или просто из-за того, что характеризуют разные свойства объектов (например, рост и вес, килограммы и граммы). В этих условиях основное влияние на кластеризацию окажут переменные, имеющие большую дисперсию. Поэтому перед кластеризацией полезно стандартизовать переменные. К сожалению, в данной команде кластерного анализа средства стандартизации не предусмотрены непосредственно, как в процедуре иерархического кластерного анализа.
Говоря о допустимом уровне измерения для переменных, используемых при кластеризации необходимо помнить, команда использует только евклидово расстояние. Следовательно, корректные результаты при применении данного метода можно ожидать только при применении метрических переменных.
Команда использует только евклидово расстояние. При этом, часть переменных может иметь неопределенные значения, расстояния до центров определяются по определенным значениям. Для использования такой возможности в меню Options следует выбрать параметр обработки пропущенных данных PAIRWISE.
Ключевым вопросом, который необходимо решить при подготовке к выполнению кластерного анализа, является вопрос о количестве получаемых кластеров. В силу специфики алгоритма, в отличии от иерархического кластерного анализа, в данном случае в обязательном порядке требуется задать количество получаемых кластеров. (По умолчанию алгоритм предлагает делить на 2 кластера – см. рисунок 5.10)
Критерии качества классификации
После завершения процедуры классификации необходимо оценить полученные результаты. Для этой цели используется мера качества классификации, которою принято называть функционалом или критерием качества. Наилучшим считается такое разбиение на классы, при котором достигается экстремальное значение целевой функции – функционала качества.
Наиболее распространенные функционалы качества:
-
Сумма квадратов расстояний до центров классов. Разбиение оптимально, если значение этого функционала будет минимальным -
Суммарная внутриклассовая дисперсия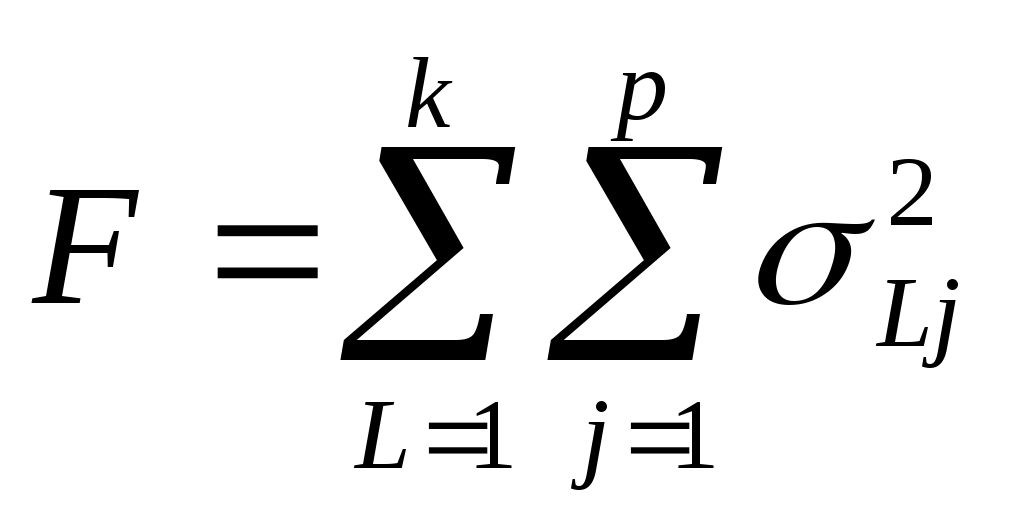
, где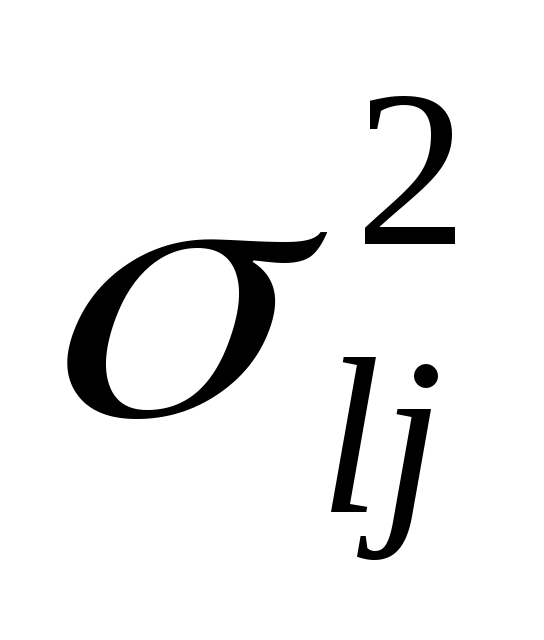 
- дисперсия j-ой переменной в кластере SL. Разбиение оптимально, если значение этого функционала будет минимальным. Существует несколько алгоритмов кластеризации, обеспечивающих оптимальное разбиение с точки зрения этого функционала. К ним относится метод k-средних.
Судить о качестве разбиения позволяют некоторые приемы: сравнение средних значений признаков в отдельных кластерах со средними значениями признаков во всей совокупности объектов. Если отличие существенно, то можно говорить о хорошем разбиении.
Факторный анализ
Социологический смысл модели факторного анализа состоит в том, что измеряемые нами эмпирические показатели, переменные являются следствием некоторых других, глубинных, скрытых от непосредственного измерения характеристик – латентных переменных. Действительно, если мы фиксируем, степень доверия респондента к различным государственным институтам, то вполне логично предположить, что нет каких отдельных «доверий» к Государственной Думе, Совету Федерации, Счетной Палате и т.п. Скорее у респондента есть некоторое общее отношение к институтам центральной власти, которое и определяет то, как респондент отвечает на отдельные вопросы по доверию к каждому отдельному институту.
Существенно при этом, что это общее, единое отношение к государственным институтам, формируя отношение к каждому из них, не определяет отношения к отдельному институту на 100%. Таким образом, ответ респондента на вопрос о том, насколько он доверяет какому-то конкретному государственному институту, находится под влиянием двух составляющих: общего фактора отношения к государственным институтам и отдельного отношения именно к данному конкретному институту.
Идея метода состоит в сжатии матрицы признаков в матрицу с меньшим числом переменных, сохраняющую почти ту же самую информацию, что и исходная матрица. В основе моделей факторного анализа лежит гипотеза, что наблюдаемые переменные являются косвенными проявлениями небольшого числа скрытых (латентных) факторов. Хотя такую идею можно приписать многим методам анализа данных, обычно под моделью факторного анализа понимают представление исходных переменных в виде линейной комбинации факторов. Схематично такой взгляд на формирование ответов респондентов на вопросы анкеты показан на рисунке 5.1.
Рисунок 5.1
Условное представление модели факторного анализа
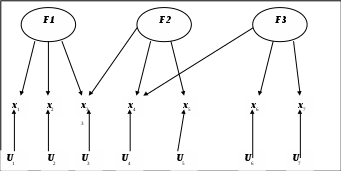
На рисунке 5.1 F1, F2, F3 – факторы, каждый из которых влияет на определенную совокупность переменных; x1, x2,.. ,x7 – переменные, формируемые на основании ответов опрашиваемых;
U1, U2,...,U7 – уникальные факторы, влияющие на соответствующие переменные.
Факторы F построены так, чтобы наилучшим способом (с минимальной погрешностью) представить Х. В этой модели "скрытые" переменные Fk называются общими факторами, а переменные Ui специфическими факторами ("специфический" -это лишь один из переводов применяемого в англоязычной литературе слова Unique, в отечественной литературе в качестве определения Ui встречаются также слова "характерный", "уникальный"). Значения aik называются факторными нагрузками.
Обычно (хотя и не всегда) предполагается, что Xi стандартизованы (
=1, Xi=0), а факторы F1,F2,…,Fm независимы и не связаны со специфическими факторами Ui (хотя существуют модели, выполненные в других предположениях). Предполагается также, что факторы Fi стандартизованы.В этих условиях факторные нагрузки aik совпадают с коэффициентами корреляции между общими факторами и переменными Xi. Дисперсия Xi раскладывается на сумму квадратов факторных нагрузок и дисперсию специфического фактора:
, где 
Величина
называется общностью, 
- специфичностью. Другими словами, общность представляет собой часть дисперсии переменных, объясненную факторами, специфичность - часть не объясненной факторами дисперсии.В соответствии с постановкой задачи, необходимо искать такие факторы, при которых суммарная общность максимальна, а специфичность - минимальна.
Метод главных компонент
Один из наиболее распространенных методов поиска факторов, метод главных компонент, состоит в последовательном поиске факторов. Вначале ищется первый фактор, который объясняет наибольшую часть дисперсии, затем независимый от него второй фактор, объясняющий наибольшую часть оставшейся дисперсии, и т.д. Математическая реализация метода главных компонент достаточно сложна, поэтому для пояснения идеи метода мы прибегнем к ее условному изображению (рисунок 5.2).