ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 25.10.2023
Просмотров: 68
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
, определенная на множестве 
и удовлетворяющая следующим условиям:
Выбор расстояния неоднозначен и в этом состоит вся сложность.
Наиболее популярной метрикой является евклидова. Эта метрика отвечает интуитивным представлениям близости. При этом на расстояние между объектами могут сильно влиять изменения масштабов. Например, если один из признаков был измерен в метрах, а затем его значения переведены в сантиметры, то евклидово расстояние сильно изменится и это приведет к тому, что результаты кластерного анализа могут значительно отличаться от предыдущих.
Если признаки измерены в разных единицах измерения, то требуется их предварительная нормировка. – такое преобразование исходных данных, которое приводит их в безразмерные величины.
Наиболее известные способы нормировки:
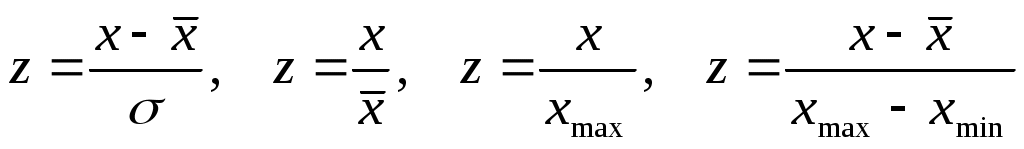
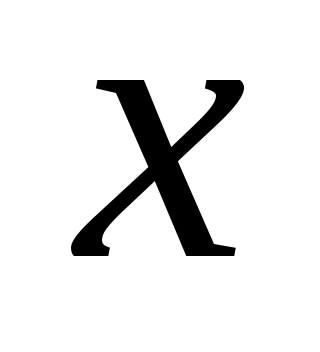- исходное значение, 
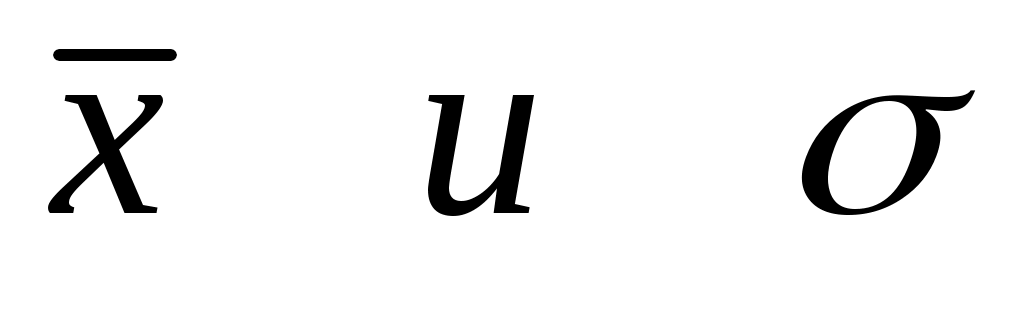-среднее и среднее квадратическое отколонение.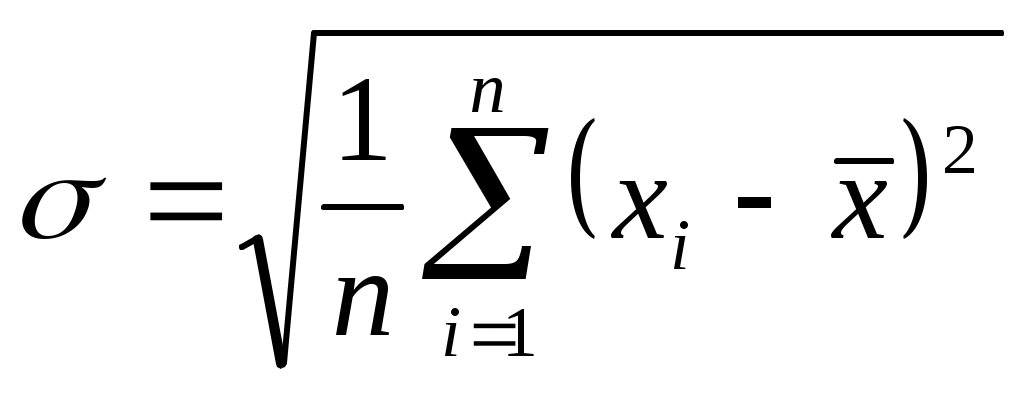 
Наиболее употребительные метрики:
Выбор меры расстояния и весов для классифицирующих переменных – очень важный этап кластерного анализа, так как от этих процедур зависят состав и количество формируемых кластеров, а также степень сходства объектов внутри кластеров.
Пример: Определим сходство меду предприятиями, если каждое из них характеризуется тремя признаками – производство продукции (млрд.руб.), стоимость основных производственных фондов (млрд.руб.), фонд заработной платы (млрд.руб.).
Матрица евклидовых расстояний
Самые близкие объекты 1 и 2 (расстояние=8,81), самые дальние объекты 3 и 4 (расстояние=31,57)
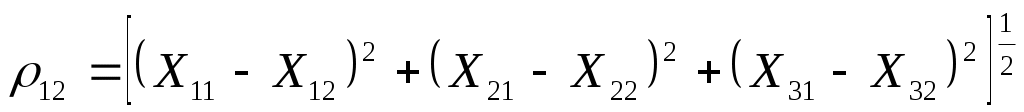
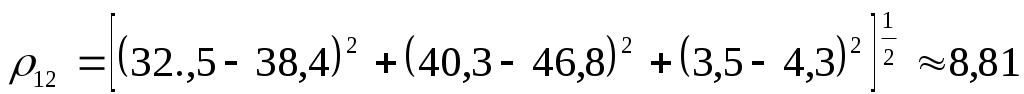
Нормируем значения
Матрица стандартизованных значений признаков
Матрица евклидовых расстояний
Самые близкие объекты 2 и 4 (расстояние=0,56), самые дальние объекты 3 и 2 (расстояние=13,2)
Иерархический кластерный анализ
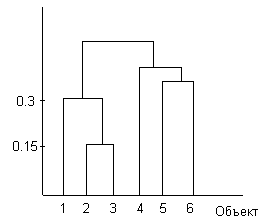
Сущность этого метода заключается в том, что на первом шаге каждый объект выборки рассматривается как отдельный кластер. Процесс объединения кластеров происходит последовательно: на основании матрицы расстояний объединяются более близкие объекты. Этот процесс может быть представлен графически в виде дендрограммы. (граф-дерево).
Дендрограмма показывает, что на первом шаге были объединены в один кластер объекты n2 и n3. Расстояние между ними 0,15. На втором шаге к ним присоединился объект n1. Расстояние от первого объекта до кластера равно 0,3 и т.д.
Метод одиночной связи
На основании матрицы расстояний определяются два наиболее близких (схожих) объекта. Они образуют первый кластер. На следующем шаге выбирается объект, который будет включен в этот кластер. Этот объект будет иметь наибольшее сходство хотя бы с одним из уже включенных объектов в этот кластер.
Пример.
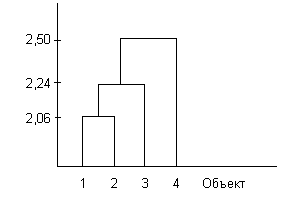
В первый кластер будут включены 1 и 2 объекты, так как расстояние между ними наименьшее 2,06. На следующем шаге к этому кластеру будет подключен третий объект, так как расстояние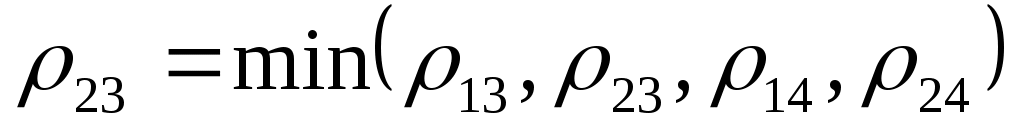
. На последнем шаге будет добавлен 4 объект.
Метод полных связей
Включение нового объекта в кластер происходит в том случае, если расстояние между объектами меньше некоторого заданного уровня.
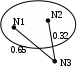
Если задано предельное расстояние 0,3, то третий объект не будет включен в кластер, так как 0.65>0.3 и 0.32>0.3.
Если задано предельное расстояние 0,7, то третий объект будет включен в кластер, так как 0.65<0.7 и 0.32<0.7.
Метод средних связей
Для решения вопроса о включении в кластер вычисляется среднее расстояние, которое затем сравнивается с пороговым уровнем. Например, (0.65+0.23)/2=0.485>0.3 – третий объект не будет включен в кластер.
Если речь идет об объединении двух кластеров, то вычисляют расстояние между их центрами и сравнивают его с пороговым значением.
Алгоритм кластеризации можно представить в виде последовательности процедур:
Мера сходства для объединения двух кластеров определяется следующими методами:
Метод кластеризации k-средних
Процедура иерархического кластерного анализа хороша для малого числа объектов. Ее преимущество в том, что каждый объект можно, образно говоря, пощупать руками. Но эта процедура не годится для огромных социологических данных из-за трудоемкости агломеративного алгоритма и слишком большого размера и практической бессмысленности дендрограмм.
В такой ситуации наиболее приемлем алгоритм, носящий название метода "k-средних". Он реализуется в пакете командой меню k-means.
Алгоритм заключается в следующем: выбирается заданное число k- точек и на первом шаге эти точки рассматриваются как "центры" кластеров. Каждому кластеру соответствует один центр. Объекты распределяются по кластерам по такому принципу: каждый объект относится к кластеру с ближайшим к этому объекту центром. Таким образом, все объекты распределились по k кластерам.
и удовлетворяющая следующим условиям:-
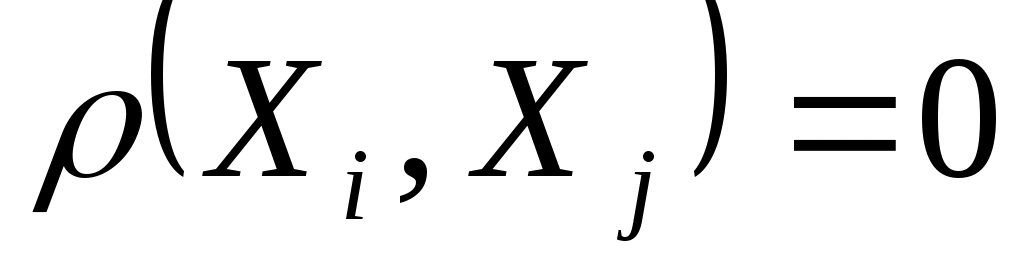тогда и только тогда, когда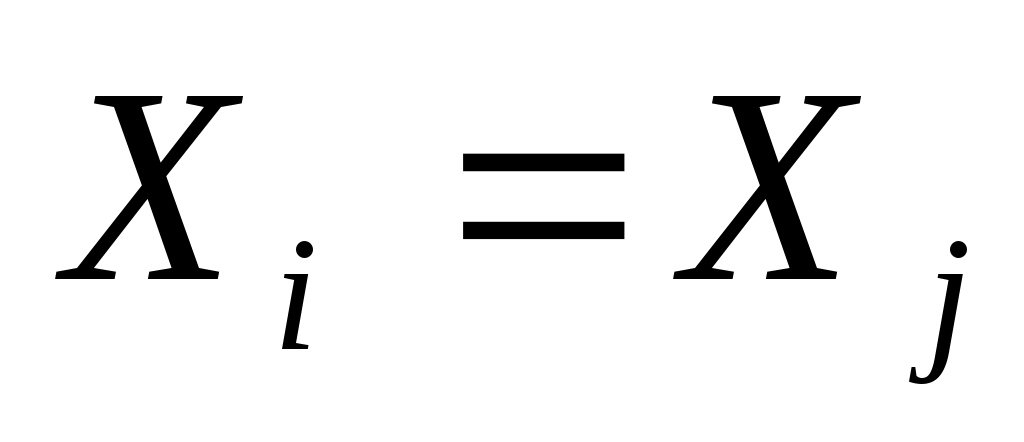 
-
-
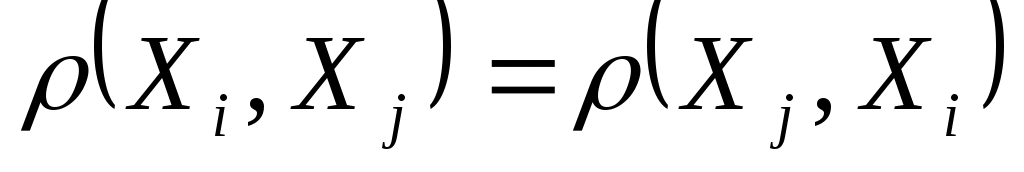
Выбор расстояния неоднозначен и в этом состоит вся сложность.
Наиболее популярной метрикой является евклидова. Эта метрика отвечает интуитивным представлениям близости. При этом на расстояние между объектами могут сильно влиять изменения масштабов. Например, если один из признаков был измерен в метрах, а затем его значения переведены в сантиметры, то евклидово расстояние сильно изменится и это приведет к тому, что результаты кластерного анализа могут значительно отличаться от предыдущих.
Если признаки измерены в разных единицах измерения, то требуется их предварительная нормировка. – такое преобразование исходных данных, которое приводит их в безразмерные величины.
Наиболее известные способы нормировки:
- исходное значение, -среднее и среднее квадратическое отколонение. Наиболее употребительные метрики:
-
евклидова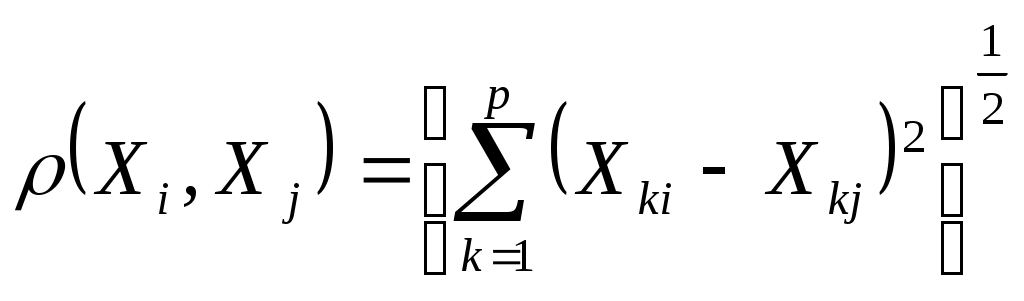
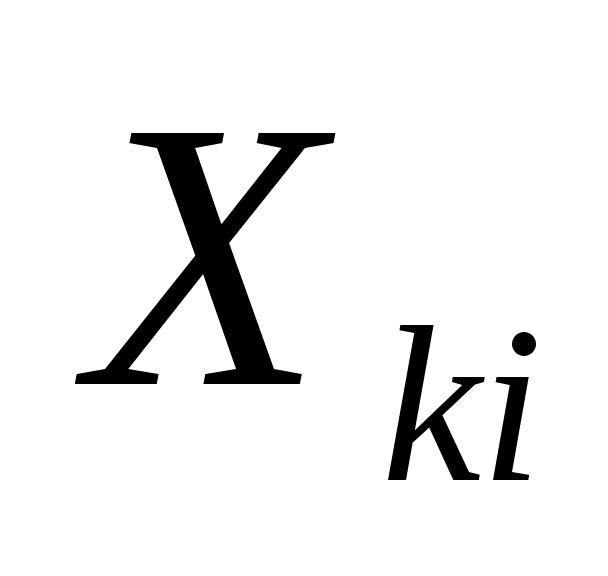-значение k-го признака I-го объекта; -
взвешенная евклидова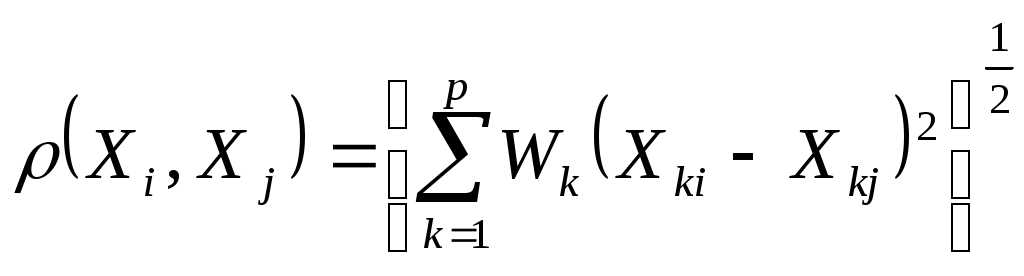
, 
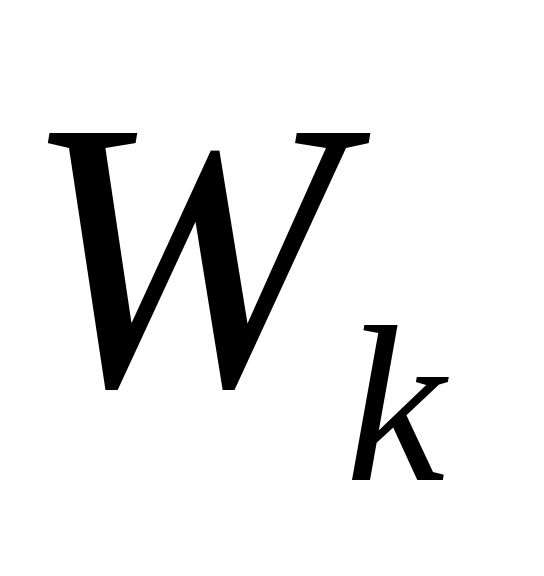- вес
k-го признака. Веса задаются пропорционально степени важности переменных.
Выбор меры расстояния и весов для классифицирующих переменных – очень важный этап кластерного анализа, так как от этих процедур зависят состав и количество формируемых кластеров, а также степень сходства объектов внутри кластеров.
Пример: Определим сходство меду предприятиями, если каждое из них характеризуется тремя признаками – производство продукции (млрд.руб.), стоимость основных производственных фондов (млрд.руб.), фонд заработной платы (млрд.руб.).
Матрица исходных данных
| № | X1 | X2 | X3 |
| 1 | 32,5 | 40,3 | 3,5 |
| 2 | 38,4 | 46,8 | 4,3 |
| 3 | 16,7 | 25,7 | 2,0 |
| 4 | 42,3 | 44,0 | 4,5 |
Матрица евклидовых расстояний
| № | 1 | 2 | 3 | 4 |
| 1 | 0 | 8,81 | 21,55 | 10,36 |
| 2 | | 0 | 30,35 | 30,48 |
| 3 | | | 0 | 31,57 |
| 4 | | | | 0 |
Самые близкие объекты 1 и 2 (расстояние=8,81), самые дальние объекты 3 и 4 (расстояние=31,57)
Нормируем значения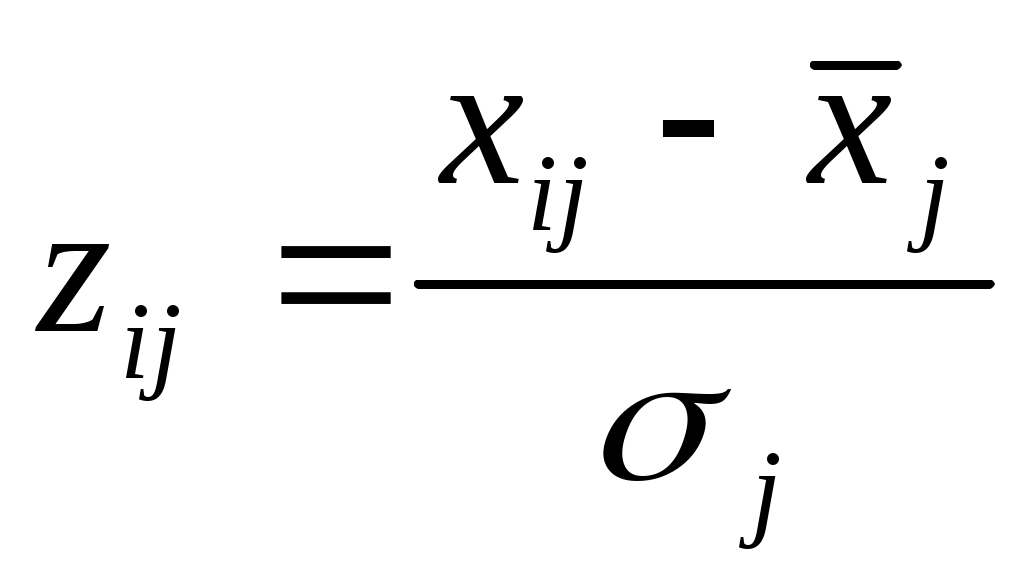 
Матрица стандартизованных значений признаков
| № | X1 | X2 | X3 | | | |
| 1 | 32,5 | 40,3 | 3,5 | 0,000625 | 1,21 | 0,005625 |
| 2 | 38,4 | 46,8 | 4,3 | 35,10563 | 57,76 | 0,525625 |
| 3 | 16,7 | 25,7 | 2 | 248,8506 | 182,25 | 2,480625 |
| 4 | 42,3 | 44 | 4,5 | 96,53062 | 23,04 | 0,855625 |
| Средние | 32,475 | 39,2 | 3,575 | 380,4875 | 264,26 | 3,8675 |
| Средние квадратические отклонения | 9,753044 | 8,128038 | 0,983298 | | | |
| Нормированные | Z1 | Z2 | Z3 | | | |
| | 0,002563 | 0,135334 | -0,07627 | | | |
| | 0,607503 | 0,935035 | 0,737315 | | | |
| | -1,61744 | -1,66092 | -1,60175 | | | |
| | 1,007378 | 0,590548 | 0,940712 | | | |
| № | X1 | X2 | X3 | | |
| 1 | 32,5 | 40,3 | 3,5 | =(B2-$B$6)^2 | =(C2-$C$6)^2 |
| 2 | 38,4 | 46,8 | 4,3 | =(B3-$B$6)^2 | =(C3-$C$6)^2 |
| 3 | 16,7 | 25,7 | 2 | =(B4-$B$6)^2 | =(C4-$C$6)^2 |
| 4 | 42,3 | 44 | 4,5 | =(B5-$B$6)^2 | =(C5-$C$6)^2 |
| Средние | =СРЗНАЧ(B2:B5) | =СРЗНАЧ(C2:C5) | =СРЗНАЧ(D2:D5) | =СУММ(E2:E5) | =СУММ(F2:F5) |
| Средние квадратические отклонения | =КОРЕНЬ(1/4*E6) | =КОРЕНЬ(1/4*F6) | =КОРЕНЬ(1/4*G6) | | |
| Нормированные | Z1 | Z2 | Z3 | | |
| 1 | =(B2-$B$6)/$B$7 | =(C2-$C$6)/$C$7 | =(D2-$D$6)/$D$7 | | |
| 2 | =(B3-$B$6)/$B$7 | =(C3-$C$6)/$C$7 | =(D3-$D$6)/$D$7 | | |
| 3 | =(B4-$B$6)/$B$7 | =(C4-$C$6)/$C$7 | =(D4-$D$6)/$D$7 | | |
| 4 | =(B5-$B$6)/$B$7 | =(C5-$C$6)/$C$7 | =(D5-$D$6)/$D$7 | | |
Матрица евклидовых расстояний
| № | 1 | 2 | 3 | 4 |
| 1 | 0 | 1,29 | 2,86 | 1,5 |
| 2 | | 0 | 13,2 | 0,56 |
| 3 | | | 0 | 4,3 |
| 4 | | | | 0 |
Самые близкие объекты 2 и 4 (расстояние=0,56), самые дальние объекты 3 и 2 (расстояние=13,2)
Иерархический кластерный анализ
Сущность этого метода заключается в том, что на первом шаге каждый объект выборки рассматривается как отдельный кластер. Процесс объединения кластеров происходит последовательно: на основании матрицы расстояний объединяются более близкие объекты. Этот процесс может быть представлен графически в виде дендрограммы. (граф-дерево).
Дендрограмма показывает, что на первом шаге были объединены в один кластер объекты n2 и n3. Расстояние между ними 0,15. На втором шаге к ним присоединился объект n1. Расстояние от первого объекта до кластера равно 0,3 и т.д.
Метод одиночной связи
На основании матрицы расстояний определяются два наиболее близких (схожих) объекта. Они образуют первый кластер. На следующем шаге выбирается объект, который будет включен в этот кластер. Этот объект будет иметь наибольшее сходство хотя бы с одним из уже включенных объектов в этот кластер.
Пример.
| № | 1 | 2 | 3 | 4 |
| 1 | 0 | 2,06 | 4,03 | 2,5 |
| 2 | | 0 | 2,24 | 4,12 |
| 3 | | | 0 | 6,32 |
| 4 | | | | 0 |
В первый кластер будут включены 1 и 2 объекты, так как расстояние между ними наименьшее 2,06. На следующем шаге к этому кластеру будет подключен третий объект, так как расстояние
. На последнем шаге будет добавлен 4 объект. Метод полных связей
Включение нового объекта в кластер происходит в том случае, если расстояние между объектами меньше некоторого заданного уровня.
Если задано предельное расстояние 0,3, то третий объект не будет включен в кластер, так как 0.65>0.3 и 0.32>0.3.
Если задано предельное расстояние 0,7, то третий объект будет включен в кластер, так как 0.65<0.7 и 0.32<0.7.
Метод средних связей
Для решения вопроса о включении в кластер вычисляется среднее расстояние, которое затем сравнивается с пороговым уровнем. Например, (0.65+0.23)/2=0.485>0.3 – третий объект не будет включен в кластер.
Если речь идет об объединении двух кластеров, то вычисляют расстояние между их центрами и сравнивают его с пороговым значением.
Алгоритм кластеризации можно представить в виде последовательности процедур:
-
Значения исходных переменных нормируются одним из способов -
Рассчитывается матрица расстояний -
Находится пара самых близких кластеров. Эти кластеры объединяются. Новому кластеру присваивается меньший из номеров объединяемых кластеров -
процедуры 2 и 3 повторяются до тех пор, пока не будет получен один кластер или до достижения заданного порога сходства.
Мера сходства для объединения двух кластеров определяется следующими методами:
-
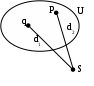
Метод ближайшего соседа – степень сходства оценивается по степени сходства между наиболее схожими (близкими) объектами. Если d1>d2, то S войдет в кластер U по d2.
-
Метод дальнего соседа – степень сходства оценивается по степени сходства между наиболее несхожими (отдаленными) объектами. S войдет в кластер U по d1. -
Центроидная кластеризация – в обоих кластерах рассчитываются средние значения переменных. Затем расстояние между двумя кластерами рассчитывается как дистанция между двумя осредненными наблюдениями.
Метод кластеризации k-средних
Процедура иерархического кластерного анализа хороша для малого числа объектов. Ее преимущество в том, что каждый объект можно, образно говоря, пощупать руками. Но эта процедура не годится для огромных социологических данных из-за трудоемкости агломеративного алгоритма и слишком большого размера и практической бессмысленности дендрограмм.
В такой ситуации наиболее приемлем алгоритм, носящий название метода "k-средних". Он реализуется в пакете командой меню k-means.
Алгоритм заключается в следующем: выбирается заданное число k- точек и на первом шаге эти точки рассматриваются как "центры" кластеров. Каждому кластеру соответствует один центр. Объекты распределяются по кластерам по такому принципу: каждый объект относится к кластеру с ближайшим к этому объекту центром. Таким образом, все объекты распределились по k кластерам.