ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 25.10.2023
Просмотров: 69
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Смысл рисунка 5.2 в следующем. Для построения первого фактора берется прямая, проходящая через начало координат и облако рассеяния данных. Объектам можно сопоставить расстояния их проекций на эту прямую до центра координат, причем для одной из половин прямой (по отношению к нулевой точке) можно взять эти расстояния с отрицательным знаком. Такое построение представляют собой новую переменную, которую мы назовем осью. При построении фактора отыскивается такая ось, чтобы дисперсия переменных вокруг оси была минимальна. (Заметим, что в определенном смысле эта первая ось строится по той же модели, что регрессионная прямая в регрессионном анализе). Это означает, что этой осью объясняется максимум дисперсии переменных. Найденная ось после нормировки используется в качестве первого фактора. Если облако данных вытянуто в виде эллипсоида (имеет форму "огурца"), фактор совпадет с направлением, в котором вытянуты объекты, и по нему (по проекциям) с наибольшей точностью можно предсказать значения исходных переменных.
Рисунок 5.2
Условное представление модели главных компонент.
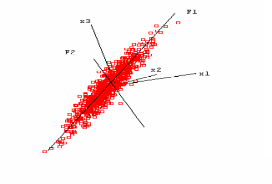
Для поиска второго фактора ищется ось, перпендикулярная первому фактору, также объясняющая наибольшую часть дисперсии, не объясненной первой осью. После нормировки эта ось становится вторым фактором. Если данные представляют собой плоский элипсоид ("блин") в трехмерном пространстве, два первых фактора позволяют в точности описать эти данные.
Максимально возможное число главных компонент равно количеству переменных. Иными словами, если мы хотим на 100% описать значения n переменных, то для этого потребуется столько же, то есть n главных компонент. Сколько главных компонент необходимо построить для оптимального представления рассматриваемых исходных переменных?
Обозначим k объясненную главной компонентой Fk часть суммарной дисперсии совокупности исходных факторов. По умолчанию, в пакете предусмотрено продолжать строить факторы, пока к>1. Напомним, что переменные стандартизованы, и поэтому нет смысла строить очередной фактор, если он объясняет часть дисперсии, меньшую, чем приходящуюся непосредственно на одну переменную. При этом следует учесть, что 1>2>3,….
К сведению читателя заметим, что значения
k являются собственными значениями корреляционной матрицы Xi, поэтому в выдаче они будут помечены текстом "EIGEN VALUE" (собственные значения).
Техника построения главных компонент расходится с теоретическими предположениями о факторах: имеется m+n независимых факторов, полученных методом главных компонент в n-мерном пространстве, что невозможно.
Интерпретация факторов.
Как же можно понять смысл того, что скрыто в найденных факторах? Основной информацией, которую использует исследователь, являются факторные нагрузки. Для интерпретации необходимо приписать каждому фактору какой-то термин, понятие. Этот термин появляется на основе анализа корреляций фактора с исходными переменными. Например, при анализе успеваемости школьников фактор имеет высокую положительную корреляцию с оценкой по алгебре, геометрии и большую отрицательную корреляцию с оценками по рисованию, то можно предположить, что этот фактор характеризует точное мышление.
Не всегда такая интерпретация возможна. Для повышения интерпретируемости факторов добиваются большей контрастности матрицы факторных нагрузок. Метод такого улучшения результата называется методом вращения факторов. Его суть состоит в следующем. Если мы будем вращать координатные оси, образуемые факторами, мы не потеряем в точности представления данных через новые оси, и не беда, что при этом факторы не будут упорядочены по величине объясненной ими дисперсии, зато у нас появляется возможность получить более контрастные факторные нагрузки. Вращение состоит в получении новых факторов - в виде специального вида линейной комбинации имеющихся факторов:
Чтобы не вводить новые обозначения, факторы и факторные нагрузки, полученные вращением, будем обозначать теми же символами, что и до вращения. Для достижения цели интерпретируемости существует достаточно много методов, которые состоят в оптимизации подходящей функции от факторных нагрузок. Мы рассмотрим реализуемый пакетом метод VARIMAX. Этот метод состоит в максимизации "дисперсии" квадратов факторных нагрузок для переменных:
Чем сильнее разойдутся квадраты факторных нагрузок к концам отрезка [0,1], тем больше будет значение целевой функции вращения, тем четче интерпретация факторов.
В любом случае, следует иметь ввиду, что интерпретация полученных факторов в значительной степени связана с представлениями исследователя о характере изучаемого явления. По сути дела в процесс интерпретации включается большой объем информации, которая не связана с анализом собранных данных. В результате глубинное понимание смысла получаемых факторов может быть отнесено, скорее к методам качественного, а не количественного исследования.
Индивидуальные значения факторов.
Математический аппарат, используемый в факторном анализе, в действительности позволяет не вычислять непосредственно главные оси. И факторные нагрузки до и после вращения факторов и общности вычисляются за счет операций с корреляционной матрицей. Поэтому оценка значений факторов для объектов является одной из проблем факторного анализа.
Факторы, имеющие свойства полученных с помощью метода главных компонент, определяются на основе регрессионного уравнения. Известно, что для оценки регрессионных коэффициентов для стандартизованных переменных достаточно знать корреляционную матрицу переменных. Корреляционная матрица по переменным Xi и Fk определяется, исходя из модели и имеющейся матрицы корреляций Xi. Исходя из нее, регрессионным методом находятся факторы в виде линейных комбинаций исходных переменных:
Статистические гипотезы в факторном анализе
В SPSS предусмотрена проверка теста Барлетта о сферичности распределения данных. В предположении многомерной нормальности распределения здесь проверяется, не диагональна ли матрица корреляций. Если гипотеза не отвергается (наблюдаемый уровень значимости велик, скажем больше 5%) - нет смысла в факторном анализе, поскольку направления главных осей случайны. Этот тест предусмотрен в диалоговом окне факторного анализа, вместе с возможностью получения описательных статистик переменных и матрицы корреляций. На практике предположение о многомерной нормальности проверить весьма трудно, поэтому факторный анализ чаще применяется без такого анализа.
Проблема определения числа факторов.
Как уже говорилось полное описание дисперсии исходных признаков возможно только в ситуации, когда число факторов равно числу исходных признаков. Основная направленность факторного анализа – это именно сокращение числа показателей, и, следовательно, мы идем на то, что полученные факторы не будут на 100% объяснять исходную информацию и то, сколько же именно процентов будет объяснено, зависит от того, какое число факторов будет получено. Матрица объясненной дисперсии в таблице 5.1 показывает, что если будет взято 3 фактора, то они объяснят около35% исходной информации, а если возьмем 8 факторов, то такая модель объяснит уже около 68% информации. Какой процент является приемлемым, на каком числе факторов остановиться? Точного ответа на этот вопрос нет, однако есть несколько подходов, дающих определенные основания для его решения.
Первым подходом является формально-статистическим. Есть определенные математические основания говорящие, что целесообразно отбирать столько факторов, сколько существует собственных чисел корреляционной матрицы, больших единицы. Данный критерий называется критерием Кайзера. Таблица объясненной дисперсии в таблице 5.1 показывает, что для нашего примера таких чисел 5 и потому в данной модели было отобрано именно 5 факторов. Отметим, что критерий Кайзера по отбору числа факторов в команде факторного анализа SPSS используется по умолчанию.
Второй подход базируется на том, что мы сами будем отбирать число факторов, ориентируясь на то, чтобы это число факторов объясняло требуемый процент общей исходной дисперсии. Например, если исследователь решает, что факторная модель должна объяснять не менее 75% общей дисперсии исходных переменных, то таблица общей дисперсии в таблице 5.1 показывает, что необходимо взять 10 факторов.
На какой процент объясненной дисперсии необходимо ориентироваться? Не существует каких-то убедительных рекомендаций по определению этого процента, кроме одной, вполне очевидной: «Чем больше, тем лучше». В этой ситуации следует, видимо, ориентироваться на примеры предыдущих исследователей. В социологии, как правило, встречаются факторные модели, в которых объясняется 60-75% дисперсии, хотя можно примеры и с большими, и с меньшими процентами.
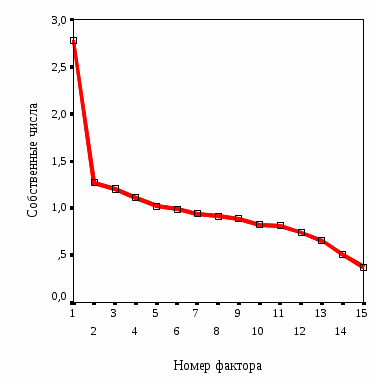
Существует еще один подход, который базируется на методе, так называемой, «каменной осыпи». Суть метода в следующем. Строится график, в котором по оси абсцисс откладываются номера факторов, а по оси ординат – значения собственных чисел, для каждого из факторов. Пример такого рода графика для модели таблицы 5.1 показан на рисунке 5.5. Как говорилось в начале, все собственные числа в методе главных компонент вычисляются в порядке убывания, поэтому график будет представлять собой понижающуюся кривую.
Далее на этом графике ищутся точки, в которых происходит более, или менее резкое понижение. В приведенном примере рисунка 5.5 можно сказать, что действительно резких понижений у нас нет. Хоть сколь-нибудь резкое понижение происходит от 9-го к 10-му фактору. Рекомендация метода «каменной осыпи» состоит в том, что надо отобрать число факторов, до момента такого рода резкого понижения. То есть в нашем примере лучше брать 9 факторов, а не 10.
Рисунок 5.5
График «каменной осыпи» для модели таблицы 5.1
Важно понимать, что ни один из изложенных подходов к определению числа факторов не дает нам доказательных оснований по отбору числа факторов. У исследователя остается большой произвол в решении этого вопроса. Основным критерием остается максимальное удобство для исследователя в построении наиболее правдоподобной модели, что, естественно, ни в каком смысле не может считаться строгим основанием.
Определение числа факторов осуществляется в меню Extraction.., вызов которого осуществляется нажатием соответствующей клавиши в главном меню команды факторного анализа (рисунок 5.1). На рисунке 5.6 показано меню Extraction. В меню Extraction так же находится окно, выбрав которое можно получить график «каменной осыпи» (окно Screenplot).
В той части меню, которая названа Extract, мы определяем, что выбор числа факторов будет осуществляться через значения собственных чисел («Eigenvalues over» - собственные числа больше чем…), либо через непосредственное указание требуемого числа факторов («Number of factors»). В любом случае мы должны указать точное значение (либо собственных чисел, либо числа факторов), которые будут основанием для отбора числа факторов в модели.
Уровень измерения переменных, используемых в факторном анализе.
Поскольку исходной информацией для метода факторного анализа является матрица коэффициентов корреляции Пирсона, то это, автоматически, диктует нам возможность использования в данном методе переменных, измеренных только по количественным (интервальным, либо абсолютным) шкалам, либо дихотомических переменных.