Статистический анализ выборочных совокупностей

После процедур первичной обработки исходная совокупность опытных результатов представляется выборочной совокупностью, для которой выполнены важнейшие требования, обеспечивающие ее репрезентативность.
Проверка гипотезы о нормальном распределении генеральной совокупности

Использование регрессионного анализа с целью прогноза опирается на гипотезу о нормальности распределения исследуемой совокупности опытных данных. Подбор вида любого из предполагаемых законов распределения рекомендуется начинать с построения гистограммы опытных значений.

Для построения гистограммы сначала нужно найти наименьшее x_min и наибольшее x_max из выборочных значений, а исходные данные x_i (i=1,2,…,n),то есть промежуток [x_min, x_max], разбить на ряд частичных интервалов. При разбиении исходного промежутка [x_min, x_max] на ряд частичных интервалов применяется следующая формула для вычисления искомой длины частичных интервалов:

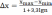
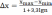(8)

Число l таких частичных интервалов в дальнейшем может быть уменьшено, если в отдельные интервалы не попадает ни одного значения (или попадает слишком мало значений).

Таблица 10 – Интервалы значений

	хmin	хmax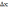
L	278200	427300	31886
m1	625,00	2540,00	410
m2	10,00	51,00	8,8
m3	15,00	65,00	10,7
N	29090,00	58420,00	62,72
Kч	2,203	6,170	0,8
Kл	0,034	0,124	0,02
Kп.з.	0,529	1,688	0,25
Kт	23,000	46,544	5,0
S	1527,60	11161,50	2060
d	17,80	33,50	3,4
e	10360,00	14383,00	860
I	11,50	71,80	12,9
V	65,50	404,80	72,6
Vp	41400,00	244700,00	43477

---

Гистограммы:


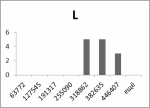
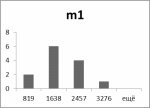
Рис.1 Рис.2



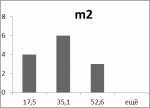
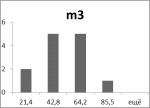
Рис.3 Рис.4


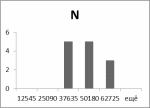
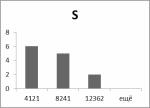
Рис.5 Рис.6


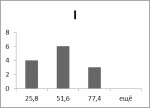
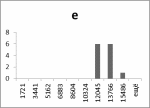
Рис.7 Рис.8



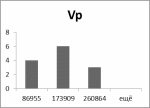
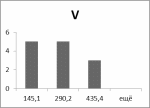
Рис.9 Рис.10


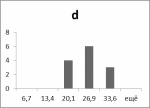
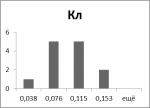
Рис.11 Рис.12



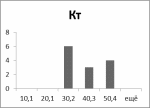
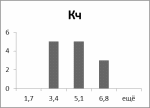
Рис.13 Рис.14


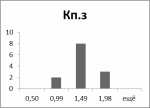
Рис. 15

Так как объем рассмотренных выборочных совокупностей невелик, можно было не выполнять проверку на нормальность их распределения.
Проверка гипотезы о значимости коэффициента корреляции

Проверку значимости коэффициента корреляции двух совокупностей опытных данных можно выполнить двумя способами: с помощью критерия Стьюдента и с помощью критерия Фишера-Снедекора.

Формула для нахождения коэффициента парной корреляции:

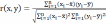
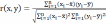(9)

Таблица 11 - Вычисленные значения коэффициентов корреляции

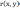	L	S	D	e	I	V	Vp
m1	0,976	-0,848	-0,890	-0,599	-0,920	-0,935	-0,948
m2	0,940	-0,835	-0,800	-0,524	-0,806	-0,836	-0,857
m3	0,874	-0,780	-0,936	-0,721	-0,968	-0,972	-0,979
N	0,899	-0,740	-0,775	-0,545	-0,772	-0,833	-0,838
Kч	0,941	-0,861	-0,930	-0,650	-0,943	-0,965	-0,977
Kл	0,873	-0,824	-0,772	-0,505	-0,745	-0,787	-0,812
Kп.з.	0,663	-0,631	-0,876	-0,776	-0,890	-0,893	-0,897
Kт	-0,865	0,838	0,923	0,613	0,933	0,931	0,937

---

1. 
   Проверка значимости коэффициента корреляции с помощью критерия Фишера-Снедекора.
   

Формула для расчета опытного значения F-критерия Фишера-Снедекора для проверки значимости коэффициента r_xy(x,y) парной линейной корреляции при заданном объеме n выборочной совокупности:

---

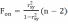
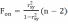(10)

Таблица 12 - Вычисленные опытные значения критерия Фишера

	L					S						D
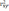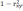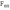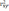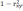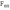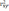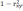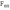m1	0,95		0,05		220,81	0,72		0,28		28,26	0,79			0,21		41,89
m2	0,88		0,12		83,94	0,70		0,30		25,25	0,64			0,36		19,49
m3	0,76		0,24		35,44	0,61		0,39		17,11	0,88			0,12		77,91
N	0,81		0,19		46,51	0,55		0,45		13,35	0,60			0,40		16,52
Kч	0,89		0,11		84,86	0,74		0,26		31,41	0,87			0,13		70,98
	L					S						D
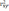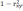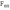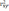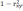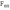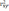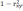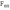Kл	0,76		0,24		35,35	0,68		0,32		23,21	0,60			0,40		16,26
Kп.з.	0,44		0,56		8,61	0,40		0,60		7,29	0,77			0,23		36,14
Kт	0,75		0,25		32,59	0,70		0,30		25,85	0,85			0,15		63,63
		E							I
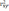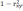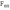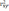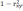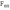m1		0,36		0,64			6,15		0,85				0,15		60,90
m2		0,27		0,73			4,15		0,65				0,35		20,41
m3		0,52		0,48			11,94		0,94				0,06		162,59
N		0,30		0,70			4,64		0,60				0,40		16,18
Kч		0,42		0,58			8,03		0,89				0,11		89,17
Kл		0,26		0,74			3,77		0,56				0,44		13,75
Kп.з		0,60		0,40			16,63		0,79				0,21		42,06
Kт		0,38		0,62			6,62		0,87				0,13		73,99
		V							Vp
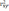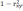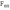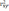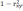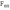m1		0,87		0,13			76,70		0,90				0,10		97,91
m2		0,70		0,30			25,53		0,73				0,27		30,44
m3		0,94		0,06			184,87		0,96				0,04		259,79
N		0,69		0,31			24,95		0,70				0,30		26,05
Kч		0,93		0,07			147,82		0,95				0,05		232,57
		V							Vp
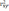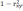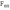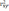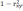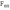Kл		0,62		0,38			17,88		0,66				0,34		21,33
Kп.з		0,80		0,20			43,20		0,80				0,20		45,22
Kт		0,87		0,13			71,84		0,88				0,12		79,02

---

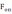
Вычисленные опытные значения 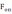сравниваются с критическим (табличным) значением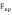 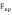=F(α;k₁;k₂) критерия Фишера-Снедекора. Критические значения критерия Фишера-Снедекора содержатся в статистических таблицах и зависят:

- от выбранного уровня значимости α;

- от показателей k₁ и k₂ степеней свободы критерия F.

В рассматриваемом случае парной линейной корреляции k₁=m-2, k₂=1, то есть

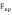
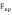=F(α;k₁;k₂)= F(α;m-2;1)

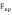
Для данного случая k₁=11, k₂=1 при уровне значимости α=0,05 и критическое значение критерия Фишера-Снедекора 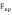=4,84.

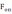
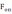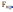
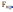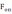
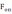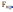
Если выполняется неравенство > , то с вероятностью α=0,05 будет неверно отвергать гипотезу о значимости коэффициента парной линейной корреляции. Если < 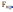, делается вывод о том, что с вероятностью p=1-α=1-0,05=0,95 исследуемая корреляционная связь случайных величин незначима и ею можно пренебречь.

Проанализировав полученные критерии Фишера, следующие корреляционные взаимосвязи можно считать незначимыми, так как не удовлетворяют неравенству > ,:

---

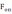
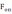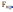
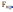Смотрите также файлы

• Влияние физической культуры и спорта на организм человека.rtf

• 1 хаттамасы маусым 2023ж саат минуттан саат минута дейін Абдрашид Ділшат лы 1304000Есептеу техникасы жне бадарламамен амтасыз ету.docx

• Организационная структура и взаимодействие подразделений организации с бухгалтерией (кассой).docx

• Организационное обеспечение (ОО).docx

• Теоретические основы организации рекламной деятельности в туристическом бизнесе.docx