Файл: Разработка алгоритма и математической модели отсеивание грубых погрешностей измерений и оценка их достоверности.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 25.10.2023
Просмотров: 149
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
можно ошибаться, т.е. на сколько процентов отвергается гипотеза. Тогда величина P=1-α является доверительной вероятностью (надежностью).
Уровень значимости – мера наших требований к ответу: чем больших гарантий мы будем требовать, тем менее определенным станет ответ. Ответ одновременно очень точный и очень надежный, как правило, стоит очень дорого. Опыт использования статистики в разнообразных ситуациях в течение нескольких десятилетий показал, что обычно в практических ситуациях определяющим значением α является 0,05. Такое значение, называемое иногда 5%-ным уровнем риска, соответствует вероятности верного ответа, т.е. его надежности при проверке гипотез P=1-0,05=0,95 или 95%. При этом говорят, что в среднем только в 5 случаев из 100 возможна ошибка. Конечно, никогда нельзя дать 100%-й гарантии. Подобное желание приводит к необходимости выполнять бесконечное много опытов, что абсурдно.
Поскольку проверка гипотез ведется при ограниченной информации (по выбо
рке), то могут возникнуть ошибки двух родов. Если будет отвергнута правильная гипотеза, то совершается ошибка первого рода, если будет допущена неправильная гипотеза, то совершается ошибка второго рода. Очевидно, что вероятность допустить ошибку первого рода, равна . Область, отвечающая вероятности α, называется критической, а дополняющая ее область, вероятность попадания в которую P(Oα)=1-α, называется допустимой.
Общий подход решения задач при использовании статистических гипотез состоит в проверке нулевой гипотезы Н0, т.е. об отсутствии различия между теоретическими и экспериментальными результатами, разброс которых объясняется случайными факторами. Проверка гипотезы – это правило, по которому она принимается или отвергается.
Чаще всего в инженерной практике изначально зада-ются критическим значением уровня значимости α или доверительной вероятности P=1-α.
2.3. Отсевгрубыхпогрешностей
В литературе можно встретить большое количество различных рекомендаций для проведения отсева грубых погрешностей наблюдений. Наиболее распространенным и теоретически обоснованным является метод
, основанный на доверительной вероятности.
Было установлено, что при нормальном законе распределения случайная величина не должна отличаться от своего математического ожидания с веро-ятностями: 90% на 1,64 bx; 95% на 1,96 bx и т.п. Но это теоретические расчеты, в предположении, что известно математическое ожидание Мx, дисперсия bx, а результаты измерений строго подчиняются нормальному закону распределения при числе испытаний n--N. Таким образом, в случае нормального закона распределения, при достаточно большом числе наблюдений (как показывает
п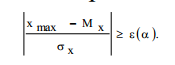
рактический опыт, более 30), если какое-либо из измеренных значений xmax отличается от его математического ожидания более чем на 1,96 bx, то с вероятностью 95% его можно отбросить. Следовательно, условие, что изме-ренная величина Xmax является грубой погрешностью можно выразить соотношением
На практике, как правило, число измерений конечно и в большинстве случаев не превышает 15–30. При таком малом числе наблюдений мы можем определить только оценки математического ожидания Мx и дисперсии bx,
т.е. рассчитать x и Sx. Измерения при малом числе наблюдений чаще всего дают меньшее значение средне-квадратичной погрешности Sx по сравнению с погрешностью для достаточно большого ряда тех же измерений (в
пределе всей генеральной совокупности) bx. Поэтому при неизвестных действительных значениях Мx, bx, ограниченном числе испытаний, используют распределение Стьюдента и довольствуются весьма приближенными методами. Стьюдент – псевдоним У.С. Госсета (1876-1937) –химика, работавшего в одной из пивоварен фирм Великобритании. Он почти самостоятельно разработал статистику малых выборок. Поскольку в современной
технике чаще всего исследуются небольшие по объему выборки (менее 30), то работа Стьюдента имеет большое практическое значение.
Процедура отсева грубых погрешностей измерений заключается в следующем:
1. По результатам наблюдений (измерений) и объему выборки n рассчитываются оценки математического ожидания x и дисперсии Sx;
2 Из всего ряда наблюдений выбирается наблюдение (измерение), имеющее наибольшее отклонение от среднеарифметического значения Хmax;
3. Формулируется нуль-гипотеза Н0: отклонение Хmax от Х несущественно с доверительной вероятностью Р (уровнем значимости α).
4. Для оценки этой гипотезы рассчитывается максимальное относительное (по отношению к среднеквадратичному) отклонение:
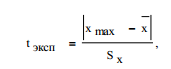
где Хmax – "выскакивающее" значение.
5. В качестве критерия проверки статистической нуль-гипотезы используется теоретическое значение критерия Стьюдента t, которое зависит от уровня значимости α или доверительной вероятности P=1-α.
tα,m=n-1 – представляет собой допустимое отклонение случайной величины, выраженное в долях оценки среднеквадратичного отклонения, и учитывает ограниченность объема выборки (n) и заданную доверительную вероятность (P).
6. Если tэксп>tα,m, то имеется достаточно основания с вероятностью P исключить "выскакивающее" значение как грубую ошибку и отвергнуть нуль-гипотезу. В противном случае tэксп
2.4. Определение доверительныхинтерваловдля исследуемыхвеличин
Уровень значимости – мера наших требований к ответу: чем больших гарантий мы будем требовать, тем менее определенным станет ответ. Ответ одновременно очень точный и очень надежный, как правило, стоит очень дорого. Опыт использования статистики в разнообразных ситуациях в течение нескольких десятилетий показал, что обычно в практических ситуациях определяющим значением α является 0,05. Такое значение, называемое иногда 5%-ным уровнем риска, соответствует вероятности верного ответа, т.е. его надежности при проверке гипотез P=1-0,05=0,95 или 95%. При этом говорят, что в среднем только в 5 случаев из 100 возможна ошибка. Конечно, никогда нельзя дать 100%-й гарантии. Подобное желание приводит к необходимости выполнять бесконечное много опытов, что абсурдно.
Поскольку проверка гипотез ведется при ограниченной информации (по выбо
рке), то могут возникнуть ошибки двух родов. Если будет отвергнута правильная гипотеза, то совершается ошибка первого рода, если будет допущена неправильная гипотеза, то совершается ошибка второго рода. Очевидно, что вероятность допустить ошибку первого рода, равна . Область, отвечающая вероятности α, называется критической, а дополняющая ее область, вероятность попадания в которую P(Oα)=1-α, называется допустимой.
Общий подход решения задач при использовании статистических гипотез состоит в проверке нулевой гипотезы Н0, т.е. об отсутствии различия между теоретическими и экспериментальными результатами, разброс которых объясняется случайными факторами. Проверка гипотезы – это правило, по которому она принимается или отвергается.
Чаще всего в инженерной практике изначально зада-ются критическим значением уровня значимости α или доверительной вероятности P=1-α.
2.3. Отсевгрубыхпогрешностей
В литературе можно встретить большое количество различных рекомендаций для проведения отсева грубых погрешностей наблюдений. Наиболее распространенным и теоретически обоснованным является метод
, основанный на доверительной вероятности.
Было установлено, что при нормальном законе распределения случайная величина не должна отличаться от своего математического ожидания с веро-ятностями: 90% на 1,64 bx; 95% на 1,96 bx и т.п. Но это теоретические расчеты, в предположении, что известно математическое ожидание Мx, дисперсия bx, а результаты измерений строго подчиняются нормальному закону распределения при числе испытаний n--N. Таким образом, в случае нормального закона распределения, при достаточно большом числе наблюдений (как показывает
п
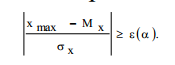рактический опыт, более 30), если какое-либо из измеренных значений xmax отличается от его математического ожидания более чем на 1,96 bx, то с вероятностью 95% его можно отбросить. Следовательно, условие, что изме-ренная величина Xmax является грубой погрешностью можно выразить соотношением На практике, как правило, число измерений конечно и в большинстве случаев не превышает 15–30. При таком малом числе наблюдений мы можем определить только оценки математического ожидания Мx и дисперсии bx,
т.е. рассчитать x и Sx. Измерения при малом числе наблюдений чаще всего дают меньшее значение средне-квадратичной погрешности Sx по сравнению с погрешностью для достаточно большого ряда тех же измерений (в
пределе всей генеральной совокупности) bx. Поэтому при неизвестных действительных значениях Мx, bx, ограниченном числе испытаний, используют распределение Стьюдента и довольствуются весьма приближенными методами. Стьюдент – псевдоним У.С. Госсета (1876-1937) –химика, работавшего в одной из пивоварен фирм Великобритании. Он почти самостоятельно разработал статистику малых выборок. Поскольку в современной
технике чаще всего исследуются небольшие по объему выборки (менее 30), то работа Стьюдента имеет большое практическое значение.
Процедура отсева грубых погрешностей измерений заключается в следующем:
1. По результатам наблюдений (измерений) и объему выборки n рассчитываются оценки математического ожидания x и дисперсии Sx;
2 Из всего ряда наблюдений выбирается наблюдение (измерение), имеющее наибольшее отклонение от среднеарифметического значения Хmax;
3. Формулируется нуль-гипотеза Н0: отклонение Хmax от Х несущественно с доверительной вероятностью Р (уровнем значимости α).
4. Для оценки этой гипотезы рассчитывается максимальное относительное (по отношению к среднеквадратичному) отклонение:
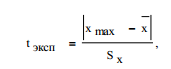
где Хmax – "выскакивающее" значение.
5. В качестве критерия проверки статистической нуль-гипотезы используется теоретическое значение критерия Стьюдента t, которое зависит от уровня значимости α или доверительной вероятности P=1-α.
tα,m=n-1 – представляет собой допустимое отклонение случайной величины, выраженное в долях оценки среднеквадратичного отклонения, и учитывает ограниченность объема выборки (n) и заданную доверительную вероятность (P).
6. Если tэксп>tα,m, то имеется достаточно основания с вероятностью P исключить "выскакивающее" значение как грубую ошибку и отвергнуть нуль-гипотезу. В противном случае tэксп
2.4. Определение доверительныхинтерваловдля исследуемыхвеличин