Файл: Разработка алгоритма и математической модели отсеивание грубых погрешностей измерений и оценка их достоверности.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 25.10.2023
Просмотров: 148
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
, x2,..., xn, в той или иной степени отражающая действительное значение параметра O.
Если говорить о характеристиках распределений вероятностей, то характеристики теоретических распределений (Mx, bx2, Mo, Me) можно рассматривать как характеристики, существующие в генеральной совокупности, а характеризующие эмпирическое распределение – как выборочные их характеристики (оценки). Числовые параметры для оценки Mx, bx2 и др. – называются иногда статистиками.
Для оценки математического ожидания используется среднеарифметическое (среднее значение) ряда измерений по выборке:
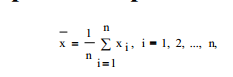(2.1)
где хi– реализация либо дискретной, либо отдельная точка для непрерывной случайной величины; n – объем выборки.
Для характеристики разброса случайной величины используется оценка теоретической дисперсии – выборочные дисперсии ( рис.2.1):
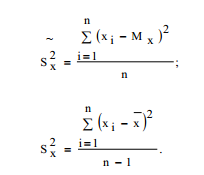
(2.2а)
(2.2б)
Н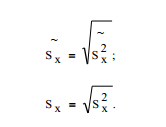
еотрицательное значение квадратного корня
из выборочной дисперсии – это выборочное стандартное отклонение (выборочное среднеквадратичное) отклонение
(3.3а)
(3.3б)
Следует отметить, что в любой задаче, связанной с выполнением измерений, возможны два способа получения оценки значения bx2.
При использовании первого способа снимается последовательность показаний прибора и путем сравнения полученных результатов с известным или калиброванным значением измеряемой величины находится после-довательность отклонений. Затем полученная последовательность отклонений используется для вычисления среднего квадратичного отклонения по формуле (3.3а).
Второй способ получения оценки значения bx2 состоит в определении среднего арифметического x, т.к. в этом случае действительное (точное) значение измеряемой величины неизвестно. В этом случае целесообразно использовать другую, формулу для нахождения средне-квадратичного отклонения (3.2б, 3.3б). Деление на (n-1) производится по той причине, что наилучшая оценка, получаемая путем усреднения массива Х, будет отли-чаться от точного значения на некоторую величину, если рассматривается
выборка, а не вся генеральная совокупность. В этом случае сумма квадратов отклонений будет несколько меньше, чем при использовании истинного среднего. При делении на (n-1) вместо n эта погрешность будет частично скорректирована. В некоторых руководствах по математической статистике рекомендуется при вычислении выборочного средне-квадратичного отклонения всегда делить на (n-1), хотя иногда этого делать не следует. Нужно делить на (n-1) лишь в тех случаях, когда истинное значение не было получено независимым способом.
Выборочное значение коэффициента вариации V, являющееся мерой относительной изменчивости случайной величины, вычисляют по формуле
V=Sx/x (3.4а)
или в процентах
V=Sx/x *100 %. (3.4б)
Та из выборок имеет большее рассеяние, у которой вариация больше.
2.2. Статистическиегипотезы
Как уже отмечалось, в ходе предварительной обработки экспериментальных данных решаются следующие задачи:
- отсев грубых ошибок (промахов) наблюдений;
- доверительная оценка измеряемых величин;
- проверка соответствия распределения результатов измерений закону нормального распределения.
Проверка и решение этих задач осуществляется с помощью статистических гипотез. Статистическими гипотезами (Н) называются предположения о свойствах генеральной совокупности, т.е. относительно закона распределения (f(x), F(x)) и их параметров (Мx, bx2 и др.).
Таким образом, основная выдвинутая гипотеза является нульгипотезой Н0. Весьма часто она формулируется о том, что оценки Oa* и Ob* полученные для выборок А и В, принадлежат к одной генеральной совокупности, т.е. разница между Oa* и Ob* фактически равна нулю и возникла в силу случайности отбора элементов и ограниченности объема выборки. Противоречащие ей гипотезы Нi называются альтернативными, или конкурирующими.
Правильность этих гипотез проверяется путем вычисления некоторых числовых характеристик по данным наблюдений (измерений) и сравнения их с теми, которые должны быть при условии, что проверяемая гипотеза истинна, а наблюдаемые отклонения объясняются слу
чайными колебаниями в выборках и их ограниченностью. Такие характеристики называют критериями проверки статистических гипотез Gr. Для этого строится случайная величина – степень рассогласования теорети-ческого и экспериментального распределения. По величине рассогласования можно проверить является ли это расхождение незначительным или существенным. Если Grэксп и Grтеор отличаются существенно, то гипотеза от-вергается, если мало, то гипотеза принимается.
Таким образом, статистические гипотезы носят вероятностный характер. Это говорит о том, что в ряде случаев можно ошибиться. Для количественной характеристики степени ошибки используется показатель α, который называется уровнем значимости. Произведение α 100% показывает в скольких случаях из 100
Если говорить о характеристиках распределений вероятностей, то характеристики теоретических распределений (Mx, bx2, Mo, Me) можно рассматривать как характеристики, существующие в генеральной совокупности, а характеризующие эмпирическое распределение – как выборочные их характеристики (оценки). Числовые параметры для оценки Mx, bx2 и др. – называются иногда статистиками.
Для оценки математического ожидания используется среднеарифметическое (среднее значение) ряда измерений по выборке:
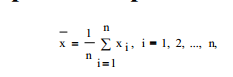(2.1)где хi– реализация либо дискретной, либо отдельная точка для непрерывной случайной величины; n – объем выборки.
Для характеристики разброса случайной величины используется оценка теоретической дисперсии – выборочные дисперсии ( рис.2.1):
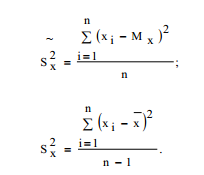
(2.2а)
(2.2б)
Н
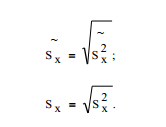еотрицательное значение квадратного корня
из выборочной дисперсии – это выборочное стандартное отклонение (выборочное среднеквадратичное) отклонение
(3.3а)
(3.3б)
Следует отметить, что в любой задаче, связанной с выполнением измерений, возможны два способа получения оценки значения bx2.
При использовании первого способа снимается последовательность показаний прибора и путем сравнения полученных результатов с известным или калиброванным значением измеряемой величины находится после-довательность отклонений. Затем полученная последовательность отклонений используется для вычисления среднего квадратичного отклонения по формуле (3.3а).
Второй способ получения оценки значения bx2 состоит в определении среднего арифметического x, т.к. в этом случае действительное (точное) значение измеряемой величины неизвестно. В этом случае целесообразно использовать другую, формулу для нахождения средне-квадратичного отклонения (3.2б, 3.3б). Деление на (n-1) производится по той причине, что наилучшая оценка, получаемая путем усреднения массива Х, будет отли-чаться от точного значения на некоторую величину, если рассматривается
выборка, а не вся генеральная совокупность. В этом случае сумма квадратов отклонений будет несколько меньше, чем при использовании истинного среднего. При делении на (n-1) вместо n эта погрешность будет частично скорректирована. В некоторых руководствах по математической статистике рекомендуется при вычислении выборочного средне-квадратичного отклонения всегда делить на (n-1), хотя иногда этого делать не следует. Нужно делить на (n-1) лишь в тех случаях, когда истинное значение не было получено независимым способом.
Выборочное значение коэффициента вариации V, являющееся мерой относительной изменчивости случайной величины, вычисляют по формуле
V=Sx/x (3.4а)
или в процентах
V=Sx/x *100 %. (3.4б)
Та из выборок имеет большее рассеяние, у которой вариация больше.
2.2. Статистическиегипотезы
Как уже отмечалось, в ходе предварительной обработки экспериментальных данных решаются следующие задачи:
- отсев грубых ошибок (промахов) наблюдений;
- доверительная оценка измеряемых величин;
- проверка соответствия распределения результатов измерений закону нормального распределения.
Проверка и решение этих задач осуществляется с помощью статистических гипотез. Статистическими гипотезами (Н) называются предположения о свойствах генеральной совокупности, т.е. относительно закона распределения (f(x), F(x)) и их параметров (Мx, bx2 и др.).
Таким образом, основная выдвинутая гипотеза является нульгипотезой Н0. Весьма часто она формулируется о том, что оценки Oa* и Ob* полученные для выборок А и В, принадлежат к одной генеральной совокупности, т.е. разница между Oa* и Ob* фактически равна нулю и возникла в силу случайности отбора элементов и ограниченности объема выборки. Противоречащие ей гипотезы Нi называются альтернативными, или конкурирующими.
Правильность этих гипотез проверяется путем вычисления некоторых числовых характеристик по данным наблюдений (измерений) и сравнения их с теми, которые должны быть при условии, что проверяемая гипотеза истинна, а наблюдаемые отклонения объясняются слу
чайными колебаниями в выборках и их ограниченностью. Такие характеристики называют критериями проверки статистических гипотез Gr. Для этого строится случайная величина – степень рассогласования теорети-ческого и экспериментального распределения. По величине рассогласования можно проверить является ли это расхождение незначительным или существенным. Если Grэксп и Grтеор отличаются существенно, то гипотеза от-вергается, если мало, то гипотеза принимается.
Таким образом, статистические гипотезы носят вероятностный характер. Это говорит о том, что в ряде случаев можно ошибиться. Для количественной характеристики степени ошибки используется показатель α, который называется уровнем значимости. Произведение α 100% показывает в скольких случаях из 100