Файл: Разработка алгоритма и математической модели отсеивание грубых погрешностей измерений и оценка их достоверности.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 25.10.2023
Просмотров: 147
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
ля решения вопроса, является это промахом или нет и можно ли исключить выявленные промахи, используют статистические критерии:
- предварительно проверяют, какому виду распределения соответствует распределение результатов измерений. Если результаты принадлежат к нормальному распределению, то результат измерения можно считать промахом в случае, когда
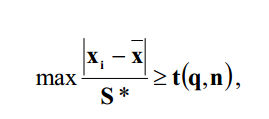 (1.5)
(1.5)
где S* – среднеквадратическое отклонение результатов наблюдений; хi – результат каждого измерения;
x – среднее арифметическое значение группы результатов измерений; t(q, n) – квантиль распределения, зависящий от уровня значимости q и
количества наблюдений n в группе.
Обнаруженные и вычисленные систематические погрешности измерения вносят в результаты измерений в виде поправок или поправочных множителей,
таким образом исключая их, а неисключенные систематические и случайные погрешности составляют погрешность результата измерения.
ВЫВОДЫ ПО 1 ГЛАВЕ
Результаты измерений в зависимости от цели измерительной задачи могут быть представлены числом, в виде таблицы, графика или в другом виде.
Формы представл
ения результатов измерений и их погрешностей должны соответствовать МИ 1317-86.
Погрешность результата измерений, как правило, выражают одной значащей цифрой (МИ 2091-90). Две значащие цифры сохраняют:
- при точных измерениях;
- если первая значащая цифра не более трех;
- если предел допускаемой погрешности задан двумя значащими цифрами.
2. ГЛАВА. ПРЕДВАРИТЕЛЬНАЯ ОБРАБОТКА ЭКСПЕ-РИМЕНТАЛЬНЫХ ДАННЫХ
Предварительная обработка результатов измерений и наблюдений необходима для того, чтобы в дальнейшем с наибольшей эффективностью, а главное корректно, использовать для построения эмпирических зависимостей статистические методы и корректно проанализировать полученные результаты.
Содержание предварительной обработки состоит в отсеивании грубых погрешностей, оценке достоверности результатов измерений. Другим важным моме
нтом предварительной обработки данных является проверка соответствия распределения результатов измерения закону нормального распределения и определения параметров распределения. Если эта гипотеза неприемлема, то следует определить какому закону распределения подчиняются опытные данные и, если это возможно, преобразовать данное распределение к нормальному.
2.1. Вычисление характеристикэмпирическихраспределений
П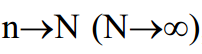 ри рассмотрении основных положений теории вероятностей и математической статистики, определении параметров распределения мы исходили из предположения, что осуществляется достаточно большое, в пределе бесконечное число испытаний что практически осуществить невозможно. Однако имеются методы, которые позволяют оценить эти параметры по выборке (части) случайных событий.
ри рассмотрении основных положений теории вероятностей и математической статистики, определении параметров распределения мы исходили из предположения, что осуществляется достаточно большое, в пределе бесконечное число испытаний что практически осуществить невозможно. Однако имеются методы, которые позволяют оценить эти параметры по выборке (части) случайных событий.
Г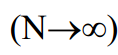
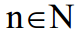 енеральной называется совокупность всех мыслимых значений наблюдений, которые мы могли бы сделать при данном комплексе условий. Другими словами все возмо
енеральной называется совокупность всех мыслимых значений наблюдений, которые мы могли бы сделать при данном комплексе условий. Другими словами все возмо
жные реализации случайной величины, теоре-тически в пределе их может быть бесконечное число . Часть этой совокупности, т.е. результаты ограниченного ряда наблюдений x1,x2,...,xn случайной величины, можно рассматривать как выборочное значение случайной величины (например, при определении химического состава сплавов, их механической прочности и т.п.). Если все слитки данной марки стали, чугуна, сплава разделать на образцы и исследовать их химический состав, механическую прочность и другие физические характеристики, то имели бы генеральную совокупность наблюдений. Фактически доступно, возможно (целесообразно), исследовать свойства весьма ограниченного числа образцов – это и есть выборка их генеральной совокупности. По результатам такого ограниченного числа наблюдений можно определить точечные оценки законов рас-пределения и их параметров. Оценкой (или выборочной статистикой) O* какого-либо параметра O называется произвольная функция O*= O* (x1, x2,..., xn) наблюдаемых значений x1
- предварительно проверяют, какому виду распределения соответствует распределение результатов измерений. Если результаты принадлежат к нормальному распределению, то результат измерения можно считать промахом в случае, когда
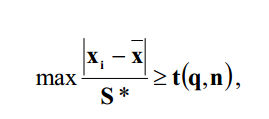 (1.5)
(1.5)где S* – среднеквадратическое отклонение результатов наблюдений; хi – результат каждого измерения;
x – среднее арифметическое значение группы результатов измерений; t(q, n) – квантиль распределения, зависящий от уровня значимости q и
количества наблюдений n в группе.
Обнаруженные и вычисленные систематические погрешности измерения вносят в результаты измерений в виде поправок или поправочных множителей,
таким образом исключая их, а неисключенные систематические и случайные погрешности составляют погрешность результата измерения.
ВЫВОДЫ ПО 1 ГЛАВЕ
Результаты измерений в зависимости от цели измерительной задачи могут быть представлены числом, в виде таблицы, графика или в другом виде.
Формы представл
ения результатов измерений и их погрешностей должны соответствовать МИ 1317-86.
Погрешность результата измерений, как правило, выражают одной значащей цифрой (МИ 2091-90). Две значащие цифры сохраняют:
- при точных измерениях;
- если первая значащая цифра не более трех;
- если предел допускаемой погрешности задан двумя значащими цифрами.
2. ГЛАВА. ПРЕДВАРИТЕЛЬНАЯ ОБРАБОТКА ЭКСПЕ-РИМЕНТАЛЬНЫХ ДАННЫХ
Предварительная обработка результатов измерений и наблюдений необходима для того, чтобы в дальнейшем с наибольшей эффективностью, а главное корректно, использовать для построения эмпирических зависимостей статистические методы и корректно проанализировать полученные результаты.
Содержание предварительной обработки состоит в отсеивании грубых погрешностей, оценке достоверности результатов измерений. Другим важным моме
нтом предварительной обработки данных является проверка соответствия распределения результатов измерения закону нормального распределения и определения параметров распределения. Если эта гипотеза неприемлема, то следует определить какому закону распределения подчиняются опытные данные и, если это возможно, преобразовать данное распределение к нормальному.
2.1. Вычисление характеристикэмпирическихраспределений
П
Г
жные реализации случайной величины, теоре-тически в пределе их может быть бесконечное число . Часть этой совокупности, т.е. результаты ограниченного ряда наблюдений x1,x2,...,xn случайной величины, можно рассматривать как выборочное значение случайной величины (например, при определении химического состава сплавов, их механической прочности и т.п.). Если все слитки данной марки стали, чугуна, сплава разделать на образцы и исследовать их химический состав, механическую прочность и другие физические характеристики, то имели бы генеральную совокупность наблюдений. Фактически доступно, возможно (целесообразно), исследовать свойства весьма ограниченного числа образцов – это и есть выборка их генеральной совокупности. По результатам такого ограниченного числа наблюдений можно определить точечные оценки законов рас-пределения и их параметров. Оценкой (или выборочной статистикой) O* какого-либо параметра O называется произвольная функция O*= O* (x1, x2,..., xn) наблюдаемых значений x1