Файл: Урок алгебры в 11 классе по теме Предел функции в точке. Производная функции в точке. Геометрический и физический смысл производной..doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 25.10.2023
Просмотров: 109
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Урок алгебры в 11 классе по теме «Предел функции в точке. Производная функции в точке. Геометрический и физический смысл производной.»
Цель урока:
-
Формирование у учащихся наглядно – интуитивных представлений о пределе функции в точке. -
Развитие внимания, памяти, логического мышления; -
Воспитание старательности, организованности.
Ход урока.
1. Организационный момент.
- Здравствуйте, ребята. Тема нашего урока: «Предел функции в точке». Сегодня на уроке мы познакомимся с понятиями «предел функции в точке», «непрерывность функции», а также рассмотрим правила вычисления предела функции в точке.
2. Мотивация изучения темы.
- Эта тема очень важна для дальнейшего изучения алгебры: понятие предела функции имеет большое значение для построения графиков функций. Кроме того, в дальнейшем мы будем изучать понятие производной и без знания предела функции рассмотрение этого понятия невозможно.
3. Актуализация опорных знаний.
- Перед тем как начать изучать новую тему выполним следующее задание: постройте график функции
а) при х = 4 значение функции не существует; (рис.1)
б) при х = 4 значение функции равно 3; (рис.2)
в) при х = 4 значение функции равно 2. (рис.3)
(В ходе выполнения этого упражнения учащиеся повторяют нахождение области определения функции, а также построение графика функции, которая при данном значении аргумента либо имеет значение, либо не определена).
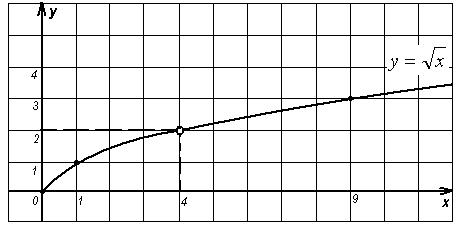
Рисунок 1
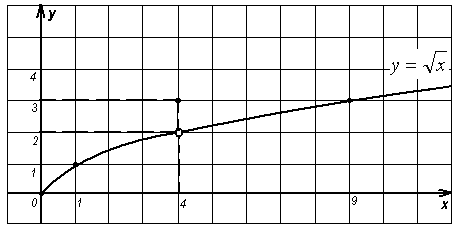
Рисунок 1
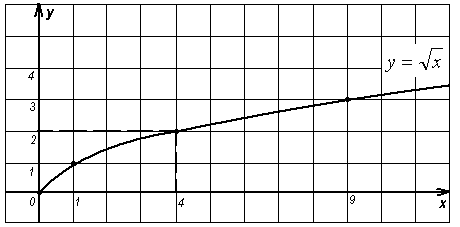
Рисунок 2
4. Изучение нового материала.
1. Предел функции в точке.
- Воспользуемся построенными графиками функций. Во всех трех случаях изображена одна и та же кривая, тем не менее, это три разные функции.
- Чем они отличаются друг от друга?
(Они отличаются друг от друга своим поведением в точке х = 4).
- Как ведет себя функция в точке х = 4 на первом графике?
(Для функции
- Как ведет себя функция в точке х = 4 на втором графике?
(Для функции
- Как ведет себя функция в точке х = 4 на третьем графике?
(Для функции
- Если мы исключим точку х = 4 из рассмотрения, то все три функции будут тождественными.
- Для всех трех случаев используется одна и та же запись:
- В общем случае эта запись выглядит следующим образом:
- Эту запись читаем так: «предел функции y=f(x) при стремлении х к а равен b».
- А теперь ответьте на такой вопрос: какую из трех рассмотренных функций естественно считать непрерывной в точке х = 4?
(Непрерывной будет третья функция)
- Так как эта функция непрерывна, то она удовлетворяет условию
- Иными словами, функцию y = f (x) называют непрерывной в точке х = а, если предел функции y = f (x) при стремлении х к а равен значению функции в точке х = а.
- Функция y = f (x) называется непрерывной на промежутке Х, если она непрерывна в каждой точке промежутка.
- При изучении различных функций (линейной, квадратичной, степенной, иррациональной, тригонометрических) мы отмечали, что они являются непрерывными либо на всей числовой прямой, либо на промежутке. Исходя из этого, можно сформулировать следующее утверждение: если выражение f (x) составлено из рациональных, иррациональных, тригонометрических выражений, то функция y
= f (x) непрерывна в любой точке, в которой определено выражение f (x).
Решение задач на закрепление понятия предела.
- Для закрепления понятия предела функции в точке рассмотрим несколько примеров на вычисление пределов функций.
Пример 1. Вычислить:
Решение. Выражение х3 – 2х2 + 5х + 3 определено в любой точке х, в частности, в точке х = 1. Следовательно, функция у = х3 – 2х2 + 5х + 3 непрерывна в точке х = 1, а потому предел функции при стремлении х к 1 равен значению функции в точке х = 1.
Имеем:
Ответ: 7.
- Для решения следующего примера нам потребуются правила вычисления предела функции в точке.
Правило 1.
Правило 2.
Правило 3.
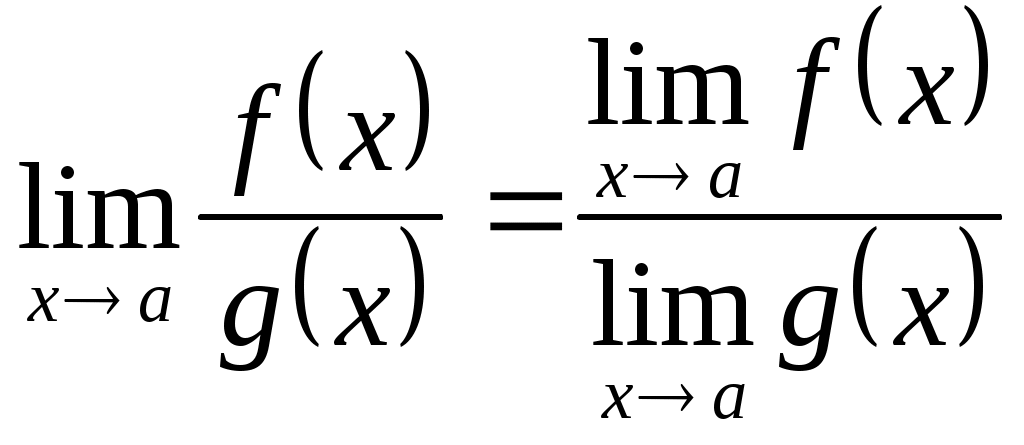 .
.Пример 2. Используя эти правила, вычислим
Решение. Выражение
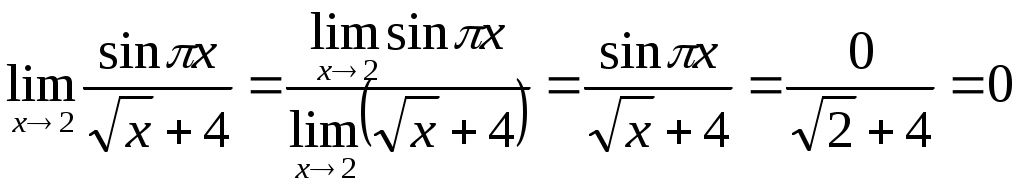 .
.Ответ: 0.
Вычислите: а)
б)
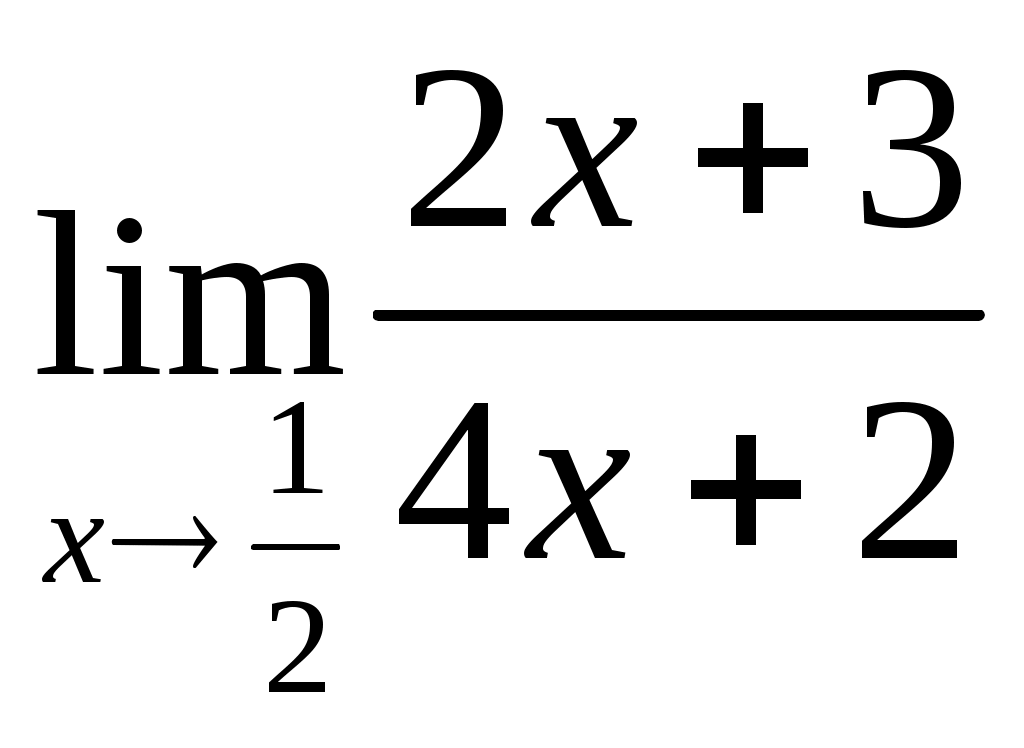 ;
;в)
г)
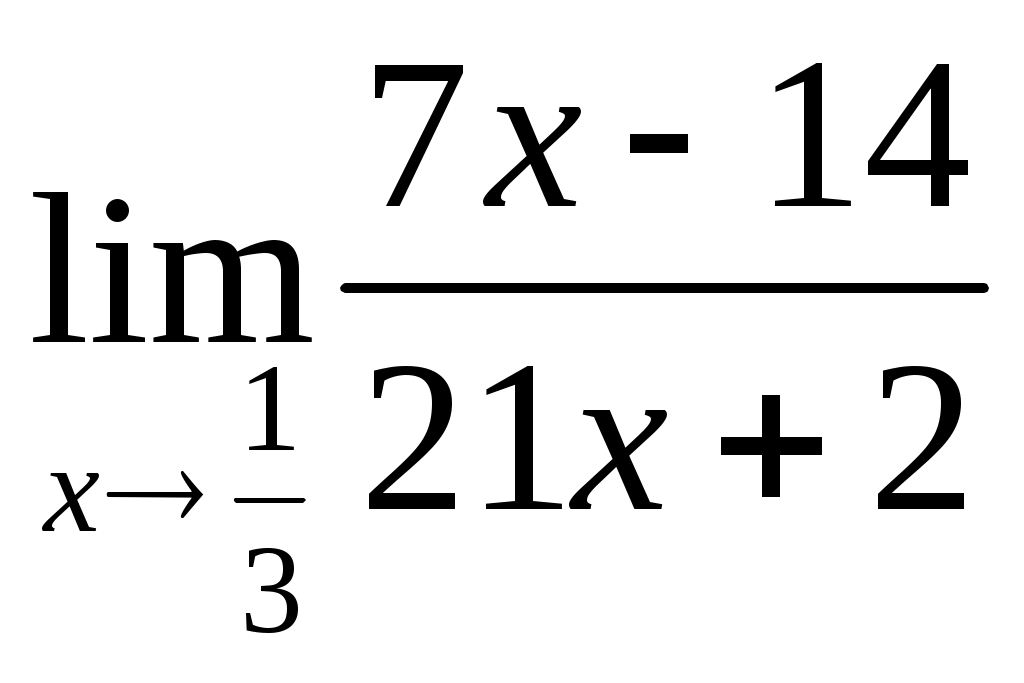 .
.Решение.
а)
х = 1. Следовательно, функция у = х2 – 3х + 5 непрерывна в точке х = 1, а потому предел функции при стремлении х к 1 равен значению функции в точке х = 1.
Имеем:
Ответ: 3.
б)
 . Выражение
. Выражение 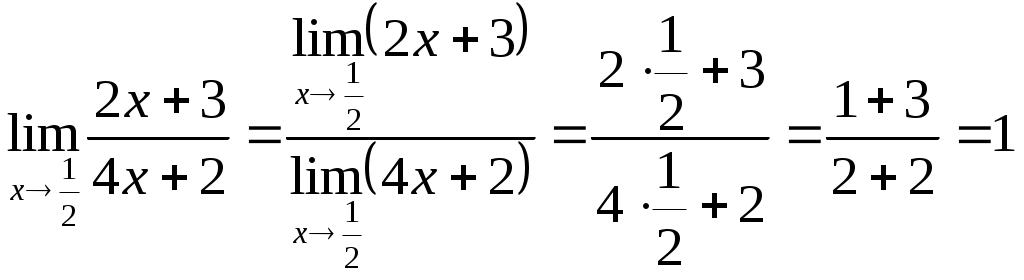 .
.Ответ: 0.
в)
Имеем:
Ответ: - 1.
г)
 . Выражение
. Выражение равен значению функции в точке х =
Имеем:
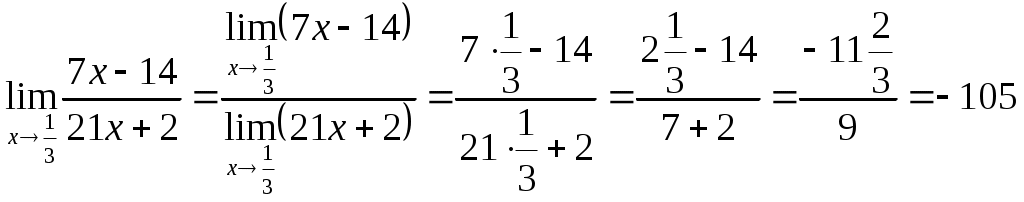 .
.- Вы заметили, что в рассмотренных примерах вычисление пределов не составило значительных сложностей: достаточно было найти значение функции в точке, к которой стремится аргумент х. Но часты случаи, когда этот прием не срабатывает.
Пример 3. Вычислить
Решение. Если подставить значение х = - 3 в заданное выражение, то и в числителе, и в знаменателе получится 0, а на нуль делить нельзя. Но заданную алгебраическую дробь можно сократить:
Значит, функции
Ответ: - 1,5.
Зарядка для глаз.
2. Задачи, приводящие к понятию производной.
Задача о скорости движения.
Рассмотрим прямолинейное движение некоторого тела. Закон движения задан формулой S = S(t), т.е. каждому моменту времени t соответствует определённое значение пройденного пути S. Найти скорость движения тела в момент времени t.
Р
 ешение: Пусть в момент времени t тело находится в точке М.
ешение: Пусть в момент времени t тело находится в точке М. Дадим аргументу t приращение Δt, за это время тело переместится в некоторую точку Р, т.е. пройдёт путь ΔS.
Итак, за время Δt тело прошло путь ΔS.
Что можно найти, зная эти два значения?
Определение: Средней скоростью движения тела называется отношение пройденного пути ко времени, в течение которого этот путь пройден.