Теорема 3. Производную частного двух дифференцируемых функций можно найти по формуле:

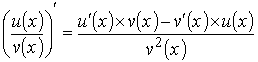, где

Доказательство (доказательство проводится совместно учителем и учениками) :

Есть функции u(x) и v(x); и

Нужно доказать, что .

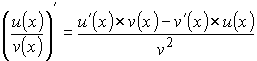Пусть .

Умножим обе части равенства на v(x) и найдем производную от обеих частей равенства.

Получим или .

Но . Тогда

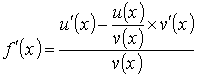или .

Мы доказали, что .

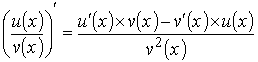Задача 3: Найти производную функции

Решение:

;

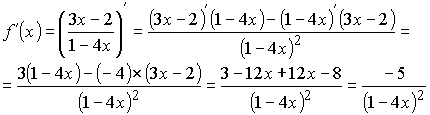Задача 4: Доказать, что

Доказательство:



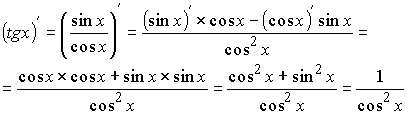
Задача 5: Доказать, что (самостоятельно)

Рассмотреть таблицу производных.



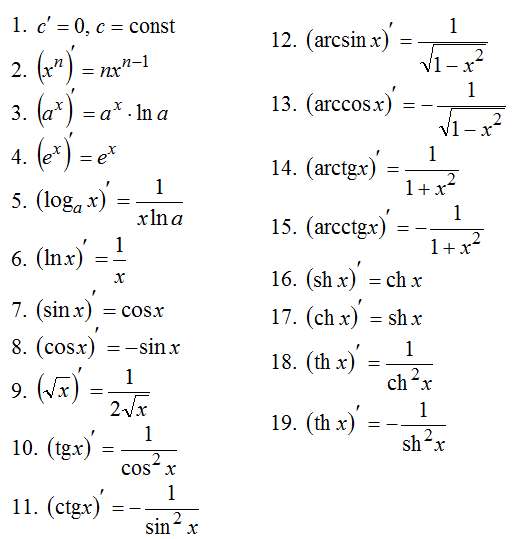
Производная сложной функции

Сложная функция это функция от функции. Следовательно, можно дать следующее определение сложной функции:

Определение: Функция вида y = f ( g (x) ) называется сложной функцией, составленной из функ­ций f u g, или суперпозицией функций f и g.

Пример: Функция у =ln(cos x) есть сложная функция, составленная из функций

у = lnuи u = cos x .

Поэтому сложную функцию часто пишут в виде

y = f(u), где u = g(x).

Внешняя функция Промежуточная функция

При этом аргумент х называют

---

независимой перемен­ной, а u - промежуточным аргументом.

Вернемся к примеру. Производную каждой из этих функций мы можем вычислить, используя таблицу производных.

Как же вычислить производную сложной функции?

Ответ на этот вопрос дает следующая теорема.

Теорема: Если функция u = g(x) дифференци­руема в некоторой точке х₀, а функция y=f(u) дифференцируема в точке u₀ = g(x₀), то сложная функция у=f(g(x)) дифференцируема в данной точке x₀.

При этом или ,

т.е. производная от у по переменной х равна производной от у по переменной и, умноженной на производную о т и по переменной х.

Правило:

1. 
   Чтобы найти производную сложной функции, надо ее правильно прочитать;
   
2. 
   Чтобы правильно прочитать функцию, надо определить в ней порядок действий;
   
3. 
   Функцию читаем в обратном порядку действий направлении;
   
4. 
   Производную находим по ходу чтения функции.
   

А теперь разберем это на примере:

Пример 1: Функция у =ln (cos x) получается последовательным выполнением двух операций: взятия косинуса угла х и нахождения от этого числа натурального логарифма:

.

Функция читается так: логарифмическая функция от тригонометрической функции.

Продифференцируем функцию: у = ln( cos x)=lnu, u=cosx.

.

На практике такое дифференцирование производится гораздо короче и проще, во всяком случае, без введения записи и.

Искусство дифференцирования сложной функции заключается в умении видеть в момент дифференцирования только одну функцию (именно - дифференцируемую в данный момент), не замечая пока другие, откладывая их видение до момента дифференцирования.

---

Будем использовать при дифференцировании дополненную таблицу производных.

.

Пример 2: Найти производную функции у = (x³ - 5х + 7)⁹.

Решение: Обозначив в «уме» u = х³ – 5x +7, получим у = u⁹. Найдем:

и

По формуле имеем

4. 
   Применение на практике полученных знаний.
   

Найти производные следующих функций.

1 2 3 4 5

6 7 8 9 10 +

11 12 13 14. ;

15.

---

.

При решении активизирую внимание класса путем рецензирования, исправления и дополнения ответов. Также даю возможность задавать вопросы преподавателю и отвечающим, что позволяет вовлекать большее число учеников в проверку знаний и способствует активному повторению материала.

5. 
   Контроль знаний.
   

1 вариант	2 вариант
1.	= ′
	2.
′	′
4 * ′	4* = ′
5* = ′	5* ′

---

6. Итоги урока.

Вопросы для самопроверки:

1) Верно ли, что:

а) если функции f(x) и g(x) дифференцируемы в точке , то в этой точке дифференцируема и функция ?

б) если функция f(x)=v(x)+u(x) дифференцируема в точке ,то функции u(x) и v(x) тоже дифференцируемы в этой точке.

2) Чему равна производная функции f(x) в точке , если, и функции u(x) и v(x) дифференцируемы в этой точке?

3) Чему равна производная функции f(x) в точке , если и функции u(x) и v(x) дифференцируемы в этой точке?

Отметить учащихся, активно работавших на уроке.

7. 
   Рефлексия. Домашнее задание.
   

Выучить п.___________решить №___________________

Урок по теме: « Уравнение касательной к кривой»

Цели:
• Отработать умения и навыки вычисления производной функции, нахождение производной функции в точке; вырабатывать у обучающихся умения и навыки в составлении уравнения касательной к графику функции  в точке;
• развивать внимание, зрительную память, логическое и образное мышление, познавательный интерес, активность учащихся на уроках;
• воспитывать аккуратность, прививать интерес к предмету, воспитывать познавательную активность, самостоятельность.

Ход урока.

1. 
   
   Тема сегодняшнего урока: «Уравнение касательной к графику функции». Откройте тетради, запишите число и тему урока.
   
   Пусть следующие слова станут девизом сегодняшнего урока.
   
   • 
     Плохих идей не бывает. Мыслите творчески. Рискуйте . Не критикуйте
     
   Орг. момент. Мотивация урока.
   

Чтобы настроиться на урок повторим ранее изученный материал.

2. 
   Актуализация опорных знаний. Проверка д/з.
   

На предыдущих уроках мы с вами находили производные различных функций. Какими формулами мы пользовались? (Формулами производной …)

Какие правила необходимо еще знать для нахождения производной функций? (Правила дифференцирования)
Сегодня мы применим наши знания и умения для того, чтобы больше узнать о производной и о других интересных фактах из истории математики.

Игра «Домино»
В комплекте «Домино» 20 карточек. Пары  перемешивают свои карточки, делят пополам  и начинают раскладывать домино с карточки. Если не все карточки разложены, значит, вы где - то допустили ошибку, и её нужно найти

---

Смотрите также файлы

• Целостность и безопасность государства.rtf

• Философия синергия вопросы от теста, для просмотра ответов, перейдите по ссылке ниже вопроса это специфическое средство отражения и выражения жизни в форме художественных образов,.docx

• Правила для младших школьников Безопасная дорога.pptx

• Формулировка.docx

• Реферат по теме принципы, свободы, мероприятия по защите от чс.docx