Файл: Урок алгебры в 11 классе по теме Предел функции в точке. Производная функции в точке. Геометрический и физический смысл производной..doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 25.10.2023
Просмотров: 111
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
В физике часто идёт речь о скорости v(t), т.е. скорости в определённый момент времени t, часто её называют мгновенной скоростью.
Можно рассуждать так: мгновенную скорость получим если Δt
Можно указать ещё много задач из физики, геометрии, для решения которых необходимо отыскать скорость изменения соответствующей функции.
Например, отыскание угловой скорости вращающегося тела, отыскание теплоёмкости тела при нагревании, линейный коэффициент расширения тел при нагревании, скорость химической реакции в данный момент времени и т.п.
Все эти задачи требуют для своего решения нахождения скорости изменения соответствующей функции.
Ввиду обилия задач, приводящих к вычислению скорости изменения функции или, иначе, к вычислению предела отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю, оказалось необходимым выделить такой предел для произвольной функции и изучить его основные свойства.
Этот предел называется производной функции.
II. Определение производной.
Определение: Производной функции y = f(x) в данной точке x0 называется предел отношения приращения функции в этой точке к приращению аргумента, при условии, что приращение аргумента стремится к нулю.
Обозначение производной:
Решение задач на закрепление понятия производной
Пример 1.
Найти производную функции y = C.
Решение: f(x) = C.
1.Возьмём два значения аргумента x и x + Δx.
2.
3.
4.
.
Значит,
Пример 2.
Найти производную функции y = x.
Решение: f(x) = x.
1.Возьмём два значения аргумента x и x + Δx.
2.
3.
4.
Значит,
Пример 3.
Найти производную функции y = x2.
Решение: f(x) = x2.
1.Возьмём два значения аргумента x и x + Δx.
2.
3.
4.
Значит,
Запишем найденные производные в таблицу и в дальнейшем будем ей пользоваться.
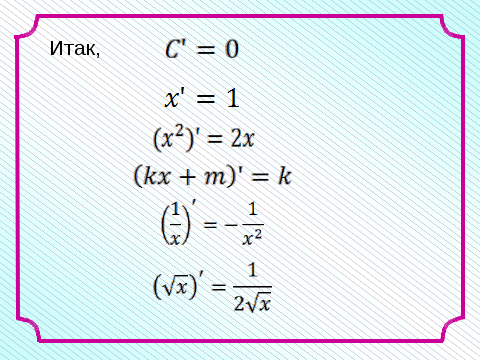
5. Самостоятельная работа
Вычислите: а)
б)
в)
г)
Решить № 539, 392, 406(а).
6. Домашнее задание.
Выучить п.9, 10, 14.
Решить № 393, 406(б), 540, 541.
7. Итог урока. Рефлексия.
Прием «Незаконченное предложение».
Ученикам предлагается высказать мнение по поводу урока.
Урок алгебры в 11 классе по теме «Правила дифференцирования и таблица производных.
Производная сложной функции»
Цель урока:
-
Формирование у учащихся представлений о правилах дифференцирования и таблице производных, изучить правило нахождения производной сложной функции; закрепить их при решении примеров;. -
Развитие внимания, памяти, логического мышления; -
Воспитание старательности, организованности.
Ход урока:
-
Организационный момент:
-
Взаимное приветствие, проверка рабочих мест, проверка отсутствующих. -
Создать благоприятный психологический настрой на работу.
Знания по данной теме будет нами использоваться на следующих уроках при исследовании функции для построения графика.
-
Актуализация опорных знаний. Проверка домашнего задания.
Что изучили на прошлом уроке и что было задано на дом? На прошлом уроке мы познакомились с понятием производной. Научились находить производную по её общему правилу (по определению) и обобщили эти знания, составив алгоритм нахождения производной по определению.
Самостоятельная работа по теме: «Пределы»
Вариант 1
-
Найти следующие пределы:
-
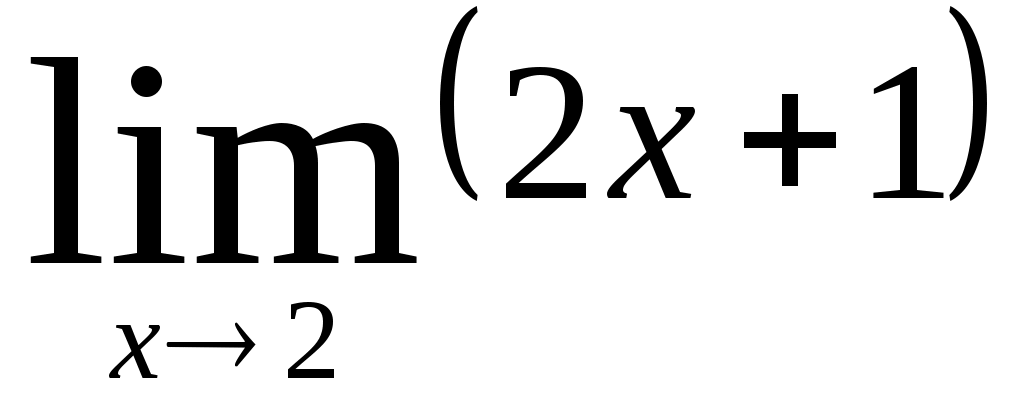 ; б)
; б) 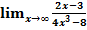 ; в)
; в) 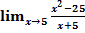 ; г)
; г) 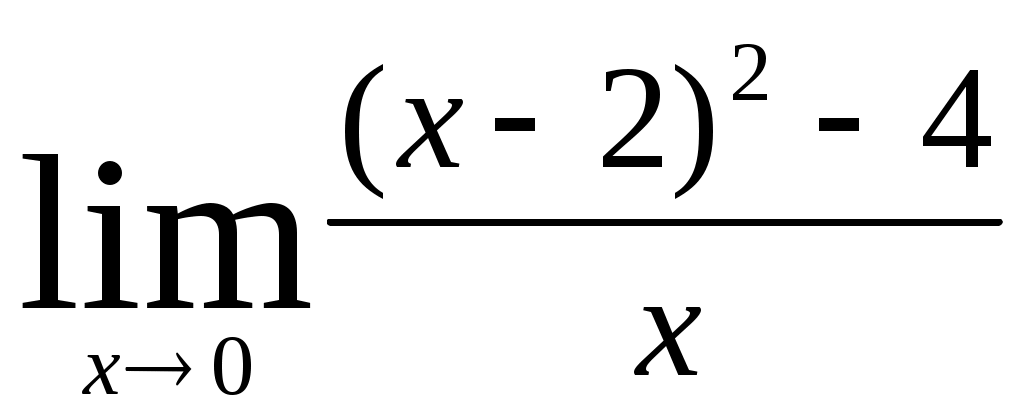 ;
;
д)
2. Дополнительное задание:
Вариант 2
-
Найти следующие пределы:
д)
-
Дополнительное задание:
Вопросы для повторения:
1) Что называется производной функции y = f(x) в точке x?
2) Как называется операция нахождение производной функции?
-
Изучение нового материала.
Историческая справка о дифференциальном исчислении
Дифференциальное исчисление – это раздел математики, в котором изучаются производные и их применение к исследованию функций. Приращения вида
Термин «производная» является буквальным переводом на русский язык французского слова derivee, которое ввел в 1797 году Ж. Лагранж. Он же ввел современные обозначения f′ и y′. Г. Лейбниц говорил о дифференциальном отношении и обозначал производную как df/dx. Это обозначение встречается и в современной литературе.
Производная – одно из фундаментальных понятий математики. Оно возникло в XVII в. в связи с необходимостью решения ряда задач из физики, механики и математики, но в первую очередь для определения скорости прямолинейного движения и построения касательной к кривой.
Независимо друг от друга И. Ньютон и Г. Лейбниц разработали аппарат исчисления, которым мы пользуемся в настоящее время. Ньютон исходил в основном из задач механики (опирался на физическое представление о мгновенной скорости движения, считая его очевидным и, сводя к нему другие случаи производной), а Лейбниц по преимуществу исходил из геометрических задач (использовал понятие бесконечно малой).Исчисление, созданное Ньютоном и Лейбницем, получило название дифференциального исчисления. Но задолго до этого многие ученые решали задачи, связанные с производной.
Учёные, которые внесли свой вклад в развитие дифференциального исчисления.
Теорема 1. Производная суммы двух дифференцируемых функций равна сумме производных этих функций.
Доказательство (доказательство проводит учитель):
Есть функции u(x) и v(x); и .
Нужно доказать, что (u(x)+v(x))' = u'(x)+v'(x).
Пусть u(x) + v(x) = f(x).
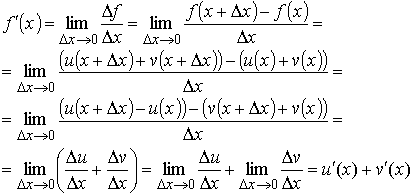
Значит, (u(x)+v(x))' = u'(x)+v'(x). ЧТД
Замечание 1: Аналогично можно доказать, что (u(x)-v(x))'=u'(x)-v'(x).
Замечание 2: Можно доказать справедливость теоремы 1 для суммы любого конечного числа дифференцируемых функций, т.е.
Задача 1: Найти производную функции f(x)=x2+x – 7. Вычислить f (-1), f (0), f (3)
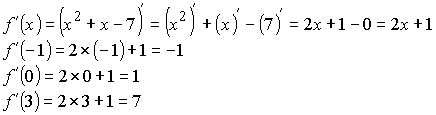
Теорема 2. Производная произведения двух дифференцируемых функций равна сумме произведений каждой функции на производную другой.
Доказательство (доказательство проводит учитель):
Есть функции u(x) и v(x); и .
Нужно доказать, что .
Пусть
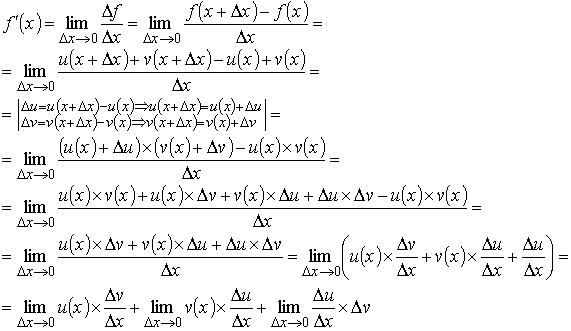
Множители и не зависят от . Функция v(x) имеет производную, поэтому она непрерывна и .
Имеем:
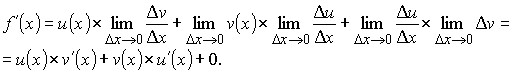
Мы доказали, что .
Эта формула называется формулой Лейбница.
Замечание: Можно доказать, что производная произведения любого конечного числа множителей равна сумме произведений производной каждого из них на все остальные.
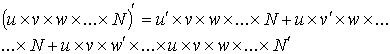
Следствие 1. (доказательство проводят ученики самостоятельно)
Постоянный множитель можно выносить за знак производной. .
Доказательство:
По теореме 2 имеем:
Но , поэтому
Следствие 2. Производная функции f(x)=xn, где равна произведению показателя n на степень .
Доказательство (доказательство проводят ученики самостоятельно):
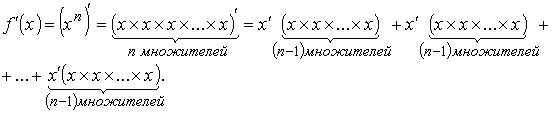
Но , ,а число слагаемых равно числу множителей n, поэтому имеем .
Эта формула верна любого n.
Таким образом, производная степной функции:
Задача 2. Найти производную функции f(x)=x3(x-1)
Решение:
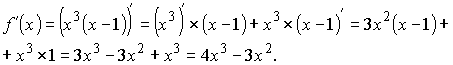
Учитель обращает внимание на то, что ранее мы искали производную, используя только определение, теперь же, зная правила дифференцирования, процесс отыскания производной стал гораздо проще.