Файл: Урок алгебры в 11 классе по теме Предел функции в точке. Производная функции в точке. Геометрический и физический смысл производной..doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 25.10.2023
Просмотров: 113
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
- 12 y' =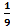 Р
Р
y' = 1 Т
y' = -12 Г
5) y=x4 y' =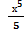 П
П
y' = 4x3 А
y' = x3 С
6) y=-5x3 y' = -15x2 Н
y' = -5x2 О
y' = 5x2 Р
7) y=x-x3y' = 1-x2 Д
y' = 1-3x2 Ж
y' = x-3x2 А
Итак, получили фамилию ученого Лагранж.
«Заметки из прошлого» Жозеф Луи Лагранж. Уже в 1755 году внес огромный вклад в разные области математики и в том числе на нахождение максимумов и минимумов функции.
Фронтальная работа
А теперь дадим некоторые определения свойствам функции “Мозговой штурм”
Интервалы возрастания и убывания функции называются интервалами монотонности функции.
ТЕОРЕМА 1 (необходимое и достаточное условия возрастания (убывания) функции). Пусть функция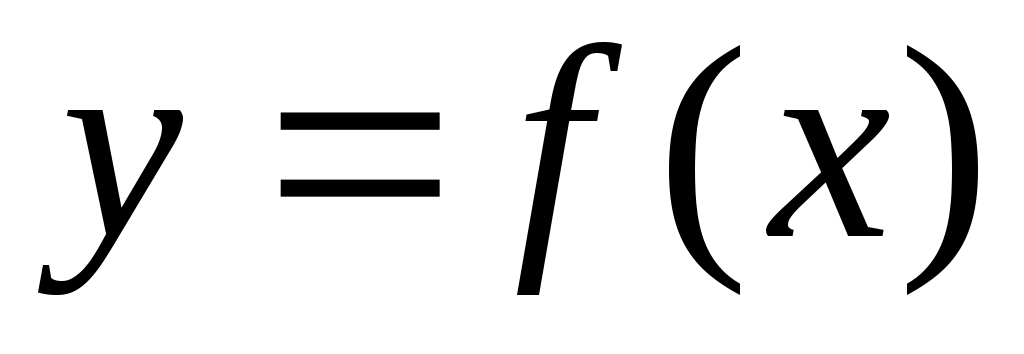 дифференцируема на интервале
дифференцируема на интервале  . Тогда
. Тогда
1) если функция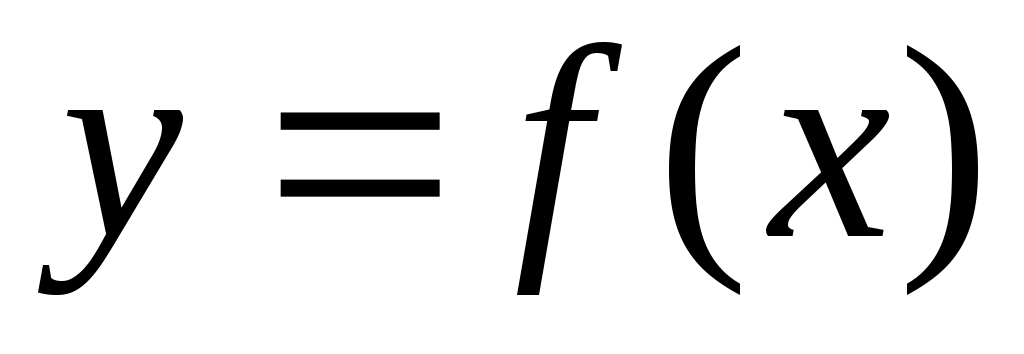 возрастает (убывает) на
возрастает (убывает) на 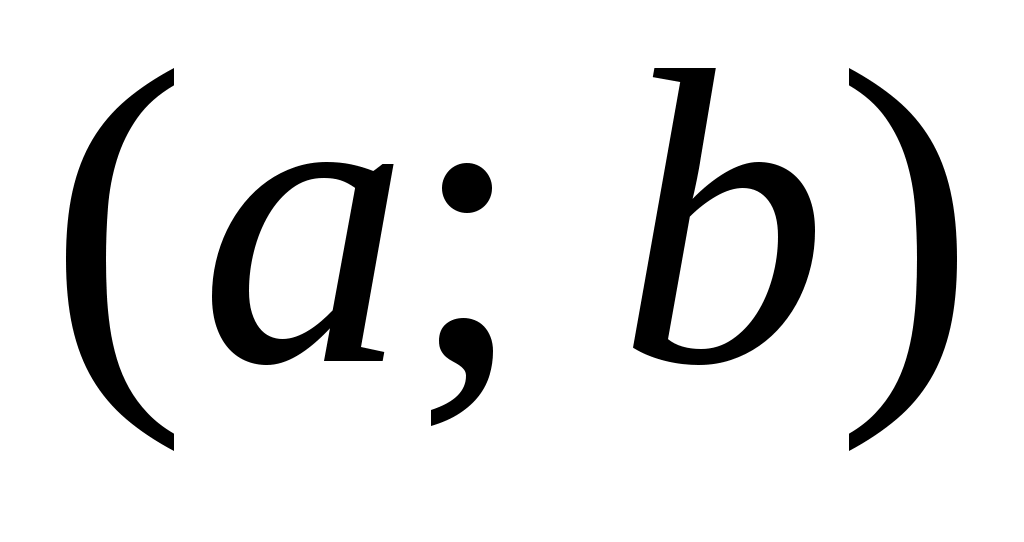 , то на этом интервале ее производная неотрицательна (неположительна),
, то на этом интервале ее производная неотрицательна (неположительна),
т.е.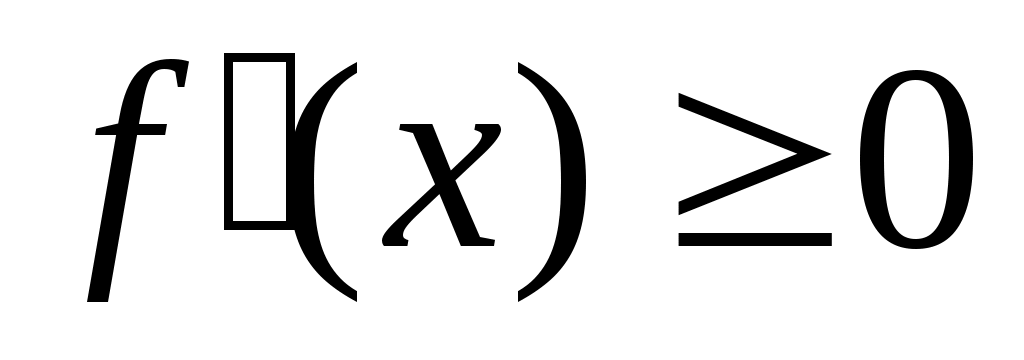 ,
, 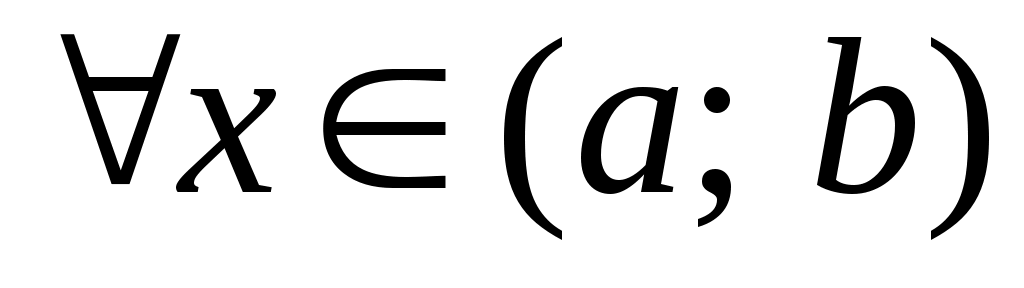 (
(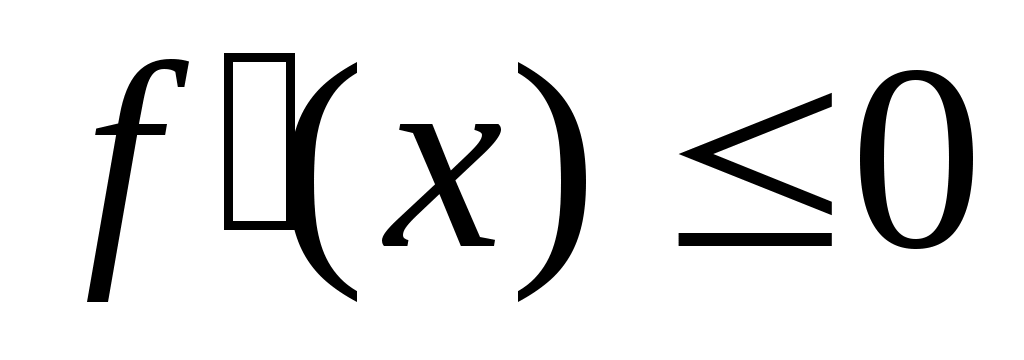 ,
, 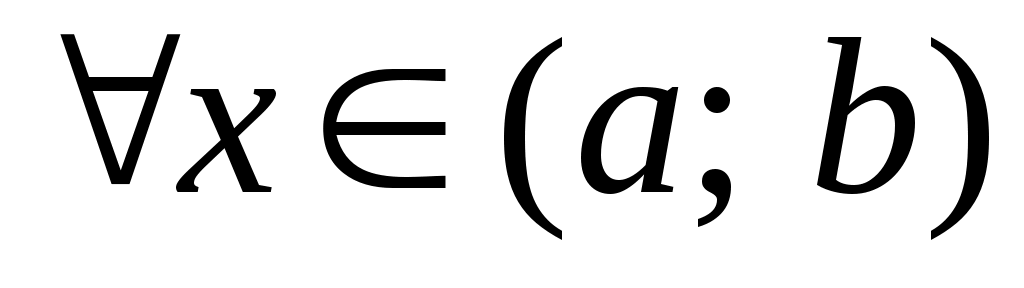 );
);
2) если производная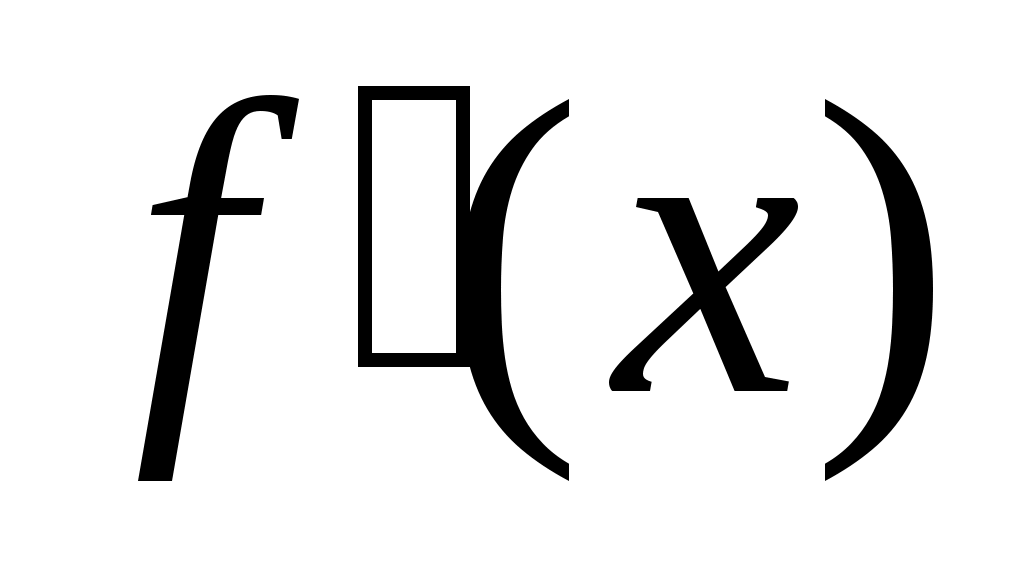 на интервале
на интервале 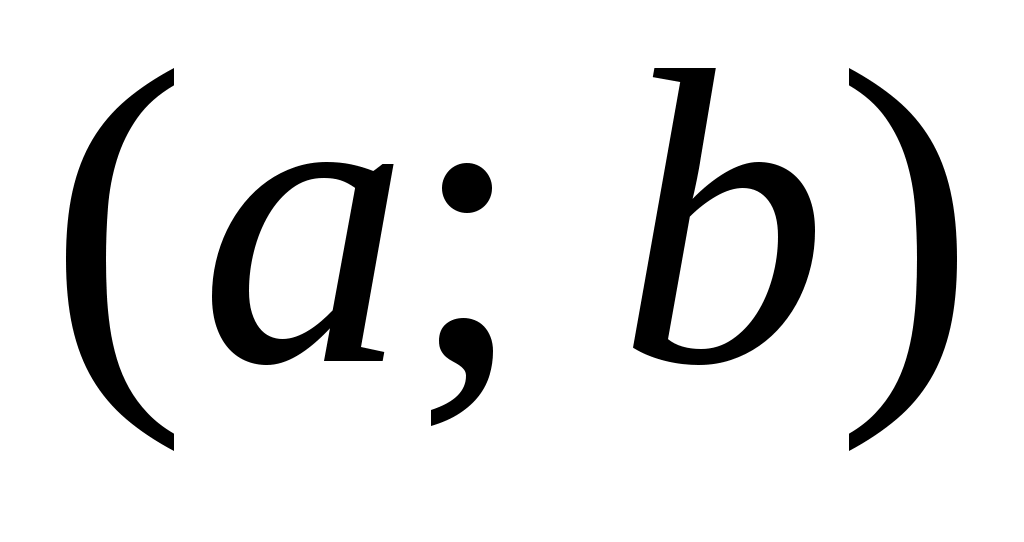 положительна (отрицательна), т.е.
положительна (отрицательна), т.е. 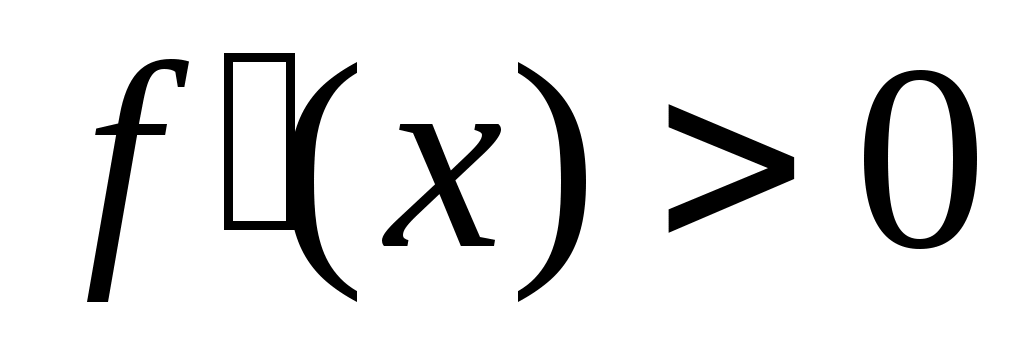 ,
, 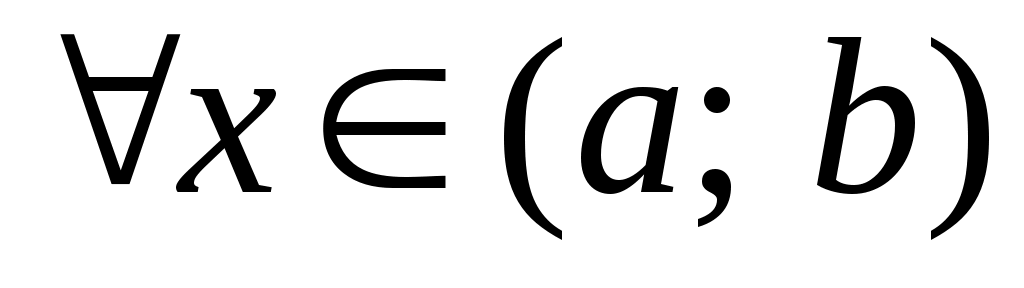 (
(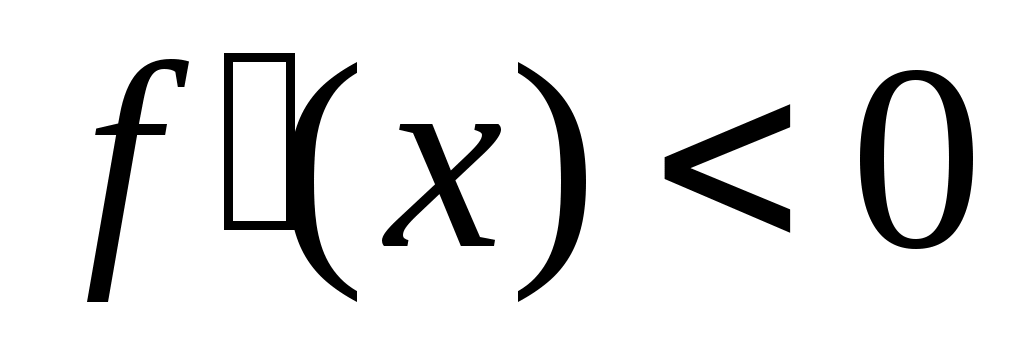 ,
, 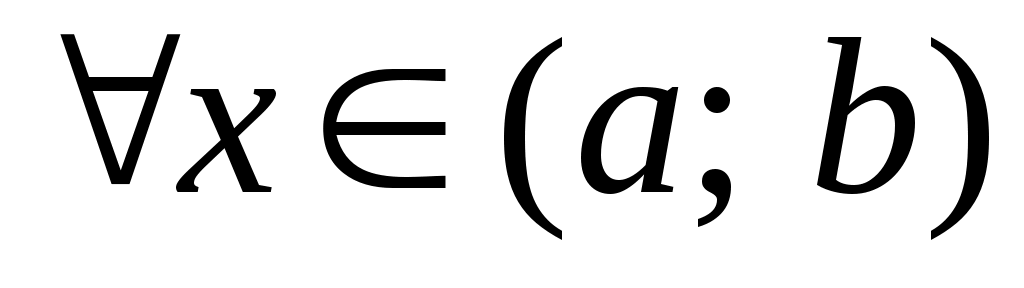 ),
),
т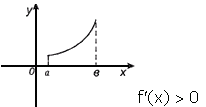
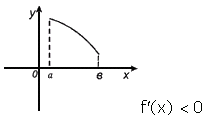
о функция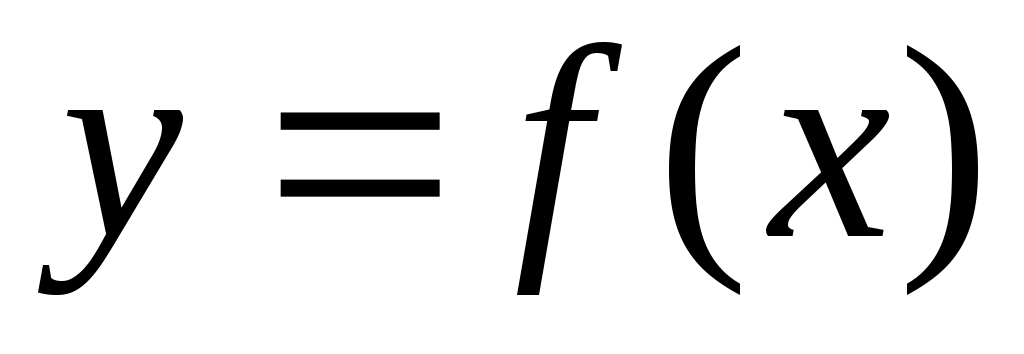 на
на 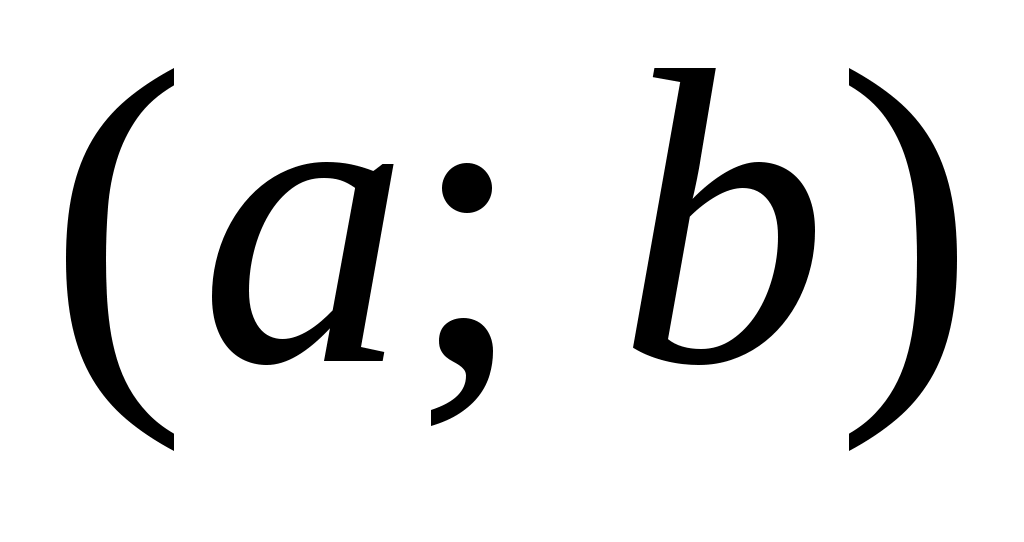 возрастает (убывает).
возрастает (убывает).
Решение. Найдем производную функции y = 4x3 – 5x2 + 2: y’ = 12x2 -10x. Решая неравенство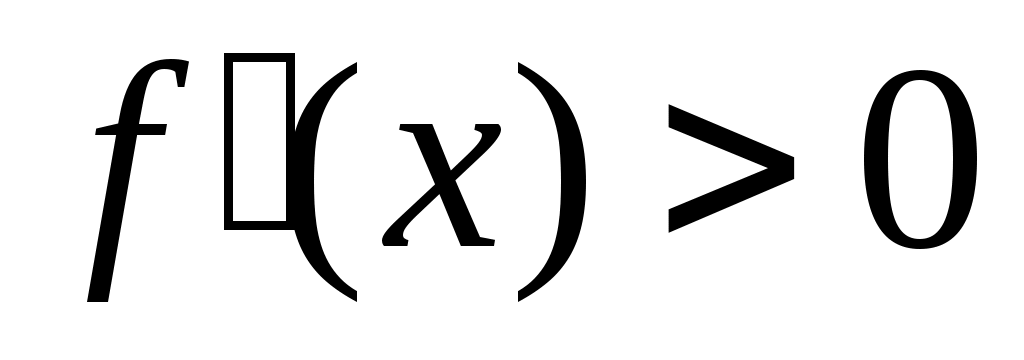
, получим x(12x – 10) > 0, отсюда x > 5/6, x < 0 - промежутки возрастания. Решая неравенство , получим x(12x – 10) < 0, отсюда 0 < x < 5/6 - промежуток убывания.
, получим x(12x – 10) < 0, отсюда 0 < x < 5/6 - промежуток убывания.
Экстремумы функции
Пусть функция определена на множестве
определена на множестве 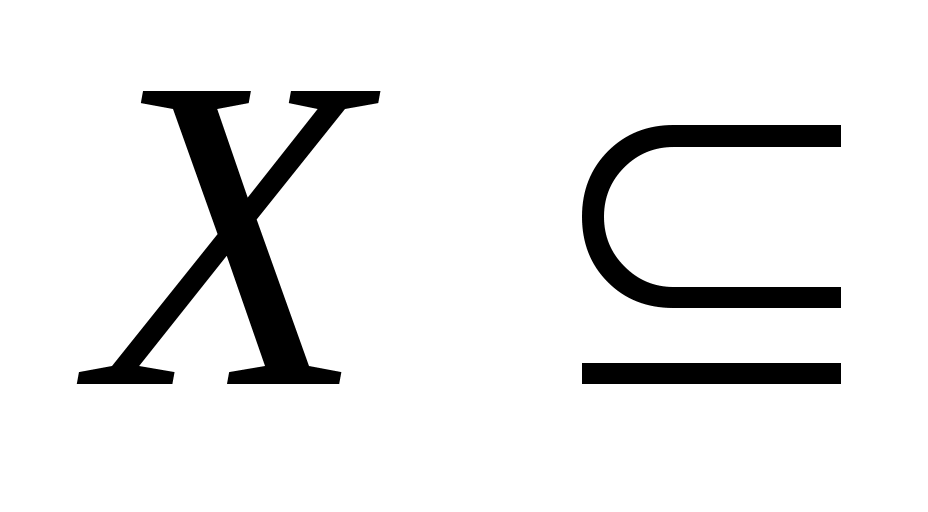 ℝ,
ℝ,  ,
, 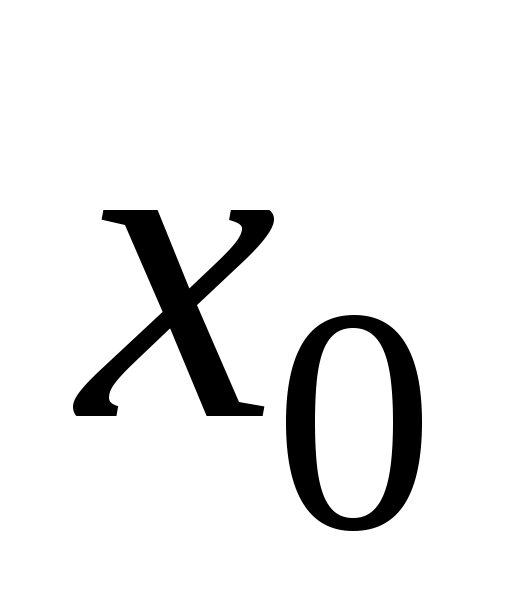 – внутренняя точка
– внутренняя точка 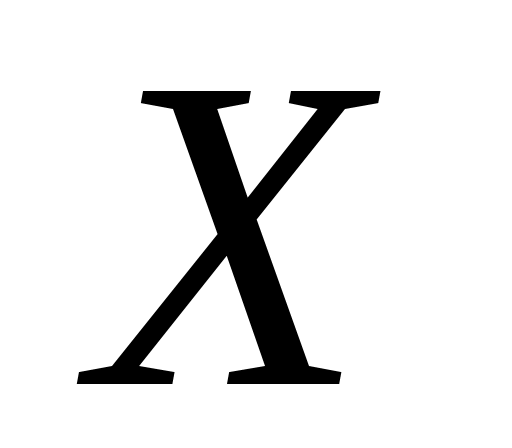 (т.е. существует некоторая окрестность точки
(т.е. существует некоторая окрестность точки 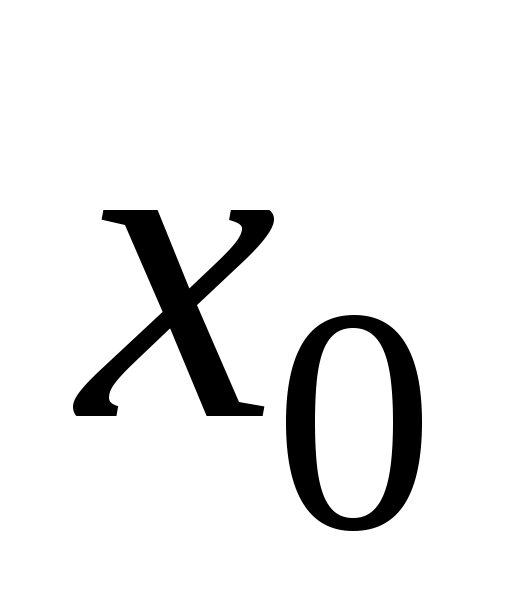 , целиком лежащая во множестве
, целиком лежащая во множестве 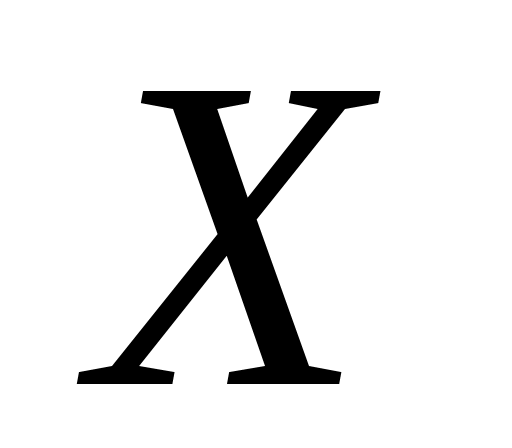 ).
).
ОПРЕДЕЛЕНИЕ. Точка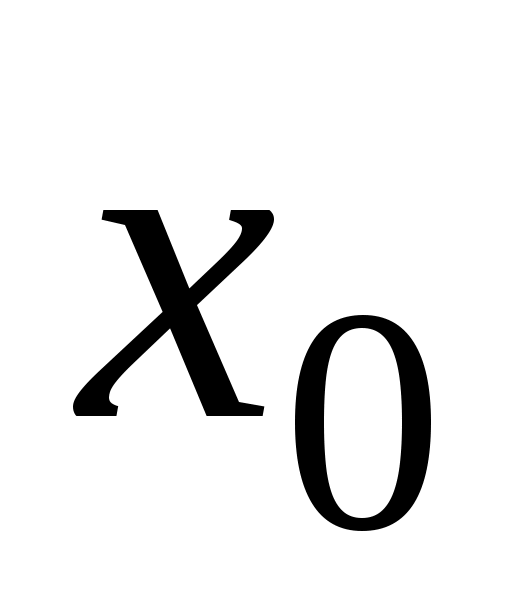 называется точкоймаксимумафункции
называется точкоймаксимумафункции 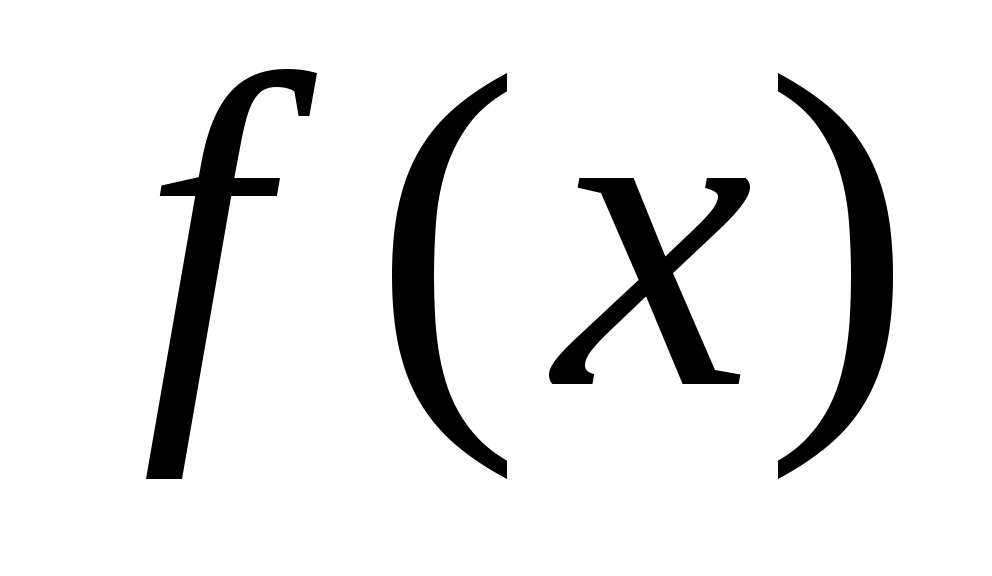 если существует такая
если существует такая 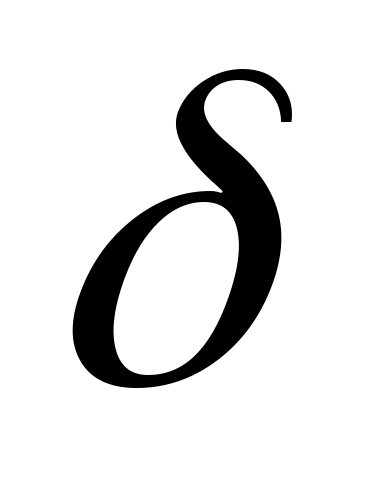 -окрестность
-окрестность 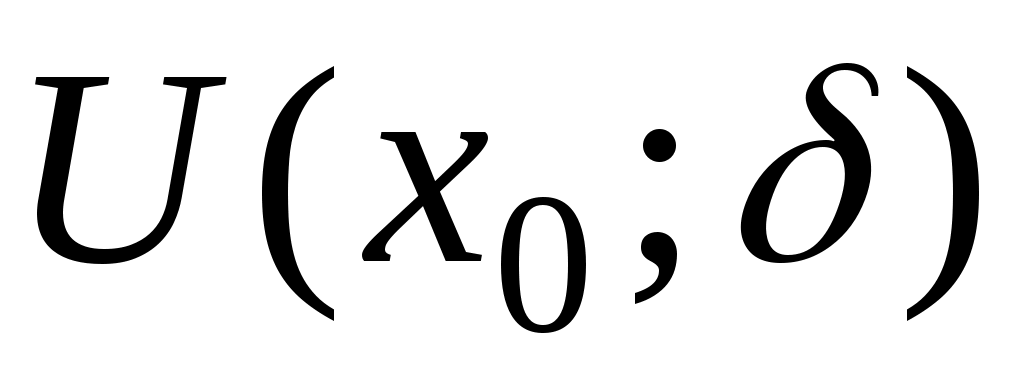 точки
точки 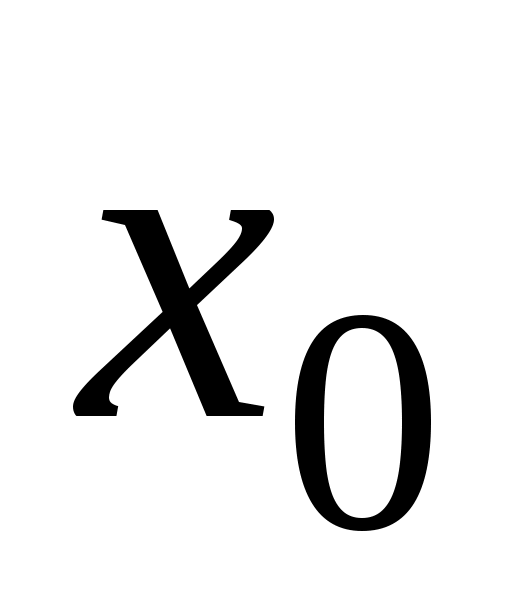 , что
, что 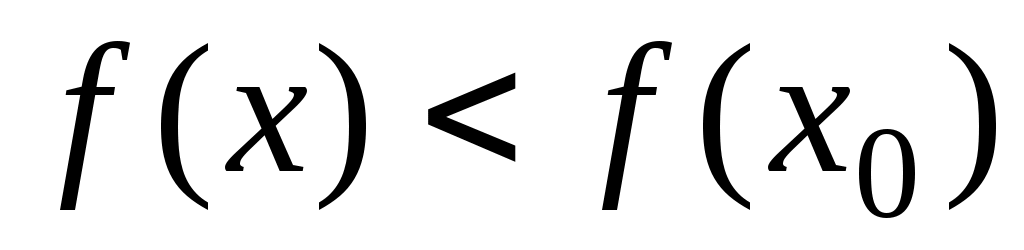 ,
, 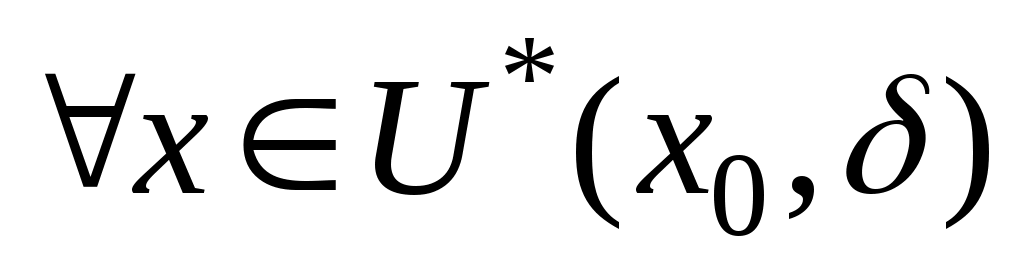 . Значение функции в точке максимума называется максимумом функции.
. Значение функции в точке максимума называется максимумом функции.
Точка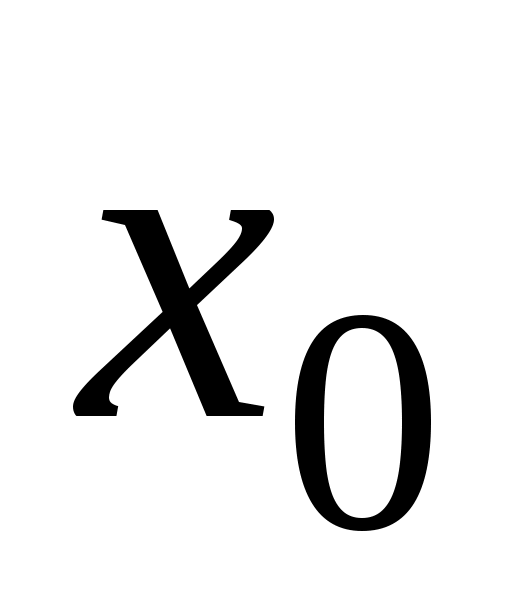 называется точкойминимума функции
называется точкойминимума функции 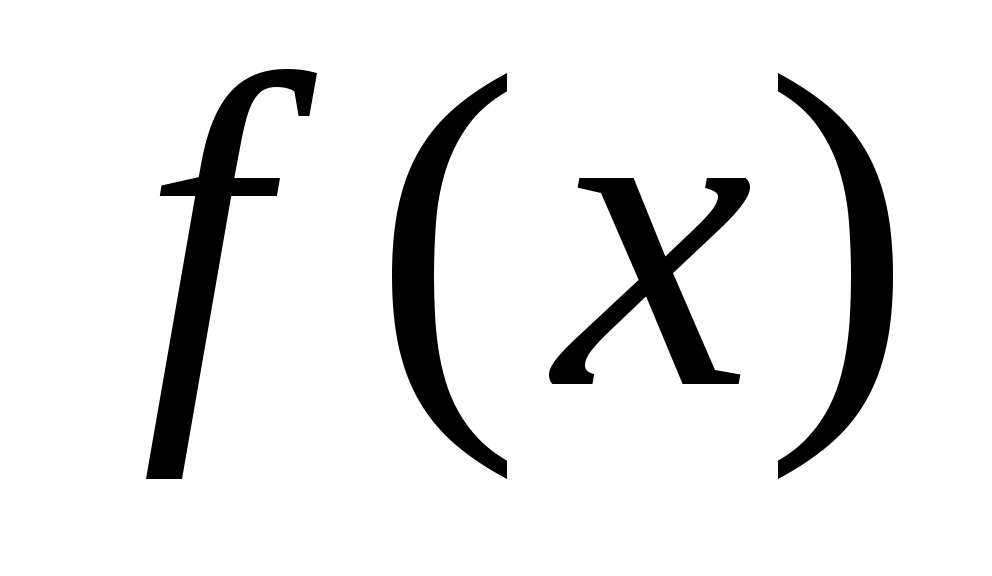 если существует такая
если существует такая 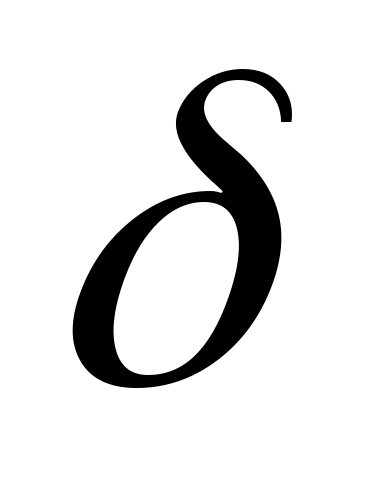 -окрестность
-окрестность 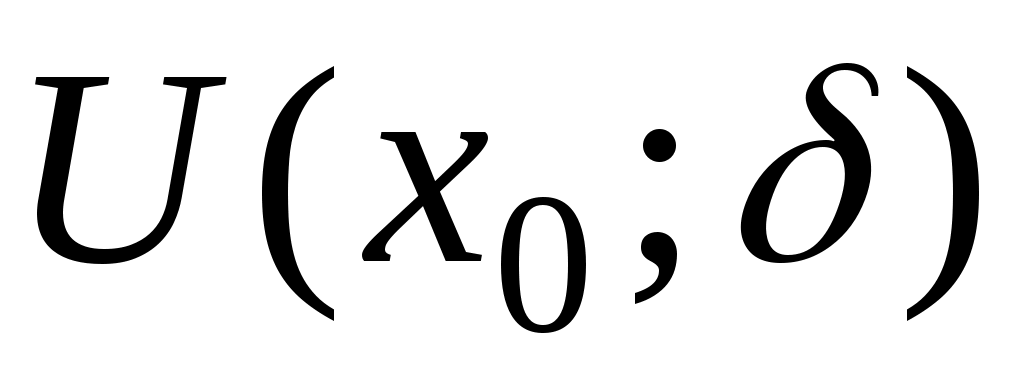 точки
точки 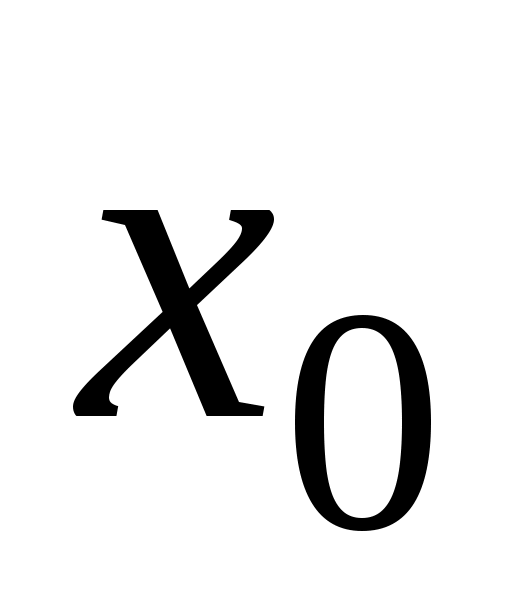 , что
, что 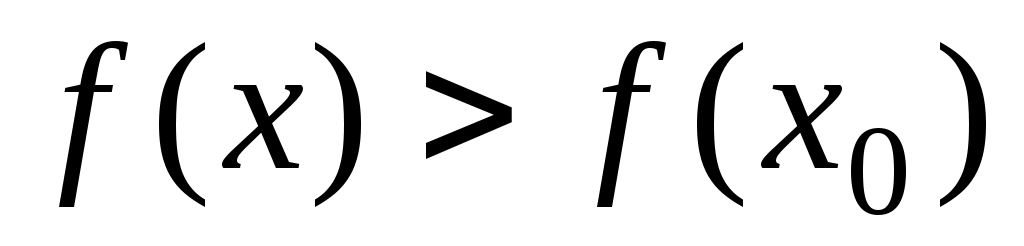 ,
, 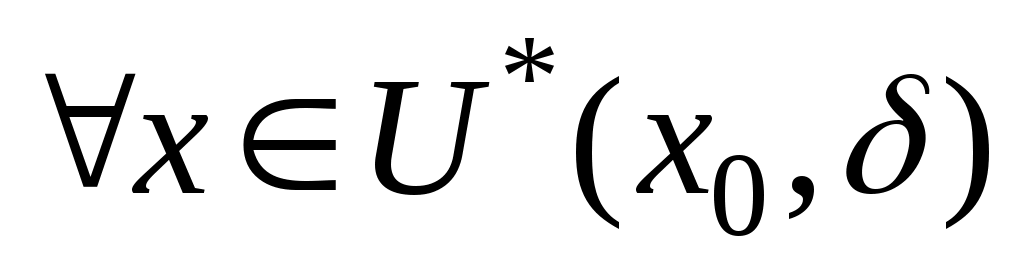 . Значение функции в точке минимума называется
. Значение функции в точке минимума называется
минимумомфункции.
Т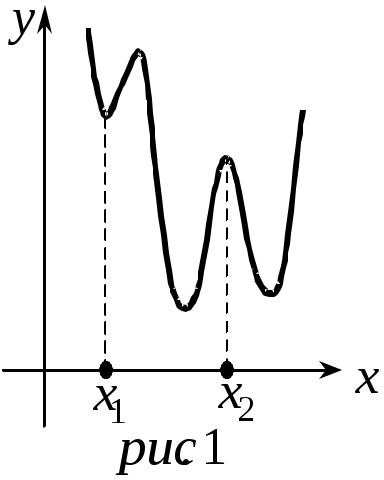 очки минимума и максимума функции называются ее точкамиэкстремума.
очки минимума и максимума функции называются ее точкамиэкстремума.
Замечания:
1) Понятия минимум и максимум функции близки к понятиям наименьшее и наибольшее значения функции. По сути, они отражают одно свойство функции: они показывают, в каком отношении находятся значение функции в данной точке и значения функции в других точках. Различие в области действия этих понятий. Наибольшее и наименьшее значения – понятия глобального характера (« »), максимум и минимум – понятия локального характера («
»), максимум и минимум – понятия локального характера (« »). Чтобы подчеркнуть эту взаимосвязь понятий, в некоторой литературе употребляют термины «глобальный максимум (минимум)» вместо наибольшего (наименьшего) значения функции и «локальный максимум (минимум)» – вместо максимум (минимум) функции.
»). Чтобы подчеркнуть эту взаимосвязь понятий, в некоторой литературе употребляют термины «глобальный максимум (минимум)» вместо наибольшего (наименьшего) значения функции и «локальный максимум (минимум)» – вместо максимум (минимум) функции.
2) В силу локального характера понятий максимума и минимума, функция может иметь в своей области определения несколько точек максимума и минимума. Причем, некоторые минимумы функции могут быть больше ее максимумов (см. рис. 1).
Для функции, дифференцируемой в точке , справедлива следующая теорема.
, справедлива следующая теорема.
ТЕОРЕМА 2 (необходимое условие экстремума, теорема Ферма). Если – точка экстремума функции
– точка экстремума функции  и
и  – дифференцируема в точке
– дифференцируема в точке  , то ее производная в этой точке равна нулю.
, то ее производная в этой точке равна нулю.
Алгоритм исследования непрерывной функции у=f(х) на монотонность и экстремумы:
Пример: Найдите точки экстремума функции: у=3х4
-16х3+24х2-14.
Решение: 1. f '(х) = 12х3-48х2+48х;
2. f '(х) = 0, 12х3-48х2+48х = 0;
12х(х2-4х+4)=0;
12х=0 или х2-4х+4=0;
х1=0, х2=2.
3. f (-1) = 3·(-1)4-16·(-1)3+24·(-1)2-11=3+16+24-14= + 29,
f (1) = 3·14-16·13+24·12-14=3-16+24-14=-3,
f (3) = 3·34-16·33+24·32-14= 243-384+216-14= + 51,
Исследование функции с помощью производной.
Схема исследования функции.
П РИМЕР. Построить график функции y = 1 + 2x2 – x4.
РИМЕР. Построить график функции y = 1 + 2x2 – x4.
Возрастает при y’ > 0, т.е. x < -1, 0 < x < 1
Убывает при y’ < 0, т.е. – 1 < x < 0, x > 1
y' = 1 Т
y' = -12 Г
5) y=x4 y' =
y' = 4x3 А
y' = x3 С
6) y=-5x3 y' = -15x2 Н
y' = -5x2 О
y' = 5x2 Р
7) y=x-x3y' = 1-x2 Д
y' = 1-3x2 Ж
y' = x-3x2 А
Итак, получили фамилию ученого Лагранж.
«Заметки из прошлого» Жозеф Луи Лагранж. Уже в 1755 году внес огромный вклад в разные области математики и в том числе на нахождение максимумов и минимумов функции.
Фронтальная работа
А теперь дадим некоторые определения свойствам функции “Мозговой штурм”
-
Что называют функцией? -
Как называется переменная Х? -
Как называется переменная Y? -
Что называется областью определения функции? -
Что называется множеством значения функции? -
Какая функция называется чётной? -
Какая функция называется нечётной? -
Что можно сказать о графике чётной функции? -
Что можно сказать о графике нечётной функции? -
Какая функция называется возрастающей? -
Какая функция называется убывающей? -
Какая функция называется периодической?
-
Изучение нового материала
Возрастание и убывание функции
Интервалы возрастания и убывания функции называются интервалами монотонности функции.
ТЕОРЕМА 1 (необходимое и достаточное условия возрастания (убывания) функции). Пусть функция
1) если функция
т.е.
2) если производная
т
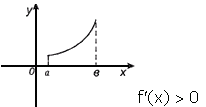
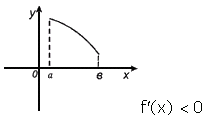
о функция
ПРИМЕР: Найти промежутки возрастания и убывания функции y = 4x3 – 5x2 + 2.
Решение. Найдем производную функции y = 4x3 – 5x2 + 2: y’ = 12x2 -10x. Решая неравенство
, получим x(12x – 10) > 0, отсюда x > 5/6, x < 0 - промежутки возрастания. Решая неравенство
Экстремумы функции
Пусть функция
ОПРЕДЕЛЕНИЕ. Точка
Точка
минимумомфункции.
Т
 очки минимума и максимума функции называются ее точкамиэкстремума.
очки минимума и максимума функции называются ее точкамиэкстремума. Замечания:
1) Понятия минимум и максимум функции близки к понятиям наименьшее и наибольшее значения функции. По сути, они отражают одно свойство функции: они показывают, в каком отношении находятся значение функции в данной точке и значения функции в других точках. Различие в области действия этих понятий. Наибольшее и наименьшее значения – понятия глобального характера («
2) В силу локального характера понятий максимума и минимума, функция может иметь в своей области определения несколько точек максимума и минимума. Причем, некоторые минимумы функции могут быть больше ее максимумов (см. рис. 1).
Для функции, дифференцируемой в точке
ТЕОРЕМА 2 (необходимое условие экстремума, теорема Ферма). Если
Алгоритм исследования непрерывной функции у=f(х) на монотонность и экстремумы:
-
Найти производную функции; -
Найти стационарные и критические точки: f´(х)=0 -
Отметить стационарные точки на числовой прямой и определить знаки производной на получившихся промежутках. Сделать вывод о монотонности функции и точках экстремума.
Пример: Найдите точки экстремума функции: у=3х4
-16х3+24х2-14.
Решение: 1. f '(х) = 12х3-48х2+48х;
2. f '(х) = 0, 12х3-48х2+48х = 0;
12х(х2-4х+4)=0;
12х=0 или х2-4х+4=0;
х1=0, х2=2.
3. f (-1) = 3·(-1)4-16·(-1)3+24·(-1)2-11=3+16+24-14= + 29,
f (1) = 3·14-16·13+24·12-14=3-16+24-14=-3,
f (3) = 3·34-16·33+24·32-14= 243-384+216-14= + 51,
Исследование функции с помощью производной.
Схема исследования функции.
-
Найти область определения функции. -
Точки пересечения с осями координат. -
Проверить на четность (нечетность). Четная функция симметрична относительно оси ординат, нечетная – относительно начала координат. -
Производную. -
Стационарные точки. -
Промежутки возрастания и убывания. -
Точки экстремума и значения функции в этих точках. -
Результаты исследования занести в таблицу.
П
 РИМЕР. Построить график функции y = 1 + 2x2 – x4.
РИМЕР. Построить график функции y = 1 + 2x2 – x4.-
Область определения:
-
x = 0, y = 1: A( 0, 1); -
y(-x) = 1 + 2(-x)2 – (-x)4 = 1 + 2x2 – x4 – функция четная. -
y’ = 4x – 4x3 = 4x(1 – x2) = 4x(1 – x)(1 + x) -
y’ = 4x(1 – x2) = 0; x1 = 0, y1 = 1; x2 = 1, y2 = 2; x3 = - 1, y3 = 2 -
4
x(1 – x)(1 + x) = 0
Возрастает при y’ > 0, т.е. x < -1, 0 < x < 1
Убывает при y’ < 0, т.е. – 1 < x < 0, x > 1
-
Точки ( -1, 2) и (1, 2) точки max; (0, 1) – min. -
Заполняем таблицу:
| x | x < -1 | - 1 | – 1 < x < 0 | 0 | 0 < x < 1 | 1 | x > 1 | 2 |
| f ‘(x) | + | 0 | - | 0 | + | 0 | - | |
| f(x) |  | 2 |  | 1 |  | 2 |  | - 7 |