Файл: Курсовая работа по дисциплине Теория электрической связи (наименование учебной дисциплины согласно учебному плану).docx
Добавлен: 25.10.2023
Просмотров: 146
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
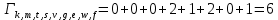
Метрика путей из k в z:
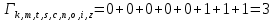
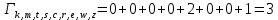
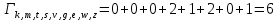


Рисунок 37 — Решетчатые диаграммы декодера между моментами
 и
и 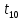 : а) с возможными путями, б) только с выжившими
: а) с возможными путями, б) только с выжившимиМетрика путей из k в g:
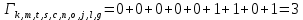
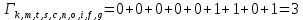
Метрика путей из k в e:
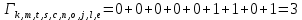
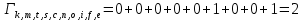
Метрика путей из k в r:
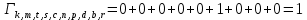
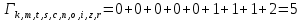
Метрика путей из k в w:
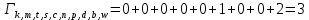
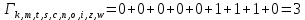
Выживший путь из оставшихся:
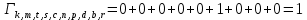

Рисунок 38 — Решетчатая диаграммы декодера между моментами
 и
и 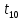 с единственным выжившим путём
с единственным выжившим путёмНайденный путь (рис. 38) полностью совпадает с путём на диаграмме свёрточного кодера. Следовательно, ошибка на выходе демодулятора была исправлена.
| Информационные символы (ИС)  | 1 | 1 | 1 | 0 | 0 | 1 | 0 | 1 | 0 |
| Кодовые символы (КС)  на выходе кодера на выходе кодера | 11 | 01 | 10 | 01 | 11 | 11 | 10 | 00 | 10 |
| Последовательность на входе декодера  | 11 | 01 | 10 | 01 | 11 | 01 | 10 | 00 | 10 |
| Последовательность на выходе декодера  | 11 | 01 | 10 | 01 | 11 | 11 | 10 | 00 | 10 |
Таблица 4 — Последовательности символов на разных этапах кодирования и декодирования
ЗАКЛЮЧЕНИЕ
Курсовая работа выполнена в полном объёме, все задачи решены верно.
В ходе выполнения курсовой работы были изучены принципы работы современных цифровых систем связи с использованием квадратурных видов модуляции, которые оптимальны в отношении флуктуационной помехи (типа белого шума).
Рассчитаны основные характеристики случайных сигналов на выходе источника сообщений, на выходе АЦП.
В качестве алгоритма кодирования был применен алгоритм свёрточного кодирования Витерби.
Для модулятора выбрана КФМ – 4 с использованием соответстующего сигнального созвездия.
Рассмотрены определения вероятностных характеристик случайных процессов на выходах соответствующих функциональных узлов (корреляционные функции и спектральные плотности мощности).
Приведён подробный вывод корреляционной функции для случайного синхронного телеграфного сигнала в разд. 1.4.
Построен график корреляционной функции на выходах СФФ, перемножителей в составе модулятора.
Построены графики сигналов на выходе квадраттурных модуляторов; на входе блока ФМС.
Приведена структурная схема квадратурного демодулятора с обоснованием алгоритма работы решающих устройств (РУ). Определены вероятности ошибок на выходах РУ с последующим перерасчетом вероятности ошибок на выходе преобразователя параллельного кода в последовательный код.
Исправлены ошибки на выходе демодулятора с использованием декодирования на основе алгоритма Витерби.
Из всего вышесказанного следует, что цель работы достигнута.
СПИСОК ЛИТЕРАТУРЫ
1. Зюко, А. Г. Теория передачи сигналов / А. Г. Зюко, Д. Д. Кловский, М. В. Назаров,
Л. М. Финк. – Изд. 2-е, перераб. и доп. – М. : Радио и связь, 1986. – 304 с.
2. Зюко, А. Г. Теория электрической связи : учебник для вузов / А. Г. Зюко,
Д. Д. Кловский, В. И. Коржик, М. В. Назаров. – М. : Радио и связь, 1998.
3. Прокис, Дж. Цифровая связь : пер. с англ. / Дж. Прокис ; под ред. Д. Д. Кловского. – М. : Радио и связь, 2000. – 800 с.
4. Галкин, В. А. Цифровая мобильная радиосвязь : учеб. пособие для вузов /
В. А. Галкин. – М. : Горячая линия – Телеком, 2007 – 432 с.
5. Гоноровский, И. С. Радиотехнические цепи и сигналы : учеб. для вузов / И. С. Гоноровский. – Изд. Радио и связь, 1977.
6. Куликов, Л. Н. Теория электрической связи. Основы сверточного кодирования :
учеб. пособие / Л. Н. Куликов, М. Н. Москалец. – СПб., 2006.
7. Куликов, Л. Н. Общая теория связи : методические указания к выполнению
курсовой работы / Л. Н. Куликов, М. Н. Москалец, М. Н. Чесноков. – СПб., 2012.
8. Григоровский, Л. Ф. Теория электрической связи. Модели сигналов и методы их преобразования в системах связи : учеб. пособие / Л. Ф. Григоровский,
В. И. Коржик, В. Г. Красов, В. Ф. Кушнир. – Л. : ЛЭИС. – 1990.
9. Тихонов, В. И. Статистическая радиотехника / В. И. Тихонов. – Изд. 2-е, перераб. и доп. – М. : Радио и связь, 1982. – 624 с.
10. Сальников, А. П. Теория электрической связи : конспект лекций / А. П. Сальников. – СПб. : Линк, 2007.
11. Скляр, Бернард. Цифровая связь. Теоретические основы и практическое применение : пер. с англ. / Бернард Скляр. – Изд. 2-е, испр. – М. : Издательский дом
«Вильямс», 2003. – 1104 с.
12. Биккенин, Р. Р. Теория электрической связи : учеб. пособие / Р. Р. Биккенин,
М. Н. Чесноков. – Л. : ЛЭИС. – 2010.
13. Кларк, Дж. Кодирование с исправлением ошибок в системах цифровой связи /
Дж. Кларк, мл. Дж. Кейн ; пер. с англ. С. И. Гельфонда ; под ред. Б. С. Цыбакова. – М. :
Радио и связь, 1987. – Вып. 28. – 392 с.
14. Атабеков, Г. И. Основы теории цепей : учебник для вузов / Г. И. Атабеков. –
М. : Энергия, 1969. – 424 с.
15. Френкс, Л. Теория сигналов : пер. с англ. / Л. Френкс ; под ред. Д. Е. Вакмана. –
М. : Советское радио, 1974. – 344 с.
16. Бронштейн, И. Н. Справочник по математике для инженеров и учащихся втузов / И. Н. Бронштейн, К. А. Семендяев. – М. : Наука, 1964.
Приложение А
Приведён код из программы MATLAB
% плотность вероятности----------------------------------------------------
syms x
y = piecewise( x < 0, 0, 0 < x < 5 , 0.2, x > 5, 0);
fplot(y)
xlim([ -1 6 ])
ylim([ 0 0.21 ])
grid
xlabel( 'a' )
ylabel( 'w(a)' )
% ф-ия распределения-------------------------------------------------------
syms a
f = piecewise( a < 0, 0, 0 < a < 5 , 0.2*a , a > 5, 1);
fplot( f )
xlim([ -1 6 ])
ylim([ 0 1 ])
grid
xlabel( 'a' )
ylabel( 'F(a)' )
% спектральная плотность мощности------------------------------------------
syms g
f = piecewise( g < -4100, 0, -4100 < g < 4100 , 0.000254065, g > 4100, 0);
hold on
fplot( f )
xlim([ -5000 5000 ])
ylim([ 0 0.00027 ])
grid
xlabel( 'f' )
ylabel( 'G(f)' )
% корреляционная ф-ия------------------------------------------------------
syms t
B = 2.54065*10^( -4 )*sin( 8200*pi*t )/( pi*t );
fplot(B)
xlim([ -0.01 0.01 ])
ylim([ -0.5 2.2 ])
grid
xlabel( 't' )
ylabel( 'B(t)' )
% временная осциллограмма отклика АЦП
syms t;
U = piecewise( 0 < t < 1, 5,1 < t < 2, 5, 2 < t < 3, 5, 3 < t < 4, 0, 4 < t < 5, 0, 5 < t < 6, 5, 6 < t < 7, 0, 7 < t < 8, 5, 8 < t < 9, 0 );
fplot( U, 'Linewidth',2 );
xlim([ 0 9 ]);
grid;
xlabel( 'tд' )
ylabel( 'U(t)' )
% реализация случайного процесса-------------------------------------------
syms t;
C = piecewise( 0 < t < 1, 1, 1 < t < 2, 1, 2 < t < 3, -1, 3 < t < 4, 1, 4 < t < 5, 1, 5 < t < 6, -1, 6 < t < 7, -1, 7 < t < 8, 1, 8 < t < 9, 1, 9 < t < 10, 1, 10 < t < 11, 1, 11 < t < 12, 1, 12 < t < 13, 1,13 < t < 14, -1, 14 < t < 15, -1, 15 < t < 16, -1, 16 < t < 17, 1, 17 < t < 18, -1 );
subplot(4,1,1), fplot( C, 'Linewidth',2 );
xlim([ 0 18 ]);
grid;
xlabel( 't' )
ylabel( 'c(t)' )
% прямоугольный импульс----------------------------------------------------
G = piecewise( 0 < t < 2, 1 );
subplot(4,1,2), fplot( G, 'Linewidth',2 );
xlim([ 0 18 ]);
ylim([ -1 1 ])
grid;
xlabel( 't' );
ylabel( 'g2(t)' );
% синфазный сигнал I(t)----------------------------------------------------
I = piecewise( 0 < t < 2, 1, 2 < t < 4, -1, 4 < t < 6, 1, 6 < t < 8, -1, 8 < t < 10, 1, 10 < t < 12, 1, 12 < t < 14, 1, 14 < t < 16, -1, 16 < t < 18, 1 );
subplot(4,1,3), fplot( I, 'Linewidth',2 );
xlim([ 0 18 ]);
ylim([ -1 1 ])
grid;
xlabel( 't' );
ylabel( 'I(t)' );
% квадратурный сигнал Q(t)-------------------------------------------------
Q = piecewise ( 0 < t < 2, 1, 2 < t < 4, 1, 4 < t < 6, -1, 6 < t < 8, 1, 8 < t < 10, 1, 10 < t < 12, 1, 12 < t < 14, -1, 14 < t < 16, -1, 16 < t < 18, -1 );
subplot(4,1,4), fplot( Q, 'Linewidth',2 );
xlim([ 0 18 ]);
ylim([ -1 1 ])
grid;
xlabel( 't' );
ylabel( 'Q(t)' );
% корреляционная функция случайного процесса C(t)--------------------------
syms t
B = piecewise ( t > (6.7750678 * 10^(-6)), 0, t < (-6.7750678 * 10^(-6)), 0, t <= (6.7750678 * 10^(-6)), 1 - (abs(t))/(6.7750678 * 10^(-6)), t >= (-6.7750678 * 10^(-6)), 1 - (abs(t))/(6.7750678 * 10^(-6)));
fplot( B, 'Linewidth', 2 )
xlim([ -0.00001 0.00001 ])
ylim([ 0 1 ])
grid
xlabel( 't' )
ylabel( 'B_C(t)' )
% спектральная плотность мощности C(t)-------------------------------------
syms w
G = 590399.9959 * (sin( w * 3.3875339 * 10^( -6 )))^2 / w^2 ;
fplot( G, 'Linewidth', 2 )
xlim([ -3*10^6 3*10^6 ])
ylim([ -0.0000002 0.0000069 ])
grid
xlabel( 'w' )
ylabel( 'G_C(w)' )
% корреляционная функция I(t), Q(t) и C(t)---------------------------------
syms t
B_C = piecewise ( t > (6.7750678 * 10^(-6)), 0, t < (-6.7750678 * 10^(-6)), 0, t <= (6.7750678 * 10^(-6)), 1 - (abs(t))/(6.7750678 * 10^(-6)), t >= (-6.7750678 * 10^(-6)), 1 - (abs(t))/(6.7750678 * 10^(-6)));
B_I_Q = piecewise ( t > (13.5501356 * 10^(-6)), 0, t < (-13.5501356 * 10^(-6)), 0, t <= (13.5501356 * 10^(-6)), 5 * (1 - (abs(t))/(13.5501356 * 10^(-6))), t >= (-13.5501356 * 10^(-6)), 5 * (1 - (abs(t))/(13.5501356 * 10^(-6))));
fplot( B_C, 'b--', 'Linewidth', 2 )
hold on
fplot( B_I_Q, 'Linewidth', 2 )
xlim([ -0.00002 0.00002 ])
ylim([ 0 5 ])
grid
xlabel( 't' )
ylabel( 'B_I(t), B_Q(t), В_С(t)' )
% спектральная плотность мощности I(t), Q(t) и C(t)------------------------
syms w
G_C = 590399.9959 * (sin( w * 3.3875339 * 10^( -6 )))^2 / w^2 ;
G_I_Q = 1475999.989 * (sin( w * 6.7750678 * 10^( -6 )))^2 / w^2 ;
fplot( G_C, 'b--', 'Linewidth', 2 )
hold on
fplot( G_I_Q, 'Linewidth', 2 )
xlim([ -2*10^6 2*10^6 ])
ylim([ -0.0000002 0.000068 ])
grid
xlabel( 'w' )