Файл: Курсовая работа по дисциплине Теория электрической связи (наименование учебной дисциплины согласно учебному плану).docx
Добавлен: 25.10.2023
Просмотров: 137
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
2) Частота дискретизации:
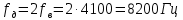
3) Число уровней квантования
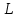 :
: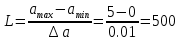
4) Мощность шума квантования:
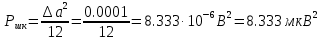
5) Минимальное число k двоичных разрядов, требуемое для записи в двоичной форме любого номера j из L 1 номеров уровней квантования:
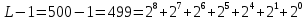
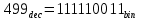
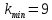
6) k-разрядное двоичное число, соответствующее заданному уровню квантования j:
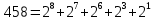
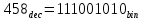
7) Временная осциллограммы отклика АЦП
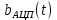 на заданный уровень квантования j в виде последовательности импульсов, сопоставляя единичным символам прямоугольные импульсы положительной полярности, а нулевым – нулевые напряжения:
на заданный уровень квантования j в виде последовательности импульсов, сопоставляя единичным символам прямоугольные импульсы положительной полярности, а нулевым – нулевые напряжения: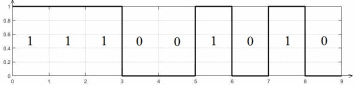
Рисунок 6 — Осциллограмма отклика АЦП на заданный уровень квантования
РАЗДЕЛ 3. КОДЕР
1) Заданы сделующие параметры свёрточного кодера:
Степень кодирования:
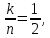
где k – количество информационных символов, поступающих на вход кодера в виде информационного блока;
n– количество кодовых символов, поступающих с выхода кодера в виде кодового блока.
Длина кодового ограничения:
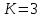
Векторы связи:
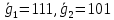
Импульсная характеристика h(k) задаётся информационной последовательностью
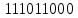 где k – номер тактового интервала.
где k – номер тактового интервала.Кодовое расстояние определяется сложением по модулю 2 импульсной характеристики и инормационной последовательности:
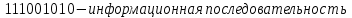
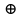
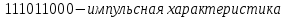
2) Структурная схема кодера:
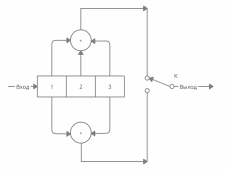
Рисунок 7 — Структурная схема кодера
3) Определение последовательности кодовых символов:
Таблица 2 — Определение последовательности кодовых символов
| Номер тактового интервала | Входной бит | Состояние регистра сдвига | Сумматор 1 | Сумматор 2 | Выходной дибит |
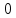 | - | 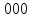 | - | - | - |
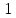 | 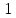 | 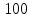 | 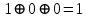 | 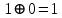 | 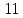 |
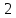 | 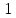 | 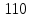 | 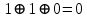 | 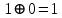 | 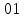 |
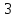 | 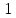 | 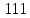 | 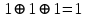 | 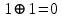 |  |
 |  |  | 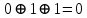 | 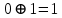 | 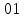 |
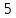 | 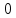 | 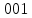 | 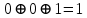 | 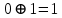 | 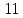 |
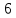 | 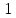 | 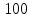 | 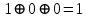 | 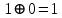 | 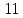 |
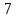 | 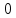 | 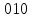 | 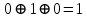 | 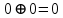 | 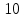 |
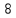 | 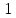 | 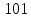 | 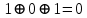 | 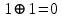 | 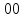 |
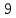 | 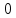 | 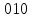 | 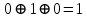 | 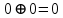 | 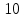 |
Таблица 3 — Информационные и закодированные символы
| Информационные символы (ИС) 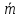 | 1 | 1 | 1 | 0 | 0 | 1 | 0 | 1 | 0 |
| Кодовые символы (КС) 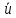 | 11 | 01 | 10 | 01 | 11 | 11 | 10 | 00 | 10 |
4) Решётчатая диаграмма свёрточного кодера от момента времени
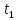 до момента времени
до момента времени 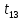 и путь, соответствующий полученному кодовому символу:
и путь, соответствующий полученному кодовому символу: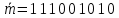

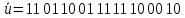
Рисунок 8 — Решётчатая диаграмма свёрточного кодера
РАЗДЕЛ 4. ФОРМИРОВАТЕЛЬ МОДУЛИРУЮЩИХ СИМВОЛОВ
1) Сигнальное созвездие для квадратурной фазовой модуляции КФМ – 4:
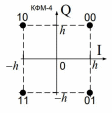
Рисунок 9 — Сигнальное созвездие для КФМ - 4
2) Реализация c(t) случайного процесса C(t), реализации i(t) и q(t) на выходе блока ФМС:
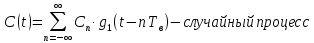
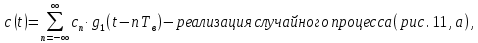
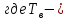 длительность двоичного символа
длительность двоичного символа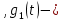 прямоугольный импульс длительностью
прямоугольный импульс длительностью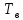 ,
,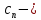 численный коэффициент, являющийся реализацией случайной величины
численный коэффициент, являющийся реализацией случайной величины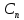 на n-интервале
на n-интервале 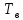 .
.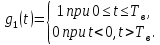
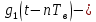 прямоугольный импульс такой же формы, как
прямоугольный импульс такой же формы, как 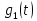 (рис. 11, б), но сдвинутый вправо относительно импульса
(рис. 11, б), но сдвинутый вправо относительно импульса 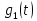 на величину
на величину 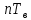 , если
, если 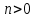 , или влево, если
, или влево, если 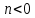 .
.На выходах блока ФМС для КФМ-4 (рис. 10) также появляются сигналы
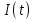 и
и 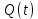 (рис. 11, в, г), представленные в виде формул:
(рис. 11, в, г), представленные в виде формул: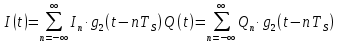
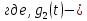 прямоугольный импульс длительностью
прямоугольный импульс длительностью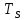 ,
, 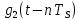
аналлогично
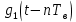 ,
,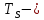 длительность модулирующих сигналов
длительность модулирующих сигналов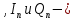 независимые случайные величины, которые согласно сигнальному созвездию принимают два дискретных значения
независимые случайные величины, которые согласно сигнальному созвездию принимают два дискретных значения 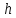 и
и 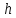 , с вероятностью
, с вероятностью 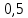 каждое:
каждое: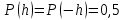
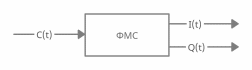
Рисунок 10 — Формирователь модулирующих символов
Определим длительность двоичного символа
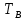 на выходе кодера:
на выходе кодера: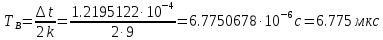
и длительность модулирующих сигналов:
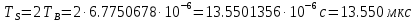
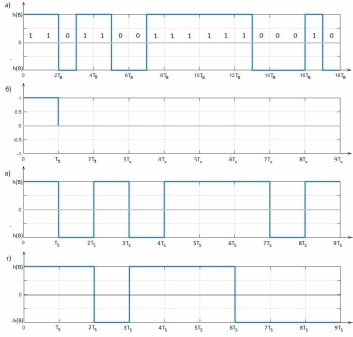
Рисунок 11 — а) реализация
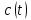 случайного процесса
случайного процесса 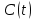 , формируемого с выхода блока свёрточного кодера; б) осциллограмма прямоугольного импульса
, формируемого с выхода блока свёрточного кодера; б) осциллограмма прямоугольного импульса 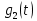 длительностью
длительностью 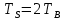 ; в) реализация
; в) реализация 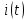 случайного процесса
случайного процесса 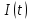 на выходе блока ФМС; г) реализация
на выходе блока ФМС; г) реализация 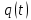 случайного процесса
случайного процесса 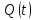 на выходе блока ФМС
на выходе блока ФМС3) Корреляционная функция
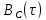 (рис. 12) и спектральная плотность мощности
(рис. 12) и спектральная плотность мощности 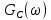 (рис. 13) входного случайного процесса
(рис. 13) входного случайного процесса 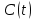 (сигнала на входе ФМС):
(сигнала на входе ФМС):