Файл: Курсовая работа по дисциплине Теория электрической связи (наименование учебной дисциплины согласно учебному плану).docx

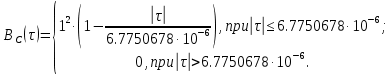
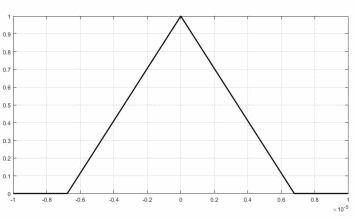
Рисунок 12 — График корреляционной функция случайного процесса




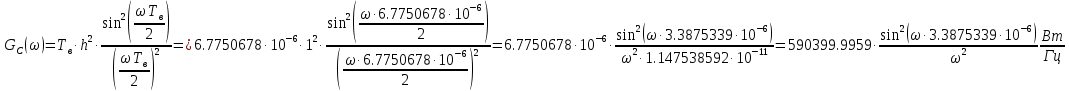
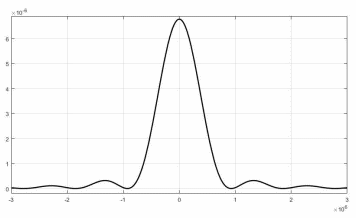
Рисунок 13 — Спектральная плотность мощности 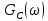случайного процесса
3) Корреляционные функции 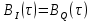(рис. 14) и спектральные плотности мощности 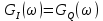(рис. 15):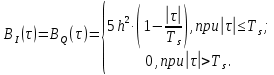







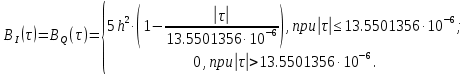
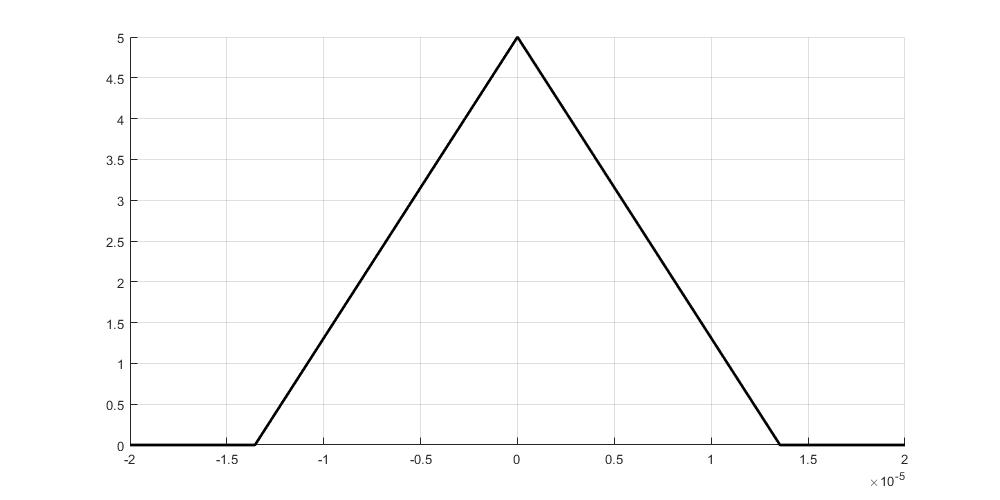
Рисунок 14 — График корреляционных функций




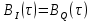
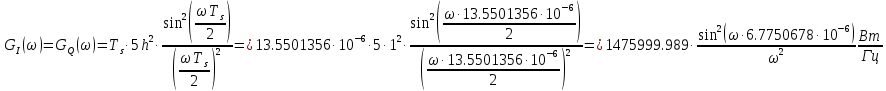
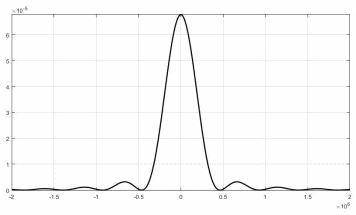
Рисунок 15 — Спектральные плотности мощности
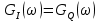
4) Сравнение корреляционных функций 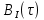, , 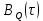(рис. 16) и спектральных плотностей мощности 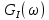, , 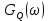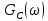синфазного и квадратурного сигналов (сигналов на выходе ФМС) (рис. 17):

Отличие 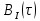от корреляционной функции 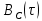проявляется в том, что вместо множителя

---

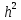используется множитель 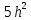и вместо параметра используется параметр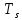



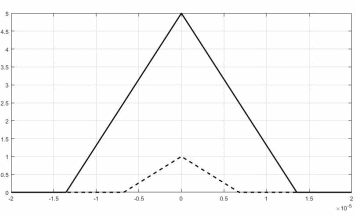
Рисунок 16 — Графики корреляционных функций 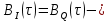сплошлая линия 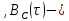пунктирная линия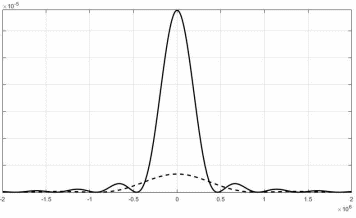


Рисунок 17 — Спектральные плотности мощности 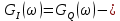сплошлая линия 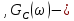пунктирная линия

6) Анализ графиков (рис. 16, 17).

Корреляционные функции сигналов на выходе блока ФМС в 2 раза шире, чем корреляционные функции на входе. Это объясняется увеличением длительности интервала .

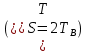Для того, чтобы объяснить сужение спектра, обратимся к преобразованию Фурье.
Возьмём функцию, зависящую от величины 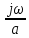и выразим через прямое преобразование Фурье: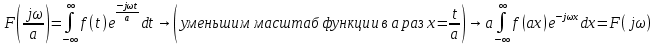



Уменьшив масштаб, получаем функцию зависящую от 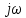. Таким образом, подставляя вместо 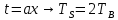, получаем сужение частотного спектра в 2 раза.

---

РАЗДЕЛ 5. МОДУЛЯТОР

Подраздел 5.1. Сглаживающий формирующий фильтр

1) Структурная схема модулятора в составе ЦСС (рис. 18):

В состав модулятора структурной схемы цифровой системы связи (ЦСС) между блоками формирователя модулирующих символов (ФМС) и перемножителями входят сглаживающие формирующие фильтры (СФФ), необходимые для оптимизации ЦСС в отношении межсимвольной помехи, а также инвертор и сумматор, на выходе которого получаем сигнал заданного вида модуляции.



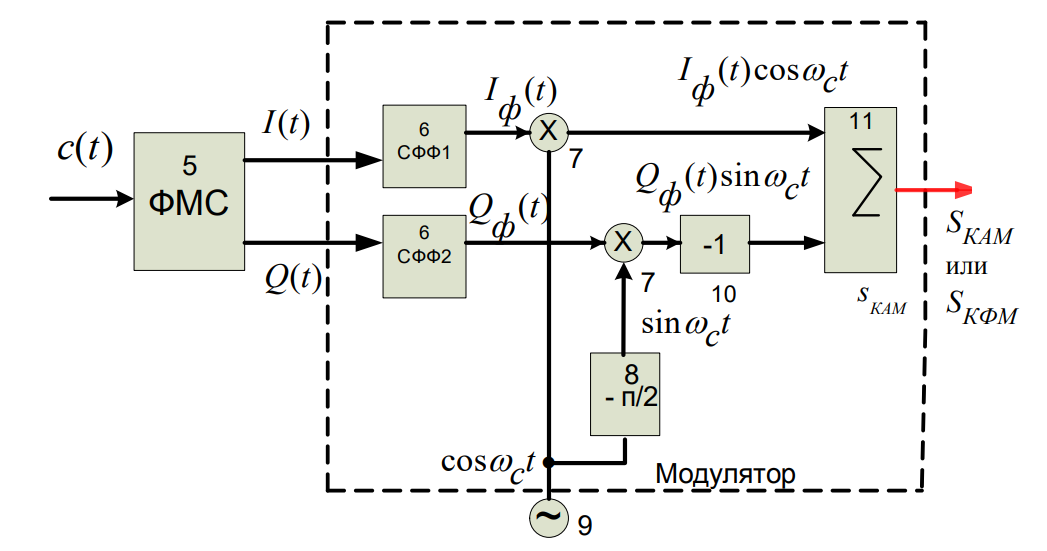
Рисунок 18 — Расположение блоков СФФ в схеме цифровой системы связи с квадратурной модуляцией

2) Сигнал 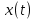со «спектром приподнятого косинуса» (импульса Найквиста) (рис. 19) и его спектральной плотности 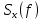(рис. 20) для значений коэффициента сглаживания :




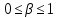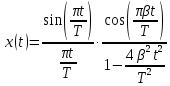
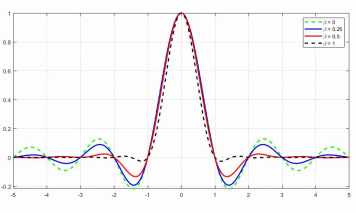
Рисунок. 19 — Импульсы Найквиста при





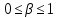
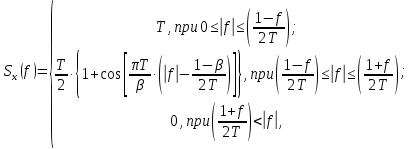
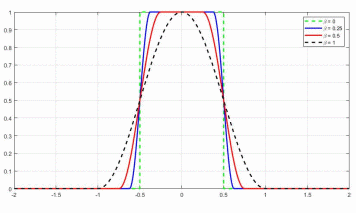
Рисунок 20 — Спектральные плотности импульсов Найквиста при
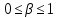
Для простоты масштабирования T принимаем за 1.
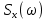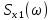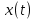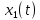3) Графики спектральных плотностей и (рис. 21) сигналов и , где 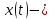импульс Найквиста при коэффициенте сглаживания 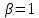; 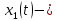импульс со спектральной плотностью :

---

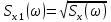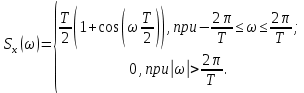
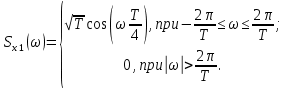
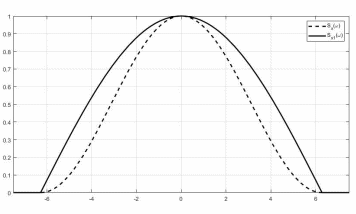
Рисунок 21 — Спектральные плотности и
4) Импульсы и 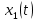(рис. 22):

Для того, чтобы определить импульс , воспользуемся обратным преобразованием Фурье от спектральной плотности 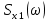с интервалами интегрирования :



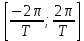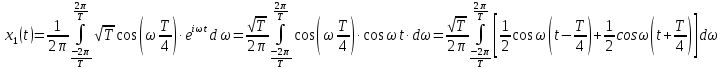
После элементарных преобразований окончательно определим искомый сигнал :





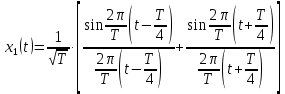
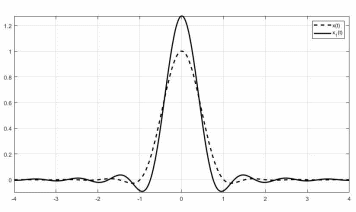
Рисунок 22 — Графики импульсов и
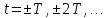Значения импульса Найквиста в моменты времени равны нулю, а значения импульса в эти же моменты времени отличаются от нуля.

Величина главного максимума импульса равна единице, а величина главного максимума зависит от параметра 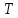и равна .

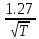5) Cлучайные процессы 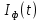и :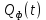

В сигнал на выходе сумматора КФМ входят случайные процессы:

---

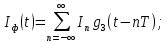
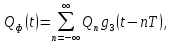
где 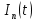и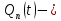 независимые случайные величины, принимающие известные дискретные значения с заданными вероятностями, 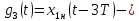детерминированный импульс, спектральная плотность которого выражается через спектральную плотность импульса Найквиста.

6) Корреляционные функции (рис. 23) и спектральные плотности мощности случайных процессов и (рис. 24):
Корредяционные функции случайных процессов 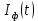и :



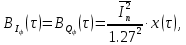
где 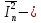математическое ожидание для КФМ – 4 равное , 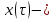импульс Найквиста при .



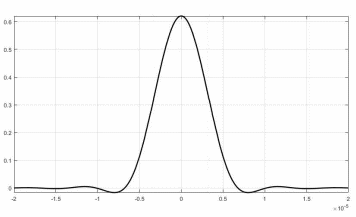
Рисунок 23 — График корредяционных функций 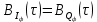случайных процессов 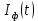и
Максимумы функций находятся в точке ( 0 ; ).

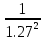Cпектральные плотности мощности случайных процессов и :




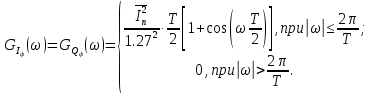
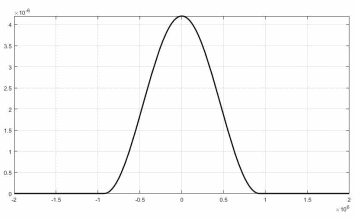
Рисунок 24 — График спектральных плотностей мощности 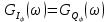случайных процессов 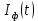и

---