1.5 Сравнение полученных результатов

Рассчитаем скорость и ускорение точки S₂





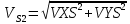
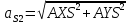
Проведем расчет погрешностей :









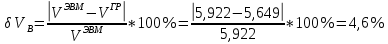
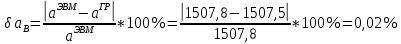
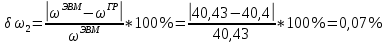
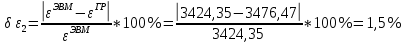
Результат для каждого положения сведем в таблицу 4.
Таблица 4 – Анализ полученных значений для положения №12

	VB, м/с	aB, м/с2	ω2, с-1	ε2, с-2
ЭВМ	5,922	1507,8	40,43	3424,35
Графика (план скоростей)	5,649	1507,5	40,4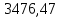
δ, %	4,6	0,02	0,07	1,5

4 Синтез зубчатого механизма

4.1 Геометрический расчет передачи внешнего зацепления [ 5 ]

Чтобы спроектировать передачу с максимальной износостойкостью и коэффициентом перекрытия 1,2 ,по блокирующему контуру определяем коэффициенты смещения :

x₁ = 0.83 и x₂ = 0.39.

Угол зацепления в паре:

,

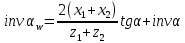Где угол станочного зацепления α = 20˚ ,

и inv α = inv 20˚ = 0.0149.

,

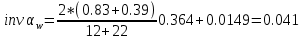α_w = 27 (α_w находится по таблице 4.14).

Радиусы делительных окружностей:

r = 0.5mz,

где m – модуль,

z – число зубьев.

r₁ = 0.5*16*12 = 96 (мм),

r₂ = 0.5*16*22 = 176 (мм),

Радиусы начальных окружностей:

r_w = r·cosα/cosα_w,

r_w1 = 96*cos20/ cos27= 101,25 (мм),

r_w

---

₂ = 176*cos20/cos27 = 185.6 (мм),

---

Межосевое расстояние:

a_w = r_w1 + r_w2 ,

a_w = 101.25 + 185.6 = 286.85 (мм),

Радиусы основных окружностей:

r_b = r*cosα,

r_b1 = 96*cos20 = 90.21 (мм),

r_b2 = 176*cos20 = 165.39 (мм),

Радиусы окружностей впадин:

r_f = r – h^*_am – c^*m + x*m,

где h^*_a – коэффициент высоты головки зуба (h^*_a = 1),

с^* - коэффициент радиального зазора (с^* = 0.25),

r_f1 = 96 – 1*16 – 0.25*16 + 0.83*16 = 89.28 (мм),

r_f2 = 176 – 1*16 – 0.25*16 + 0.39*16 = 162.24 (мм),

Радиусы окружностей вершин:

r_a1 = a_w – r_f2 – c^*m,

r_a2 = a_w – r_f1 – c^*m,

r_a1 = 286.85 – 162.24 – 0.25*16 = 120.61 (мм),

r_a2 = 286.85 –89.28 – 0.25*16 = 193.57 (мм),

Высота зуба:

h = r_a – r_f ,

h = 120.61 – 89.28 = 31.33 (мм),

h = 193.57 – 162.24 = 31.33 (мм),

Шаг по делительной окружности:

P = πm

P = 3.14*16 = 50.24 (мм),

Толщина зуба по делительной окружности:

S = m(0.5π + 2xtgα),

S₁ = 16*(0.5*3.14 + 2*0.83*tg20) = 34.79 (мм),

S₂ = 16*(0.5*3.14 + 2*0.39*tg20) = 29.66 (мм),

Ширина впадин по делительной окружности:

e = P – S,

e₁ = 50.24 – 34.79 = 15.45 (мм),

e₂ = 50.24 – 29.66 = 20.58 (мм),

4.2 Качественные показатели зацепления

Коэффициент перекрытия:

,



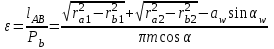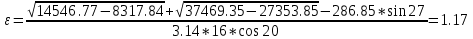
Коэффициенты относительного скольжения зубьев:

,

,

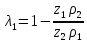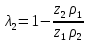где

ρ₁₍₂₎ – радиусы кривизны профилей зубьев шестерни и колеса, соответственно.

Формулы для их расчета приведены в таблице 11.

Таблица 11

Точка	Расчетная формула	Радиусы кривизны,мм
N1	ρ1 = 0, ρ2 = awsinαw = C	ρ1 = 0, ρ2 = 130.23,
A	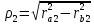, ρ1 = C – ρ2,	ρ2 = 100.57, ρ1 = 29.66,
P	ρ1 = rw1sinαw, ρ2 = rw2sinαw,	ρ1 = 45.97, ρ2 = 84.26,
B	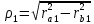, ρ2 = C – ρ1,	ρ1 = 80.06, ρ2 = 50.17,
N2	ρ1 = C, ρ2 = 0,	ρ1 = 130.23, ρ2 = 0,

---

ρ_пр – приведенный радиус кривизны.

,

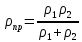Результаты расчета сведены в таблицу 12.

Таблица 12

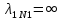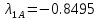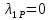, , .0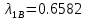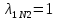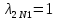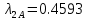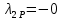002, , ,

, , .0002, , ,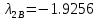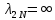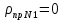

(мм), (м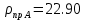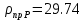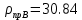м), (мм),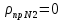 (мм), (мм),

Коэффициент удельного давления (рассчитывается для тех же точек линии зацепления):

ϋ= m/ρ_пр,

Результаты сведены в таблицу 13

Таблица 13

ϋN1 = ∞, ϋВ = 0.6987, ϋP = 0.5379, ϋА = 0.5188, ϋN2 = ∞,

4.3 Синтез планетарного механизма

Задача кинематического синтеза планетарного механизма состоит в определении чисел зубьев колес при заданной кинематической схеме и передаточном отношении. Наличие

нескольких сателлитов налагает ряд дополнительных условий, которые необходимо учитывать при проектировании: условие соосности, условие сборки и условие соседства.

Передаточное отношение ,

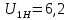Модуль колес редуктора m = 3 (мм),

Число саттелитов K = 3,

Тип редуктора: редуктор Джеймса (A-I).

---

Для заданного типа редуктора выбираем коэффициенты: a = -1, b = 1, c = -1.

Записываем соотношения для чисел зубьев редуктора:

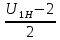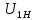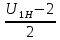z₁ : z₂ : z₃ : z₄ : j = 1: : ( -1) : (219)

z1:z2:z3:j = 1:(62/10-2)/2:(62/10-1):(62/10-2)/3 = 1:(62/10-20/10)/2:(62/10-10/10):

(62/10-20/10)/3 = 1:42/20:52/10:42/30 = 1:21/10:52/10:42/30.

Домножаем на 30:

z1:z2:z3:j = 30:63:156:42

Коэффициент j = 42, т.е. получился целым числом, значит можем принять данные

Значения чисел зубьев для колес: z1 = 30; z2 = 63; z3 = 156.

Радиусы начальных окружностей колес (колеса не корригированные):

r1 = 0.5*m*z1 = 0.5*3*30 = 45.000 (мм)

r2 = 0.5*m*z2 = 0.5*3*63 = 94.500 (мм)

r3 = 0.5*m*z3 = 0.5*3*156 = 234.000 (мм)

Выполняем проверку на соосность:

r1+b*r2 = r3+c*r2

45+1*94.5 = 234-1*94.5

139.5 = 139.5 верно, условие выполняется

Выполняем проверку на сборку ( для редуктора Джеймса данную проверку можно не

выполнять, он соберется в любом случае):

L = z3/K-z1/K = 156/3-30/3 = 42

Коэффициент L получился целым, т.е. условие выполняется.

Проверяем условие соседства:

(z1+b*z2)*sin(π/k)-z2 > 2*ha

(30+1*63)*sin(3.14/3)-63 > 2*1

17.538 > 2 верно, условие выполняется

(z3+c*z2)*sin(π/k)-z2 > ha

(156-1*63)*sin(3.14/3)-63 > 2*1

17.538 > 2 верно, условие выполняется

Результат:

z1 = 30	r1 = 45.000 мм
z2 = 63	r2 = 94.500 мм
z3 = 156	r3 = 234.000 мм

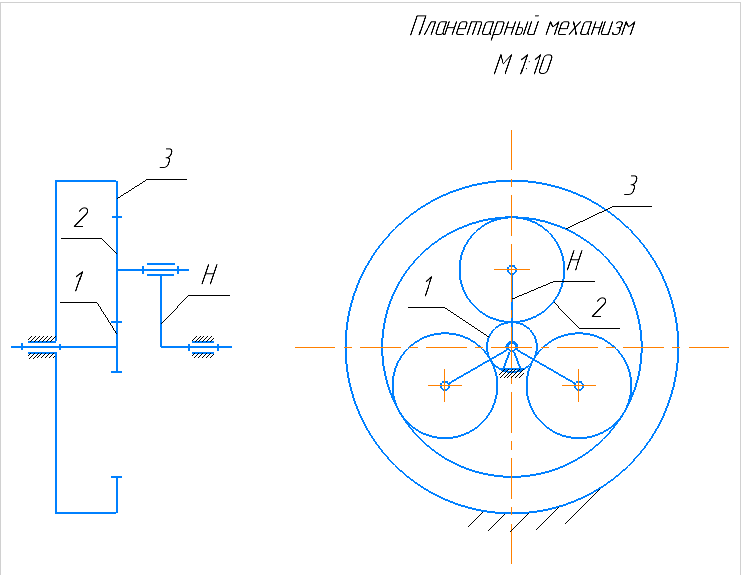
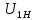	m, мм	k	z1	z2	z3
6.2	3	3	30	63	156

1. 
   Силовой расчет двигателя внутреннего сгорания
   

Дано:

---

Смотрите также файлы

• Преподаватель медицинского вуза вчера, сегодня, завтра.odt

• Взаимосвязь инфляции и безработицы классическая и вертикальная кривые Филипса..docx

• Ответ в предложенном варианте мы наблюдаем конформность. Василий, не зная начальника, имеет не лучшее мнение о нём и его характере, потому что в коллективе, в который он попал выстроены такие установки.docx

• Конспект общеразвивающих упражнений с предметами для детей 34 лет.doc

• Реферат (вид работы) Тема Нравственная культура экономиста этические и нравственные основы формирования антикоррупционного поведения.docx