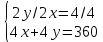Добавлен: 25.10.2023
Просмотров: 73
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
, меньше, чем площадь треугольника, ограниченного бюджетной линией 
.3. Введение администрацией региона потоварной субсидии на товар
в размере 
руб. привело к тому, что фактическая цена товара для потребителя стала равняться: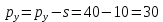
руб.Следовательно, при сохранении налога на товар
бюджетное ограничение принимает вид:
;
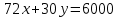,координата точки пересечения бюджетной линии с осью ординат равна:
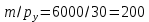единиц товара ,а угол ее наклона:
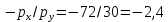.Соответствующее изменение положения линии бюджетного ограничения относительно первоначальной ситуации показано на рисунке 2.4.
Рис. 2.4. Бюджетное множество потребителя после установления
налога на товар
и субсидии на товар Вывод: количество доступных потребителю товарных наборов при одновременном влиянии налога и субсидии возросло, т.к. прирост в доступности товара
, составивший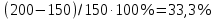 
, оказался больше, чем сокращение доступности товара , равное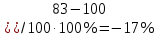 
.4. Введение магазином системы скидок на приобретение товара
означает, что товар стал для данного покупателя более доступным. Если бы предоставление скидки с цены товара было обусловлено необходимостью приобрести его количество, превышающее некоторый минимум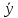 
, то линия бюджетного ограничения потребителя имела бы вид ломаной кривой, которая математически описывалась бы следующей системой уравнений: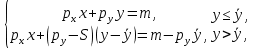
где
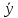– минимальное количество покупок товара , при превышении которого начинает действовать система скидок;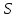 
– величина скидки за единицу товара , руб.Графически бюджетное ограничение было бы представлено рисунком 2.5.
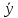
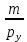
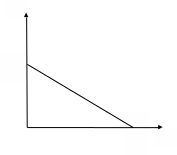
Рис. 2.5. Бюджетное множество потребителя после введения
системы скидок на товар
Однако, т.к. скидка начинает действовать при осуществлении первой же покупки (параметр
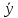
не задан), то линия бюджетного ограничения будет характеризоваться уравнением:
;
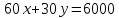,где
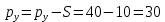руб.;точкой пересечения с осью ординат:
единиц товара ,и углом наклона:
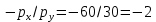.Соответствующее изменение положения линии бюджетного ограничения относительно первоначальной ситуации показано на рисунке 2.6.
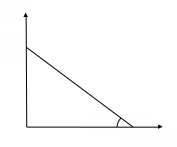
Рис. 2.6. Бюджетное множество потребителя с учетом фактического действия системы скидок на товар
Вывод: количество доступных потребителю товарных наборов при введении скидки на товар
увеличится.Практическое задание 3
Тема 2. Поведение потребителя: бюджетные ограничения и выбор
Задача
Известно, что для потребительского набора
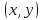функция полезности потребителя задана уравнением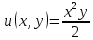 
. Общий доход, которым располагает потребитель, составляет
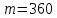ден. ед. Цена товара – 
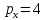ден. ед., цена товара – 
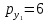ден. ед. Предположим, что цена товара понижается до уровня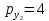 
ден. ед.Осуществите следующие действия:
- выпишите уравнение бюджетной линии и постройте график бюджетного ограничения;
- определите эффект замены (по Хиксу);
- определите эффект дохода (по Хиксу);
- определите общий эффект (по Хиксу);
- охарактеризуйте данный товар (нормальный, инфериорный, товар Гиффена).
Решение
Бюджетное ограничение по заданным значениям
и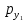 
принимает вид:
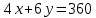.Оптимальный выбор потребителя представлен на рисунке 3.1.
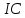
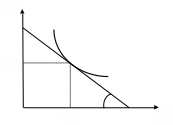
Рис. 3.1. Потребительский выбор
Для расчета величины эффектов замещения и дохода прежде всего необходимо найти параметры внутреннего равновесия потребителя до и после снижения цены товара
.
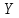
Первоначальную оптимальную комбинацию благ
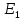можно найти из решения следующей системы уравнений:
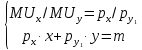.Первое равенство представляет собой условие максимизации полезности потребителя при равенстве угла наклона касательной к кривой безразличия в точке оптимума (показатель предельной нормы замещения товаром
товара 
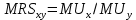) углу наклона бюджетной линии 
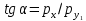в этой же точке. Второе равенство – уравнение бюджетного ограничения потребителя 
.Находим функции предельных полезностей товаров
и как условную производную функции совокупной полезности по соответствующему товару: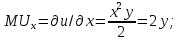
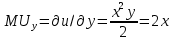.Подставляем известные значения в систему уравнений:
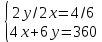.Из первого равенства:
;
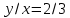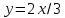.Подставляем в бюджетное уравнение:
;
;
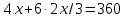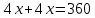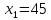ед.Тогда
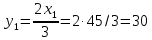ед.После понижения цены товара
до 
ден. ед. оптимум потребителя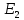 
описывается системой уравнений вида:
;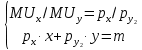