Добавлен: 25.10.2023
Просмотров: 71
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
– коэффициент угла наклона функции спроса.
Следовательно, функция спроса на продукцию монополиста может быть представлена уравнением:
;
.
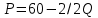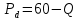Определяем цену, которую назначит монополист на свою продукцию, подставляя в полученную функцию спроса величину оптимального выпуска:
.
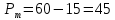Эластичность в точке оптимума монополиста рассчитаем по формуле точечной эластичности спроса по цене:
,
где
– коэффициент эластичности спроса на благо по его цене;
– первая производная функции спроса по параметру цены 
; 
– уравнение кривой спроса.
Представим функцию спроса в виде прямой:
.
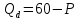Находим производную функции спроса по :
.
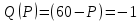Тогда эластичность спроса по цене в точке максимизации монополистом своей прибыли равна:
.
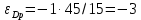Практическое задание 6
Тема 5. Общее равновесие и экономическая эффективность
Задача
Предположим, что издержки по вывозу мусора с территории двух районов составляют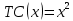
, где 
– площадь территории. Проведенные исследования выявили, что предпочтения всех жителей 1-го района принимают вид функции полезности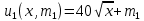 
, а предпочтения всех жителей 2-го района – 
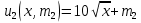, где 
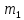и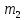 
– потребление агрегированного блага (вывоз мусора) всеми жителями соответствующих районов.
Найдите Парето-эффективное значение вывоза мусора с районов. Изобразите решение задачи на графике.
Решение
Поскольку функции полезности потребителей заданы как квазилинейные, то условие определения Парето-оптимального значения производства общественного блага принимает вид:
,
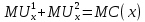где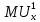
– предельная полезность общественного блага для первой группы потребителей; 
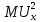– предельная полезность общественного блага для второй группы потребителей; 
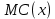– предельные издержки производства общественного блага.
Находим предельные полезности:
;
.
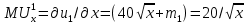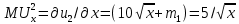Определяем функцию предельных затрат:
.
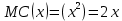Подставляем найденные выражения в условие Парето-оптимальности:
;
;
;
.
;
.
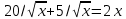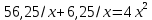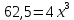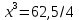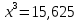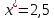Таким образом, Парето-эффективное значение вывоза мусора с районов составляет .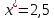
Представим решение графически (см. рисунок).
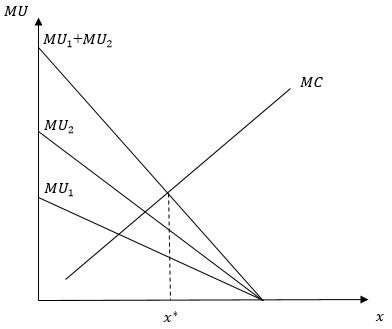
Рис. – Определение Парето-эффективного значения производства общественного блага
Следовательно, функция спроса на продукцию монополиста может быть представлена уравнением:
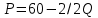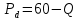; .Определяем цену, которую назначит монополист на свою продукцию, подставляя в полученную функцию спроса величину оптимального выпуска:
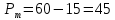.Эластичность в точке оптимума монополиста рассчитаем по формуле точечной эластичности спроса по цене:
,где
– коэффициент эластичности спроса на благо по его цене; – первая производная функции спроса по параметру цены ; – уравнение кривой спроса.Представим функцию спроса в виде прямой:
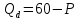.Находим производную функции спроса по
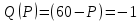: .Тогда эластичность спроса по цене в точке максимизации монополистом своей прибыли равна:
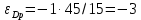.Практическое задание 6
Тема 5. Общее равновесие и экономическая эффективность
Задача
Предположим, что издержки по вывозу мусора с территории двух районов составляют
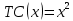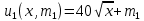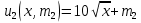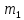, где – площадь территории. Проведенные исследования выявили, что предпочтения всех жителей 1-го района принимают вид функции полезности , а предпочтения всех жителей 2-го района – , где и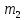
– потребление агрегированного блага (вывоз мусора) всеми жителями соответствующих районов.
Найдите Парето-эффективное значение вывоза мусора с районов. Изобразите решение задачи на графике.
Решение
Поскольку функции полезности потребителей заданы как квазилинейные, то условие определения Парето-оптимального значения производства общественного блага принимает вид:
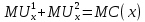,где
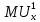– предельная полезность общественного блага для первой группы потребителей; 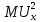– предельная полезность общественного блага для второй группы потребителей; 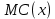– предельные издержки производства общественного блага.Находим предельные полезности:
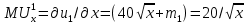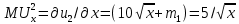; .Определяем функцию предельных затрат:
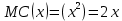. Подставляем найденные выражения в условие Парето-оптимальности:
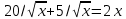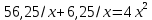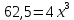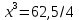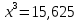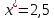; ; ; . ; .Таким образом, Парето-эффективное значение вывоза мусора с районов составляет
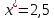.Представим решение графически (см. рисунок).
Рис. – Определение Парето-эффективного значения производства общественного блага