Добавлен: 25.10.2023
Просмотров: 70
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
.
Из первого равенства:
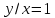 ;
;
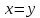 .
.
Подставляем в бюджетное уравнение:
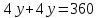 ;
;
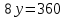 ;
;
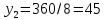 ед.
ед.
Тогда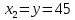 ед.
ед.
Т.к. функция полезности в данном случае является функцией Кобба-Дугласа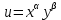 , то данные вычисления можно было значительно упростить, воспользовавшись «правилом долей»:
, то данные вычисления можно было значительно упростить, воспользовавшись «правилом долей»:
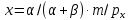 ,
,
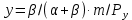 ,
,
где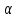 и
и 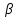 – коэффициенты эластичности полезности по потреблению товаров
– коэффициенты эластичности полезности по потреблению товаров  и
и  , соответственно;
, соответственно;
 – бюджет покупателя;
– бюджет покупателя;
 – цена товара
– цена товара  ;
;
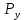 – цена товара
– цена товара  .
.
Для первоначального равновесия:
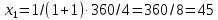 ед.,
ед.,
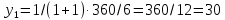 ед.
ед.
Для последующего равновесия:
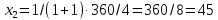 ед.,
ед.,
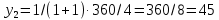 ед.
ед.
Изменение цены одного из товаров, входящих в потребительский набор, вызывает появление общего эффекта от этого изменения, который может быть разложен на эффект замены (замещения).
Эффект замены (замещения) – это часть общего эффекта изменения цены товара, вызванная изменением относительной привлекательности этих и других товаров.
Эффект дохода – это часть общего эффекта изменения цены товара, вызванная изменением реальной покупательной способности дохода потребителя.
Общий эффект – сумма эффектов дохода и замещения.
Определим указанные эффекты по методу Хикса.
Согласно подходу Хикса, после изменения цены товара получаемая потребителем полезность не изменится, если при новых ценах он может себе позволить приобрести товарный набор с тем же уровнем полезности, что и первоначальный потребительский набор:
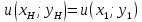 ,
,
где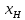 ,
, 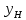 – это оптимальные количества товаров
– это оптимальные количества товаров  и
и  во вспомогательной точке равновесия потребителя (точке Хикса)
во вспомогательной точке равновесия потребителя (точке Хикса) 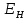 .
.
Следовательно, вспомогательная бюджетная линия (линия Хикса) должна иметь тот же угол наклона, что и бюджетная линия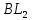 (описывающаяся уравнением
(описывающаяся уравнением 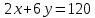 ), но являться касательной к первоначальной кривой безразличия потребителя
), но являться касательной к первоначальной кривой безразличия потребителя 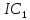 .
.
Тогда система уравнений, из решения которой можно определить вспомогательный товарный набор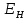 выглядит следующим образом:
выглядит следующим образом:
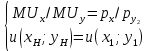 ;
;
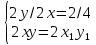 .
.
Первое равенство преобразуется в:
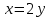 .
.
Подставляем полученное выражение и известные значения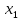 и
и 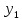 во второе выражение:
во второе выражение:
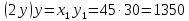 ;
;
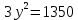 ;
;
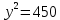 ;
;
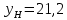 ед.
ед.
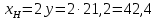
ед.
Следовательно, эффект замены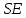 по Хиксу составляет:
по Хиксу составляет:
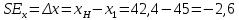 ;
;
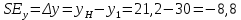 .
.
Эффект дохода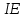 по Хиксу равен:
по Хиксу равен:
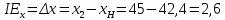 ;
;
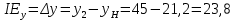 .
.
Общий эффект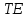 , рассчитанный по изменениям количеств товаров
, рассчитанный по изменениям количеств товаров  и
и  :
:
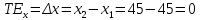 ;
;
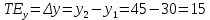 .
.
Проверяем, определяя общий эффект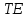 , как сумму эффектов дохода и замещения:
, как сумму эффектов дохода и замещения:
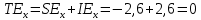 ;
;
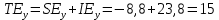 .
.
Вывод: поскольку снижение цены товара вызвало повышенный спрос, то данный товар является нормальным (товаром высокого качества).
вызвало повышенный спрос, то данный товар является нормальным (товаром высокого качества).
Практическое задание 4
Тема 3. Поведение производителя и конкуренция
Задачи
Технологическая норма замещения факторов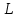 и
и 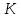 равна
равна 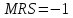 . Предположим, что фирма готова произвести тот же самый объем выпуска, но сократить использование фактора
. Предположим, что фирма готова произвести тот же самый объем выпуска, но сократить использование фактора 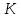 на
на 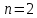 единицы. Сколько дополнительных единиц фактора
единицы. Сколько дополнительных единиц фактора 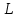 потребуется фирме?
потребуется фирме?
Решение
Формула расчета технологической нормы замещения факторов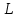 и
и 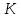
имеет вид:
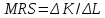 ,
,
где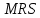 – технологическая норма замещения факторов
– технологическая норма замещения факторов  и
и  ;
;
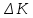 – изменение количества применяемого в производственном процессе фактора
– изменение количества применяемого в производственном процессе фактора  ;
; 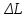 – изменение количества применяемого в производственном процессе фактора
– изменение количества применяемого в производственном процессе фактора  .
.
Выражаем из этой формулы изменение количества фактора :
:
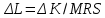 ;
;
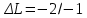 ;
;
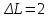 единицы фактора
единицы фактора  .
.
Графическое решение представлено на рисунке.
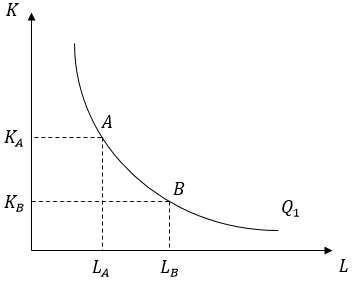
Рис. Изменение количества фактора при сокращении использования фактора
при сокращении использования фактора 
Из рисунка следует, что если фирма желает остаться на прежней изокванте (линии равного выпуска)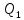 , то при сокращении использования фактора
, то при сокращении использования фактора  (смещении из точки
(смещении из точки 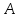 в точку
в точку 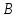 ) она должна вовлечь в производство дополнительное количество фактора
) она должна вовлечь в производство дополнительное количество фактора  .
.
Вывод: расчеты показывают, что количество использования фактора необходимо увеличить на 2 единицы.
необходимо увеличить на 2 единицы.
Практическое задание 5
Тема 4. Рыночные структуры и стратегия поведения
Задачи
1. Предположим, что на рынке действуют две фирмы, функции общих издержек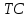 заданы уравнениями:
заданы уравнениями: 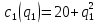 и
и 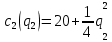 . Рыночный спрос описывается функцией:
. Рыночный спрос описывается функцией:
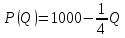 ,
,
где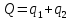 .
.
Определите объем продаж, который будет у каждой фирмы, и цену, которая установится на рынке, если:
- фирмы конкурируют по Курно;
- фирмы конкурируют по Бертрану;
- фирмы конкурируют по сценарию Штакельберга.
Изобразите решение на графике.
Решение
В модели некооперированной дуополии Курно каждый дуополист исходит из предположения, что его соперник не изменит своего выпуска в ответ на его собственное решение. Это значит, что, принимая его, дуополист руководствуется стремлением к максимизации своей прибыли, полагая выпуск другого дуополиста заданным.
В данной модели состояние устойчивого равновесия в отрасли достигается в точке пересечения кривых реагирования дуополистов – точке равновесия Курно-Нэша. Кривые реагирования (кривые наилучшего ответа) – это множества точек наивысшей прибыли, которую может получить один из дуополистов при данной величине выпуска другого.
Представим функцию рыночного спроса в виде:
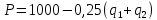 .
.
Выразим функции прибыли каждого из дуополистов:
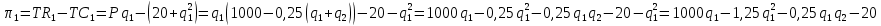 ;
;
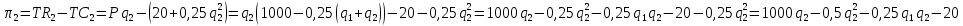 .
.
Определим максимум полученных функций, найдя их первую производную и приравняв ее к 0:
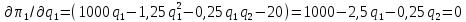 ;
;
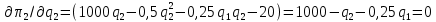 .
.
Запишем уравнения кривых реагирования каждого из дуополистов, представив выпуск одного через выпуск другого.
Кривая реагирования дуополиста 1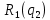 имеет вид:
имеет вид:
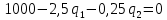
Из первого равенства:
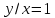 ;
;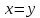 .
.Подставляем в бюджетное уравнение:
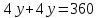 ;
;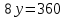 ;
;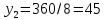 ед.
ед.Тогда
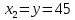 ед.
ед.Т.к. функция полезности в данном случае является функцией Кобба-Дугласа
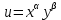 , то данные вычисления можно было значительно упростить, воспользовавшись «правилом долей»:
, то данные вычисления можно было значительно упростить, воспользовавшись «правилом долей»: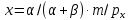 ,
,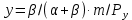 ,
,где
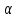 и
и 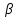 – коэффициенты эластичности полезности по потреблению товаров
– коэффициенты эластичности полезности по потреблению товаров  и
и  , соответственно;
, соответственно; – бюджет покупателя;
– бюджет покупателя; – цена товара
– цена товара  ;
;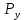 – цена товара
– цена товара  .
.Для первоначального равновесия:
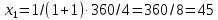 ед.,
ед.,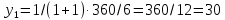 ед.
ед.Для последующего равновесия:
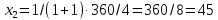 ед.,
ед.,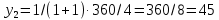 ед.
ед.Изменение цены одного из товаров, входящих в потребительский набор, вызывает появление общего эффекта от этого изменения, который может быть разложен на эффект замены (замещения).
Эффект замены (замещения) – это часть общего эффекта изменения цены товара, вызванная изменением относительной привлекательности этих и других товаров.
Эффект дохода – это часть общего эффекта изменения цены товара, вызванная изменением реальной покупательной способности дохода потребителя.
Общий эффект – сумма эффектов дохода и замещения.
Определим указанные эффекты по методу Хикса.
Согласно подходу Хикса, после изменения цены товара получаемая потребителем полезность не изменится, если при новых ценах он может себе позволить приобрести товарный набор с тем же уровнем полезности, что и первоначальный потребительский набор:
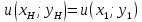 ,
,где
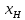 ,
, 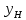 – это оптимальные количества товаров
– это оптимальные количества товаров  и
и  во вспомогательной точке равновесия потребителя (точке Хикса)
во вспомогательной точке равновесия потребителя (точке Хикса) 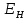 .
.Следовательно, вспомогательная бюджетная линия (линия Хикса) должна иметь тот же угол наклона, что и бюджетная линия
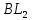 (описывающаяся уравнением
(описывающаяся уравнением 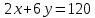 ), но являться касательной к первоначальной кривой безразличия потребителя
), но являться касательной к первоначальной кривой безразличия потребителя 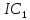 .
.Тогда система уравнений, из решения которой можно определить вспомогательный товарный набор
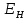 выглядит следующим образом:
выглядит следующим образом: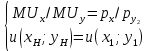 ;
;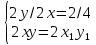 .
.Первое равенство преобразуется в:
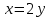 .
.Подставляем полученное выражение и известные значения
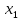 и
и 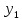 во второе выражение:
во второе выражение: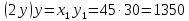 ;
;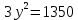 ;
;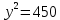 ;
;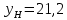 ед.
ед.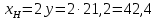
ед.
Следовательно, эффект замены
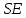 по Хиксу составляет:
по Хиксу составляет: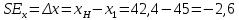 ;
;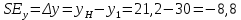 .
.Эффект дохода
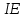 по Хиксу равен:
по Хиксу равен: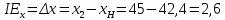 ;
;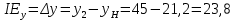 .
.Общий эффект
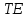 , рассчитанный по изменениям количеств товаров
, рассчитанный по изменениям количеств товаров  и
и  :
: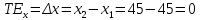 ;
;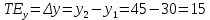 .
.Проверяем, определяя общий эффект
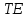 , как сумму эффектов дохода и замещения:
, как сумму эффектов дохода и замещения: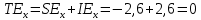 ;
;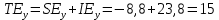 .
.Вывод: поскольку снижение цены товара
 вызвало повышенный спрос, то данный товар является нормальным (товаром высокого качества).
вызвало повышенный спрос, то данный товар является нормальным (товаром высокого качества).Практическое задание 4
Тема 3. Поведение производителя и конкуренция
Задачи
Технологическая норма замещения факторов
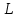 и
и 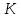 равна
равна 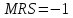 . Предположим, что фирма готова произвести тот же самый объем выпуска, но сократить использование фактора
. Предположим, что фирма готова произвести тот же самый объем выпуска, но сократить использование фактора 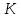 на
на 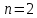 единицы. Сколько дополнительных единиц фактора
единицы. Сколько дополнительных единиц фактора 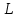 потребуется фирме?
потребуется фирме?Решение
Формула расчета технологической нормы замещения факторов
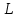 и
и 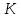
имеет вид:
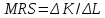 ,
,где
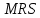 – технологическая норма замещения факторов
– технологическая норма замещения факторов  и
и  ;
;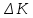 – изменение количества применяемого в производственном процессе фактора
– изменение количества применяемого в производственном процессе фактора  ;
; 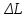 – изменение количества применяемого в производственном процессе фактора
– изменение количества применяемого в производственном процессе фактора  .
.Выражаем из этой формулы изменение количества фактора
 :
: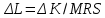 ;
;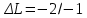 ;
;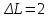 единицы фактора
единицы фактора  .
.Графическое решение представлено на рисунке.

Рис. Изменение количества фактора
 при сокращении использования фактора
при сокращении использования фактора 
Из рисунка следует, что если фирма желает остаться на прежней изокванте (линии равного выпуска)
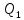 , то при сокращении использования фактора
, то при сокращении использования фактора  (смещении из точки
(смещении из точки 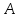 в точку
в точку 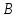 ) она должна вовлечь в производство дополнительное количество фактора
) она должна вовлечь в производство дополнительное количество фактора  .
.Вывод: расчеты показывают, что количество использования фактора
 необходимо увеличить на 2 единицы.
необходимо увеличить на 2 единицы.Практическое задание 5
Тема 4. Рыночные структуры и стратегия поведения
Задачи
1. Предположим, что на рынке действуют две фирмы, функции общих издержек
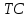 заданы уравнениями:
заданы уравнениями: 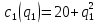 и
и 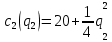 . Рыночный спрос описывается функцией:
. Рыночный спрос описывается функцией: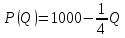 ,
,где
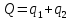 .
. Определите объем продаж, который будет у каждой фирмы, и цену, которая установится на рынке, если:
- фирмы конкурируют по Курно;
- фирмы конкурируют по Бертрану;
- фирмы конкурируют по сценарию Штакельберга.
Изобразите решение на графике.
Решение
В модели некооперированной дуополии Курно каждый дуополист исходит из предположения, что его соперник не изменит своего выпуска в ответ на его собственное решение. Это значит, что, принимая его, дуополист руководствуется стремлением к максимизации своей прибыли, полагая выпуск другого дуополиста заданным.
В данной модели состояние устойчивого равновесия в отрасли достигается в точке пересечения кривых реагирования дуополистов – точке равновесия Курно-Нэша. Кривые реагирования (кривые наилучшего ответа) – это множества точек наивысшей прибыли, которую может получить один из дуополистов при данной величине выпуска другого.
Представим функцию рыночного спроса в виде:
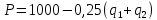 .
.Выразим функции прибыли каждого из дуополистов:
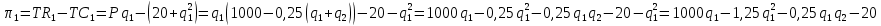 ;
;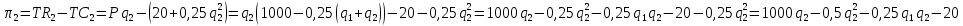 .
.Определим максимум полученных функций, найдя их первую производную и приравняв ее к 0:
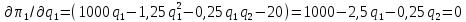 ;
;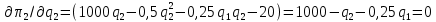 .
.Запишем уравнения кривых реагирования каждого из дуополистов, представив выпуск одного через выпуск другого.
Кривая реагирования дуополиста 1
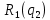 имеет вид:
имеет вид: