Файл: Задача Скорость прямолинейного движения SS(tt)S(t).docx
Добавлен: 25.10.2023
Просмотров: 101
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
(x) непрерывны на отрезке [a;b], дифференцируемы в окрестностях точки x0 (кроме может быть т. x0), в этой окрестности 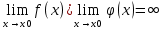 ,
, 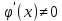 .
.
Если существует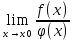 , то
, то 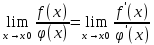 .
.
17. Раскрытие неопределённости различных видов (0*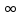 ,
, 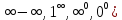
1. Пусть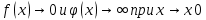 , то
, то
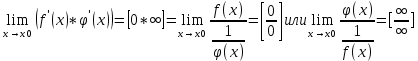 ,
,
2. Пусть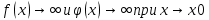 , тогда
, тогда
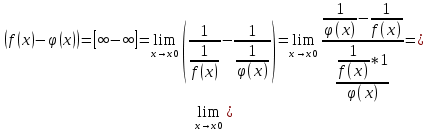
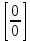
3. Пусть или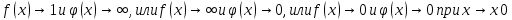 , тогда
, тогда 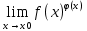 (сначала удобно логарифмировать)
(сначала удобно логарифмировать)
18. Возрастание и убывание функции. Экстремум ф-и. Наибольшее и наименьшее значение ф-и на отрезке.
Теорема 1 (необходимое условие).
Если дифференцируемая на интервале (a;b) ф-я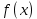 возрастает, то
возрастает, то 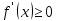 , а если убывает, то
, а если убывает, то 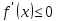 (для любых Х принадлежащих (a;b)).
(для любых Х принадлежащих (a;b)).
Теорема 2 (достаточное условие)
Если ф-я f(x) дифференцируема на интервале (a;b) и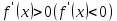 для любого хϵ(a; b), то эти ф-я возрастает (убывает) на интервале (a;b).
для любого хϵ(a; b), то эти ф-я возрастает (убывает) на интервале (a;b).
Экстремум функции
Значения функции в точке max (min) называются максимум (минимум) функции. Это и есть экстремумы функции.
Теорема 3 (необходимое условие экстремума)
Если дифференцируемая ф-я y= f(x) имеет экстремум в т. х0, то её производная равна в этой точке 0.
Непрерывная функция может иметь экстремум лишь в точках, где производная ф-и равна 0 или не существует. Такие точки называются критическими.
Теорема 4 (достаточное условие экстремума)
Если непрерывная ф-я y= f(x) дифференцируема в некоторой δ-окрестности критической т. х0 и при переходе через неё (слева направо) производная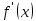 меняет знак с + на –, то х0 есть точка max, а если с – на +, то точка min.
меняет знак с + на –, то х0 есть точка max, а если с – на +, то точка min.
Правила исследования ф-и на экстремумы.
Теорема: Если в т. х0 первая производная ф-и f(x) равна 0 (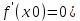 , а вторая существует и отлична от 0 (
, а вторая существует и отлична от 0 (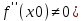 , то при
, то при 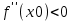 в т. х0 имеет максимум, а при
в т. х0 имеет максимум, а при 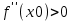 - минимум.
- минимум.
Наибольшее и наименьшее значение ф-и на отрезке
Пусть ф-я y= f(x) непрерывна на отрезке [a;b].
19. Выпуклость графика ф-и. Точки перегиба.
Выпуклость графика в т. Перегиба
Теорема: Если ф-я y=f(x) во всех точках (a;b) имеет отрицательную вторую производную, то график в этом интервале выпуклый вверх, если положительную – то график выпуклый вниз.
Теорема (достаточное условие сущ-я точек перегиба): Если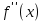 при переходе через т. х0, в которой она равна 0 или не существует, меняет знак, то точка графика с абсциссой х0 – точка перегиба.
при переходе через т. х0, в которой она равна 0 или не существует, меняет знак, то точка графика с абсциссой х0 – точка перегиба.
20. Асимптоты графика ф-и. Общая схема исследования ф-и и построения её графика.
Асимптотой кривой называется прямая, расстояние до которой от точки, лежащей на кривой, стремится к 0 при неограниченном удалении от начала координат этой точки по кривой.
Прямая х=а является вертикальной асимптотой графика ф-и y=f(x), если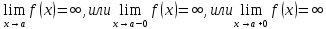
Уравнение наклонной асимптоты будем искать в виде y=kx+b, где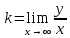 ,
, 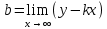 , следовательно если k=0, то
, следовательно если k=0, то 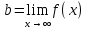 , поэтому y=b – ур-е горизонтальной асимтоты.
, поэтому y=b – ур-е горизонтальной асимтоты.
Схема исследования ф-и
21. Понятие неопределенного интеграла. Его свойства.
Функция F(x) называется первообразной ф-и f(x) на (a;b), если при любом xϵ(a;b) выполняется равенство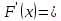 f(x) (или d F(x)= f(x)dx).
f(x) (или d F(x)= f(x)dx).
Теорема: Если F(x) является первообразной ф-и f(x) на (a;b), то множество всех первообразных для f(x) задаётся функцией F(x)+С.
Множество всех первообразных ф-й F(x)+С для f(x) наз-ся неопределённым интегралом от ф-и F(x) и обозначается: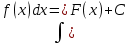 , где f(x) – подынтегральная функция,
, где f(x) – подынтегральная функция, 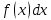 – подынтегральное выражение, x – переменная интегрирования.
– подынтегральное выражение, x – переменная интегрирования.
 Геометрически неопр. интеграл представляет собой семейство «параллельных» кривых y=F(x)+C. График каждой первообразной наз-ся интегральной кривой.
Геометрически неопр. интеграл представляет собой семейство «параллельных» кривых y=F(x)+C. График каждой первообразной наз-ся интегральной кривой.
Свойства:
22. Метод непосредственного интегрирования
Это метод, при котором данный интеграл путём тождественных преобразований и применения свойств неопределённого интеграла приводится к одному или нескольким табличным интегралам.
Операция «Подведение под знак дифференциала»: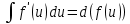
23. Метод интегрирования подстановкой (замены переменной)
Формула: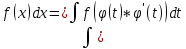 . После решения необходимо вернуться к начальной переменной.
. После решения необходимо вернуться к начальной переменной.
24. Метод интегрирования по частям
Пусть u=u(x) и v=v(x), тогда d(u*v)=u*dv+v*du
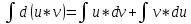 или
или 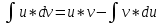
25. Понятие рациональной функции. Многочлен. Дробно-рациональная функция.
Функция вида Pn(x)=a0xn+a1xn-1+a2x2+…+an-1x+an, где nϵN, ai(i=0,1,…,n) – постоянные коэффициенты, называется многочленом или целой рациональной ф-ей, n – степень многочлена.
Теорема 1: Если х1 есть корень многочлена Pn(x), то многочлен делится без остатка на (x-x1):
Pn(x)=(х-х1)* Pn-1(x)
Теорема 2 (основная теорема алгебры): Всякий многочлен n-ой степени (n>0) имеет по крайней мере хотя бы один корень действительный или комплексный.
Теорема 3: Всякий многочлен Pn(x) можно представить в виде Pn(x)=a0(x-x1)(x-x2)…(x-xn)
Теорема 4: Если многочлен Pn(x) тождественно равен 0, то все его коэффициенты равны 0.
Теорема 5: Если два многочлена тождественно равны друг другу, то коэффициенты одного многочлена равны соответствующим коэф. другого.
Дробно-рациональная функция
Это функция, равная отношению двух многочленов f(x)=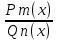
Рациональная дробь называется правильной, если m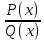 можно представить в виде суммы многочлена L(x)+
можно представить в виде суммы многочлена L(x)+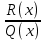 , где
, где 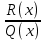 - правильная рац. дробь (
- правильная рац. дробь (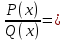 L(x)+
L(x)+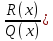 .
.
Правильные рациональные дроби вида:
(где A, a, M, N, p, q - действительные числа) - которые называются рациональными дробями I, II, III и IV типов
Т.
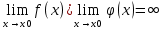 ,
, 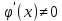 .
. Если существует
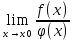 , то
, то 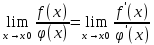 .
.17. Раскрытие неопределённости различных видов (0*
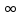 ,
, 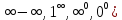
1. Пусть
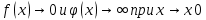 , то
, то 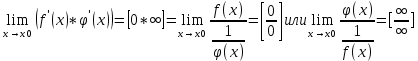 ,
,2. Пусть
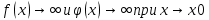 , тогда
, тогда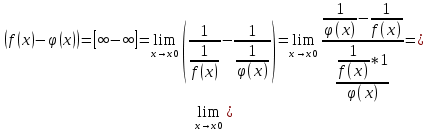
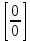
3. Пусть или
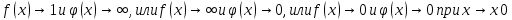 , тогда
, тогда 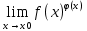 (сначала удобно логарифмировать)
(сначала удобно логарифмировать)18. Возрастание и убывание функции. Экстремум ф-и. Наибольшее и наименьшее значение ф-и на отрезке.
Теорема 1 (необходимое условие).
Если дифференцируемая на интервале (a;b) ф-я
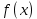 возрастает, то
возрастает, то 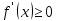 , а если убывает, то
, а если убывает, то 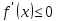 (для любых Х принадлежащих (a;b)).
(для любых Х принадлежащих (a;b)).Теорема 2 (достаточное условие)
Если ф-я f(x) дифференцируема на интервале (a;b) и
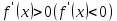 для любого хϵ(a; b), то эти ф-я возрастает (убывает) на интервале (a;b).
для любого хϵ(a; b), то эти ф-я возрастает (убывает) на интервале (a;b).Экстремум функции
Значения функции в точке max (min) называются максимум (минимум) функции. Это и есть экстремумы функции.
Теорема 3 (необходимое условие экстремума)
Если дифференцируемая ф-я y= f(x) имеет экстремум в т. х0, то её производная равна в этой точке 0.
Непрерывная функция может иметь экстремум лишь в точках, где производная ф-и равна 0 или не существует. Такие точки называются критическими.
Теорема 4 (достаточное условие экстремума)
Если непрерывная ф-я y= f(x) дифференцируема в некоторой δ-окрестности критической т. х0 и при переходе через неё (слева направо) производная
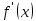 меняет знак с + на –, то х0 есть точка max, а если с – на +, то точка min.
меняет знак с + на –, то х0 есть точка max, а если с – на +, то точка min. Правила исследования ф-и на экстремумы.
-
Найти критические точки ф-и y= f(x) -
Выбрать те, которые являются внутренними точками области определения ф-ии -
Исследовать знак производной слева и справа от каждой из них -
Выписать точки экстремума (если есть) и вычислить значения ф-и в них
Теорема: Если в т. х0 первая производная ф-и f(x) равна 0 (
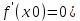 , а вторая существует и отлична от 0 (
, а вторая существует и отлична от 0 (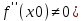 , то при
, то при 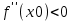 в т. х0 имеет максимум, а при
в т. х0 имеет максимум, а при 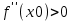 - минимум.
- минимум.Наибольшее и наименьшее значение ф-и на отрезке
Пусть ф-я y= f(x) непрерывна на отрезке [a;b].
-
Найти критические точки на интервале (a;b) -
Вычислить значения ф-и в них -
Вычислить значения ф-и на концах отрезка -
Среди вычисленных значений выбрать наибольшее и наименьшее.
19. Выпуклость графика ф-и. Точки перегиба.
Выпуклость графика в т. Перегиба
-
График дифференцируемой ф-и y=f(x) наз-ся выпуклым вниз на (a;b) если он расположен выше любой её касательной на этом интервале. -
График дифференцируемой ф-и y=f(x) наз-ся выпуклым вверх на (a;b) если он расположен ниже любой её касательной на этом -
Точка графика непрерывной ф-и y=f(x), отделяющая его части разной выпуклости наз-ся точкой перегиба.
Теорема: Если ф-я y=f(x) во всех точках (a;b) имеет отрицательную вторую производную, то график в этом интервале выпуклый вверх, если положительную – то график выпуклый вниз.
Теорема (достаточное условие сущ-я точек перегиба): Если
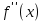 при переходе через т. х0, в которой она равна 0 или не существует, меняет знак, то точка графика с абсциссой х0 – точка перегиба.
при переходе через т. х0, в которой она равна 0 или не существует, меняет знак, то точка графика с абсциссой х0 – точка перегиба.20. Асимптоты графика ф-и. Общая схема исследования ф-и и построения её графика.
Асимптотой кривой называется прямая, расстояние до которой от точки, лежащей на кривой, стремится к 0 при неограниченном удалении от начала координат этой точки по кривой.
Прямая х=а является вертикальной асимптотой графика ф-и y=f(x), если
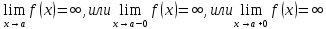
Уравнение наклонной асимптоты будем искать в виде y=kx+b, где
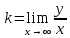 ,
, 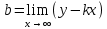 , следовательно если k=0, то
, следовательно если k=0, то 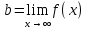 , поэтому y=b – ур-е горизонтальной асимтоты.
, поэтому y=b – ур-е горизонтальной асимтоты.Схема исследования ф-и
-
Найти обл опред ф-ии -
Найти (если возможно) точки пересечения графика с осями координат -
Найти интервалы знакопостоянства функции (промежутки, на к-х f(x)>0 или f(x)<0) -
Выяснить, является ли ф-я чётной (f(-x)=f(x)), нечётной (f(-x)=-f(x)) или общего вида -
Найти асимптоты графика ф-и -
Найти интервалы монотонности ф-и -
Найти экстремумы ф-и -
Найти интервалы выпуклости и точки перегиба графика ф-и
21. Понятие неопределенного интеграла. Его свойства.
Функция F(x) называется первообразной ф-и f(x) на (a;b), если при любом xϵ(a;b) выполняется равенство
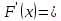 f(x) (или d F(x)= f(x)dx).
f(x) (или d F(x)= f(x)dx).Теорема: Если F(x) является первообразной ф-и f(x) на (a;b), то множество всех первообразных для f(x) задаётся функцией F(x)+С.
Множество всех первообразных ф-й F(x)+С для f(x) наз-ся неопределённым интегралом от ф-и F(x) и обозначается:
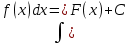 , где f(x) – подынтегральная функция,
, где f(x) – подынтегральная функция, 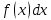 – подынтегральное выражение, x – переменная интегрирования.
– подынтегральное выражение, x – переменная интегрирования. Геометрически неопр. интеграл представляет собой семейство «параллельных» кривых y=F(x)+C. График каждой первообразной наз-ся интегральной кривой.
Геометрически неопр. интеграл представляет собой семейство «параллельных» кривых y=F(x)+C. График каждой первообразной наз-ся интегральной кривой.Свойства:
-
d(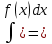 f(x)dx,
f(x)dx, 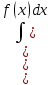
-
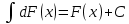
-
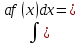 a
a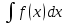 , a≠0
, a≠0 -
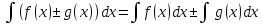
-
Инвариантность формулы интегрирования: если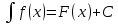 , то
, то 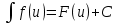 , где u=
, где u=
22. Метод непосредственного интегрирования
Это метод, при котором данный интеграл путём тождественных преобразований и применения свойств неопределённого интеграла приводится к одному или нескольким табличным интегралам.
Операция «Подведение под знак дифференциала»:
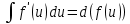
| | | | |
| | | | |
| | | | |
23. Метод интегрирования подстановкой (замены переменной)
Формула:
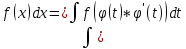 . После решения необходимо вернуться к начальной переменной.
. После решения необходимо вернуться к начальной переменной.24. Метод интегрирования по частям
Пусть u=u(x) и v=v(x), тогда d(u*v)=u*dv+v*du
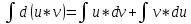 или
или 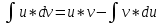
25. Понятие рациональной функции. Многочлен. Дробно-рациональная функция.
Функция вида Pn(x)=a0xn+a1xn-1+a2x2+…+an-1x+an, где nϵN, ai(i=0,1,…,n) – постоянные коэффициенты, называется многочленом или целой рациональной ф-ей, n – степень многочлена.
Теорема 1: Если х1 есть корень многочлена Pn(x), то многочлен делится без остатка на (x-x1):
Pn(x)=(х-х1)* Pn-1(x)
Теорема 2 (основная теорема алгебры): Всякий многочлен n-ой степени (n>0) имеет по крайней мере хотя бы один корень действительный или комплексный.
Теорема 3: Всякий многочлен Pn(x) можно представить в виде Pn(x)=a0(x-x1)(x-x2)…(x-xn)
Теорема 4: Если многочлен Pn(x) тождественно равен 0, то все его коэффициенты равны 0.
Теорема 5: Если два многочлена тождественно равны друг другу, то коэффициенты одного многочлена равны соответствующим коэф. другого.
Дробно-рациональная функция
Это функция, равная отношению двух многочленов f(x)=
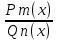
Рациональная дробь называется правильной, если m
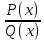 можно представить в виде суммы многочлена L(x)+
можно представить в виде суммы многочлена L(x)+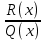 , где
, где 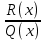 - правильная рац. дробь (
- правильная рац. дробь (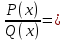 L(x)+
L(x)+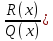 .
.Правильные рациональные дроби вида:
-
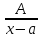
-
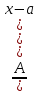 (k≥2, k ϵN)
(k≥2, k ϵN) -
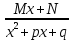
-
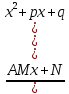 (k≥2)
(k≥2)
(где A, a, M, N, p, q - действительные числа) - которые называются рациональными дробями I, II, III и IV типов
Т.