Файл: 1. основные результаты и направления развития гидроаэромеханики буровых процессов.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 25.10.2023
Просмотров: 139
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
.
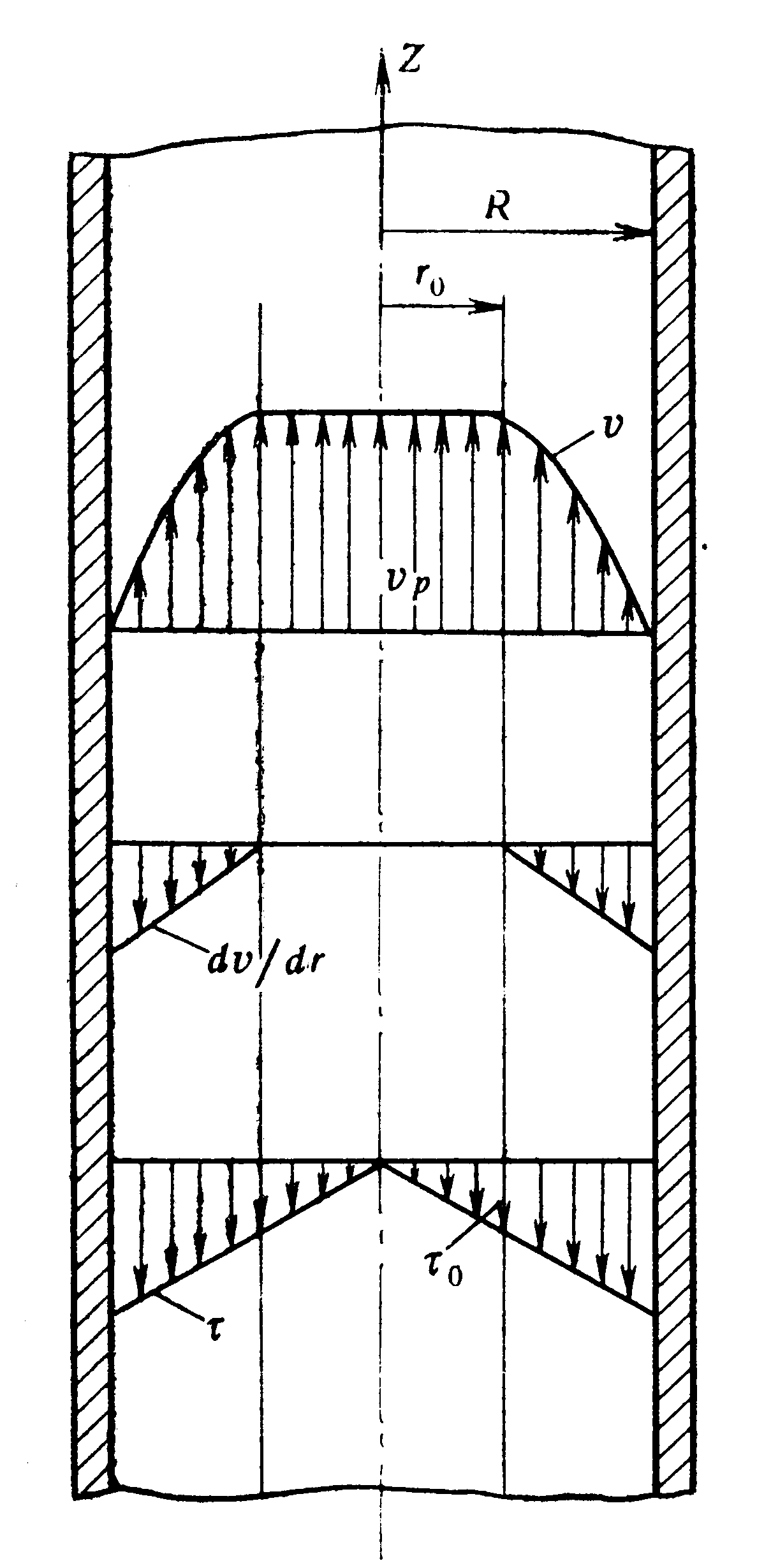
Рисунок. Распределение скоростей, напряжений и скоростей сдвига при ламинарном течении бингамовских жидкостей в круглой трубе.
В потоке есть зона течения (ядро), в которой жидкость перемещается как твердое тело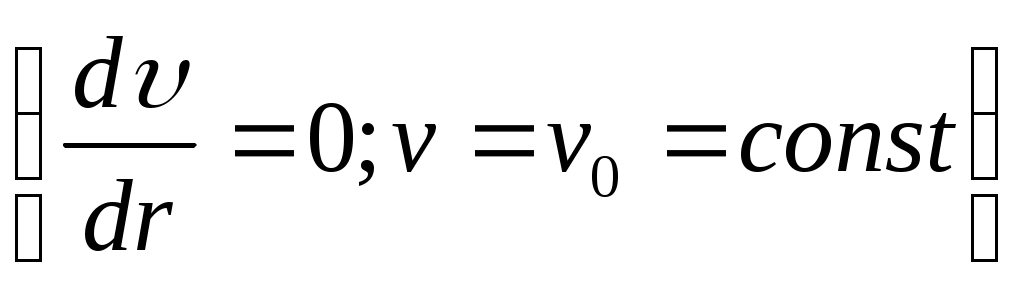 . Внутри ядра
. Внутри ядра 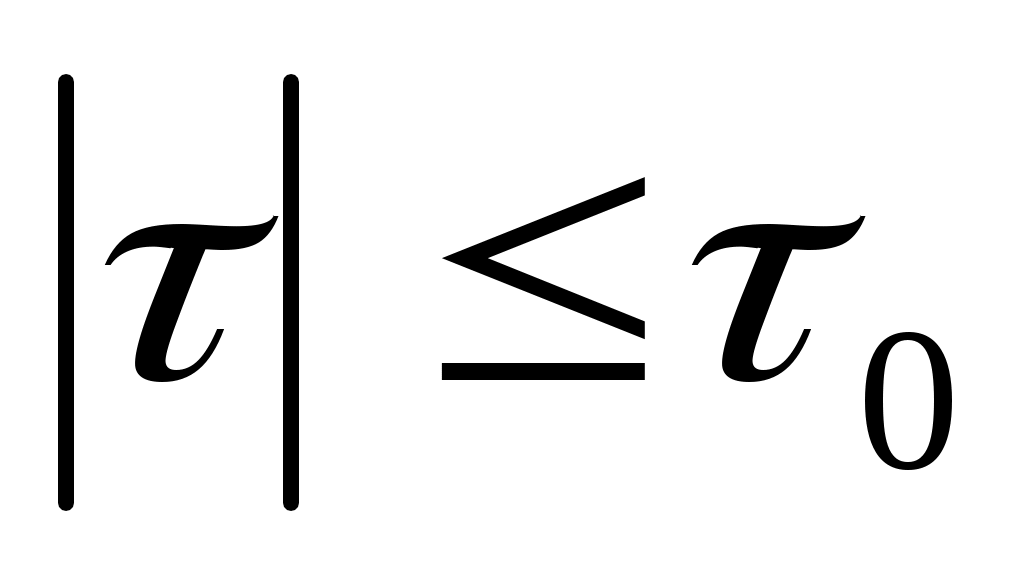 .
.
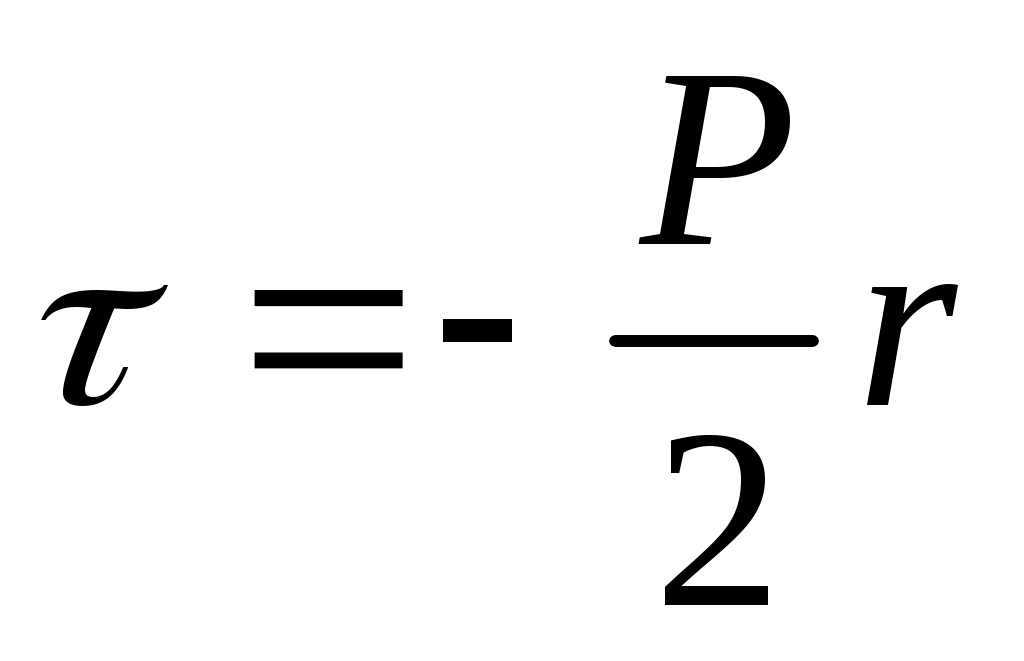 (2)
(2)
Напряжения отрицательны, т.е. действуют в направлении, обратном направлению течения. Обычно в расчетах знак не учитывают.
Для существования течения должно выполняться условие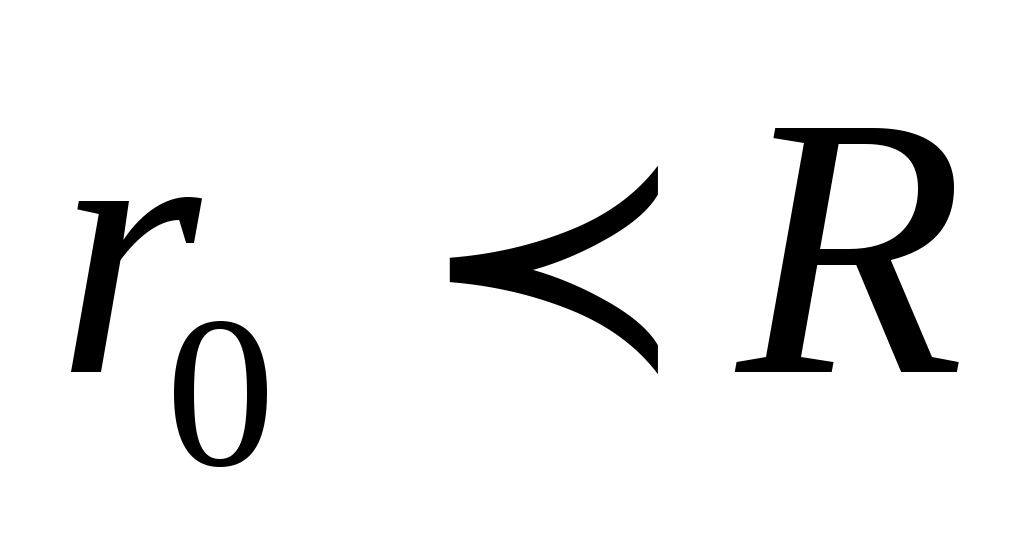 , т.е.
, т.е.
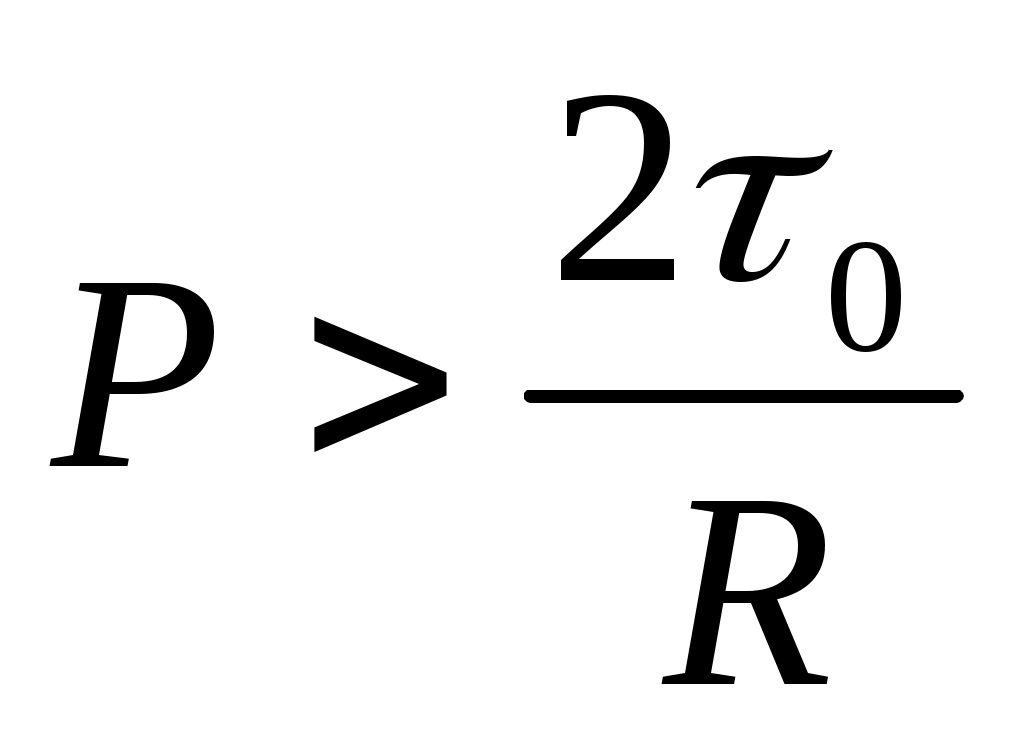 (3)
(3)
Из условия неразрывности скорости потока скорость движения ядра
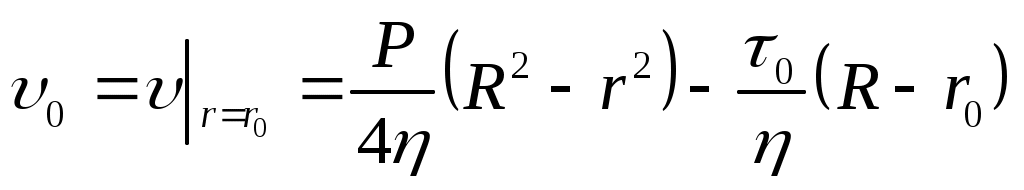 , (4)
, (4)
или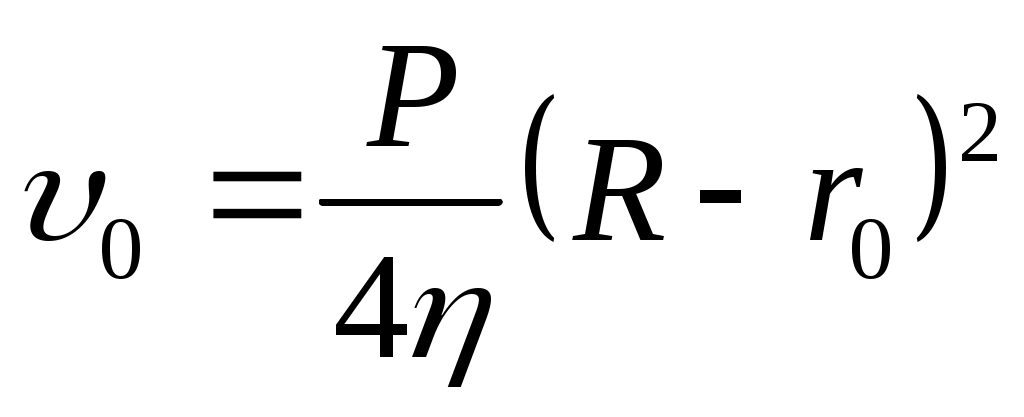
τс – напряжение сдвига на стенке канала.
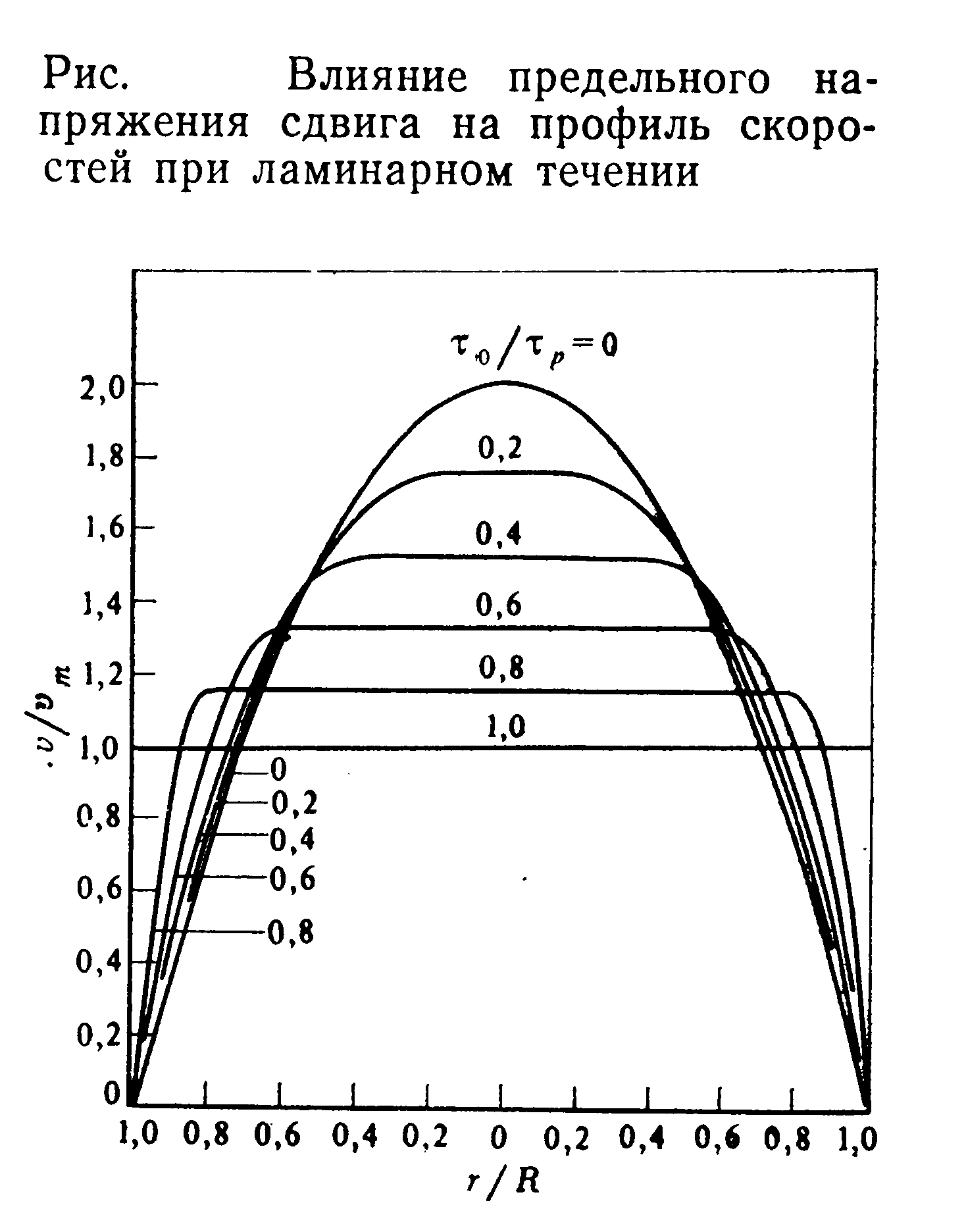
На рисунке наглядно показано влияние предельного напряжения сдвига на профиль скорости течения при определенном напряжении сдвига на стенке
на профиль скорости течения при определенном напряжении сдвига на стенке 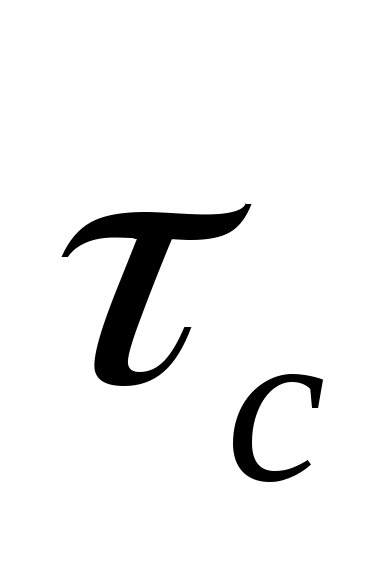 при ламинарном течении.
при ламинарном течении.
Объемный расход Q через трубу под действием градиента давления P
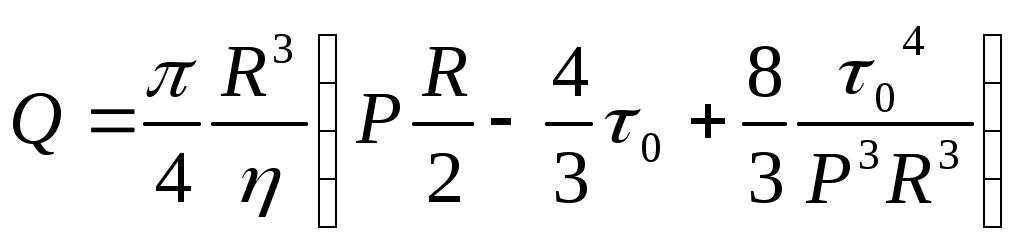 (5)
(5)
Если градиент давления, необходимый для начала течения, обозначить как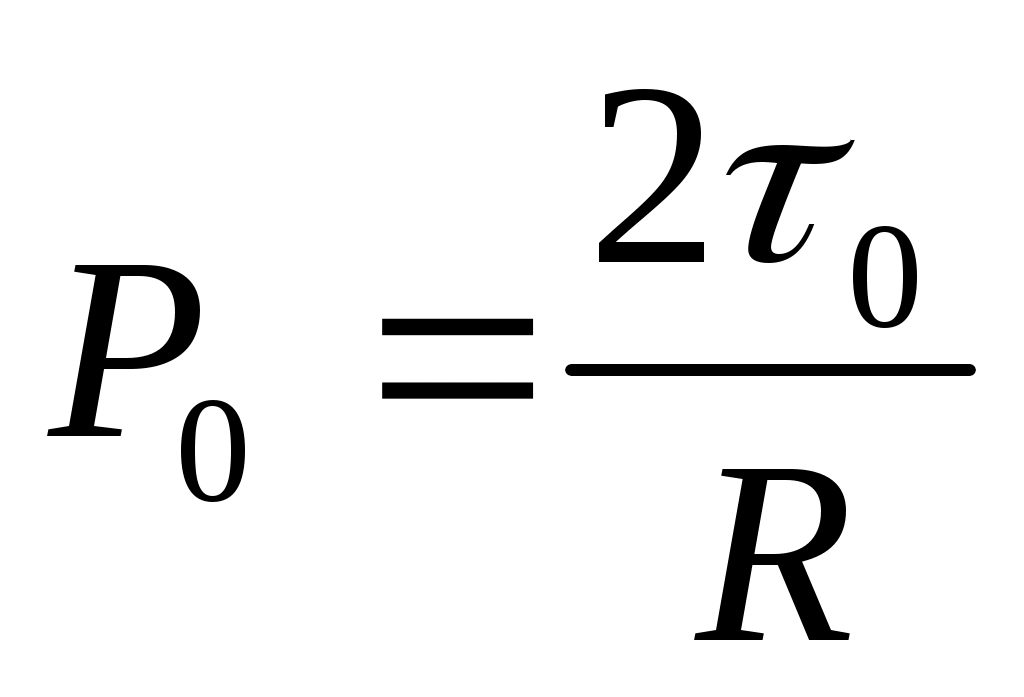 (6)
(6)
то (5) можно представить в виде
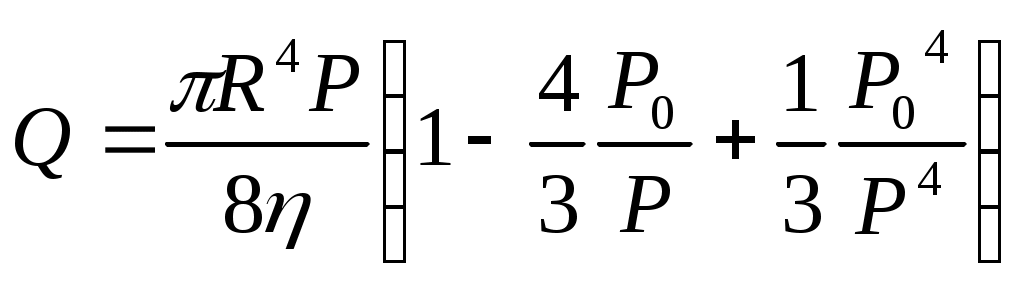 (7)
(7)
Формула (7) получена Букингамом в 1921г. Представляет собой обобщение уравнения Гагена-Пуазейля, которое применяется для ньютоновских жидкостей (τ0=0)
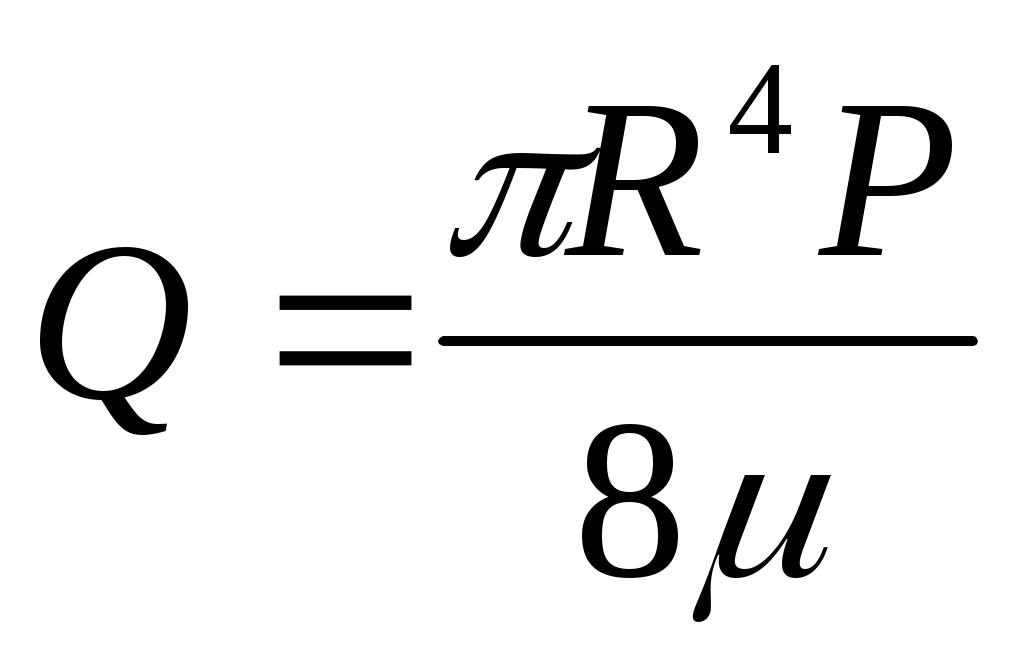 (8)
(8)
Напряжение сдвига на стенке трубы
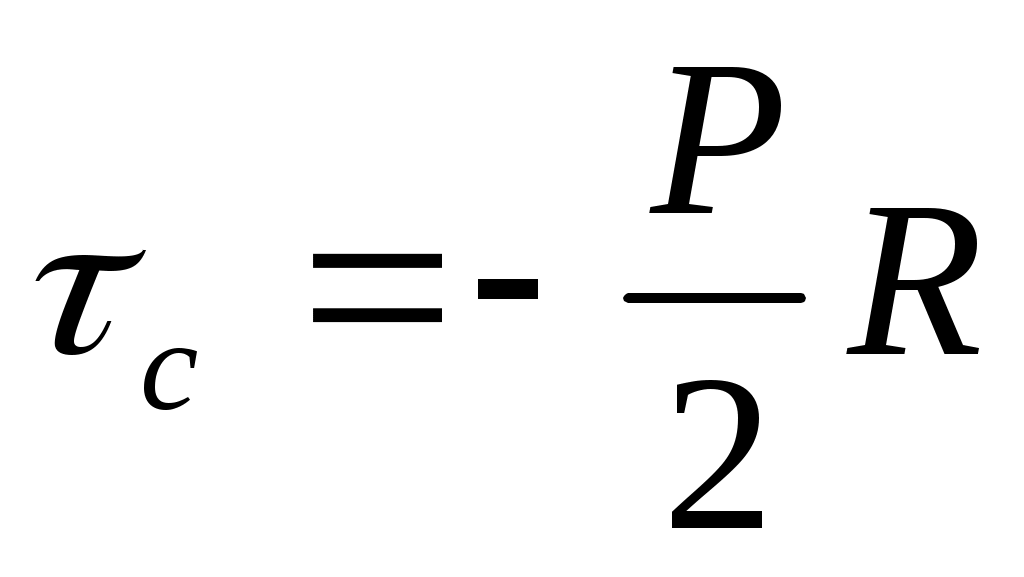 (9)
(9)
С учетом (9) выражение (7) можно записать по-другому (τс вводится по абсолютному значению)
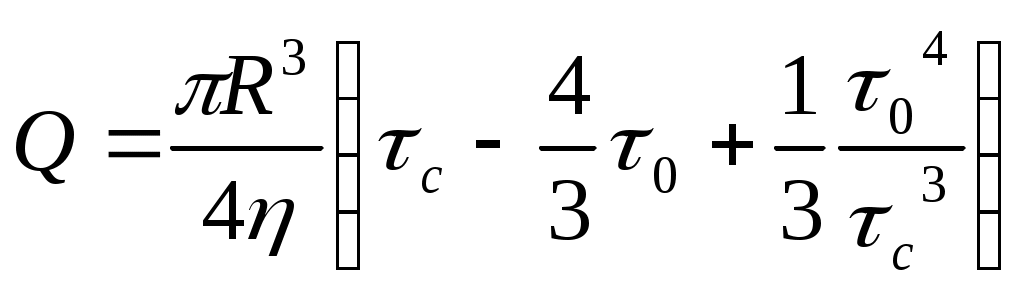 (10)
(10)
Если ввести среднюю скорость потока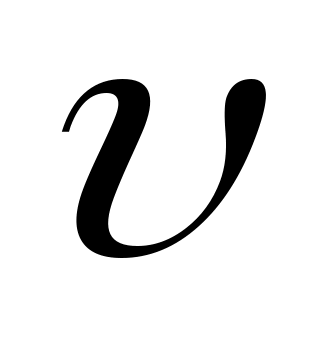
ср и диаметр трубы D, получим
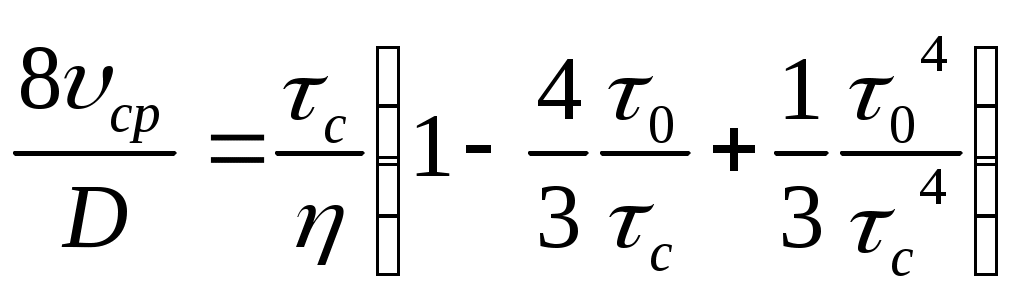 (11)
(11)
Величина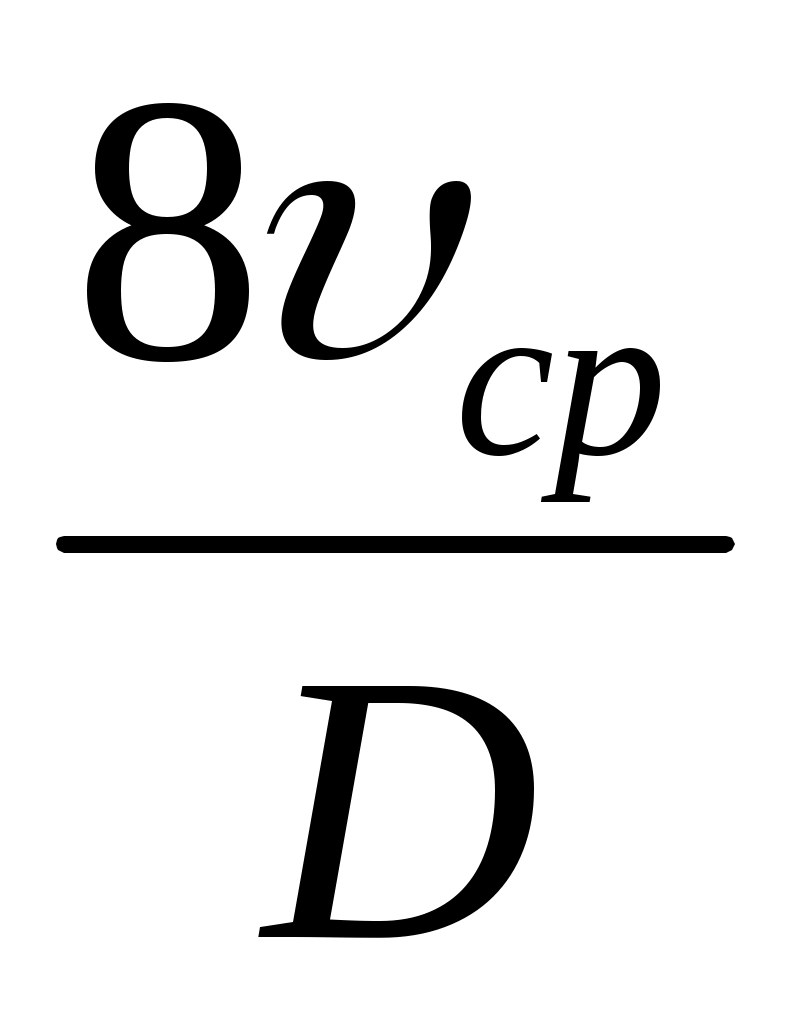 называется средней скоростью сдвига или кажущейся (номинальной) скоростью сдвига на стенке. Она равна скорости деформации жидкости вблизи стенки только для ньютоновских сред, когда величина в скобках (11) равна 1.
называется средней скоростью сдвига или кажущейся (номинальной) скоростью сдвига на стенке. Она равна скорости деформации жидкости вблизи стенки только для ньютоновских сред, когда величина в скобках (11) равна 1.
Сопоставляя (11) с (8), можно получить
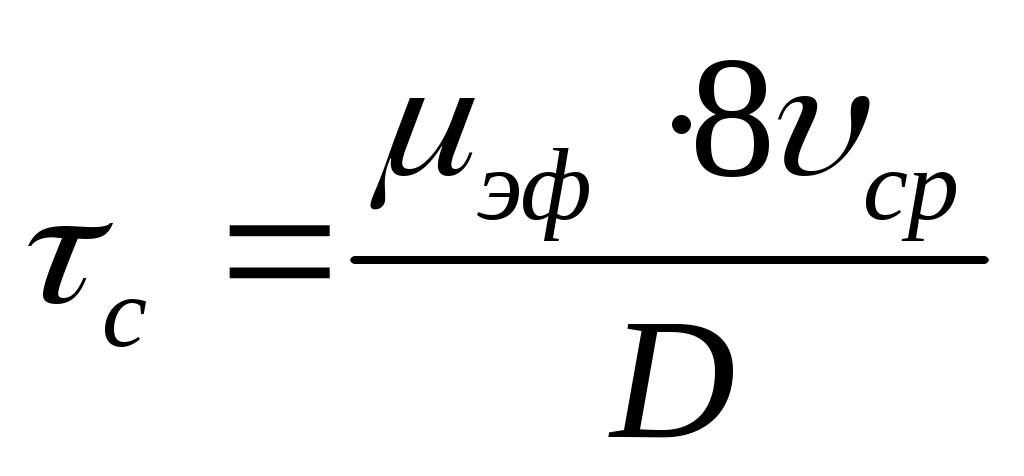 (12)
(12)
Для больших P Бингам предположил, что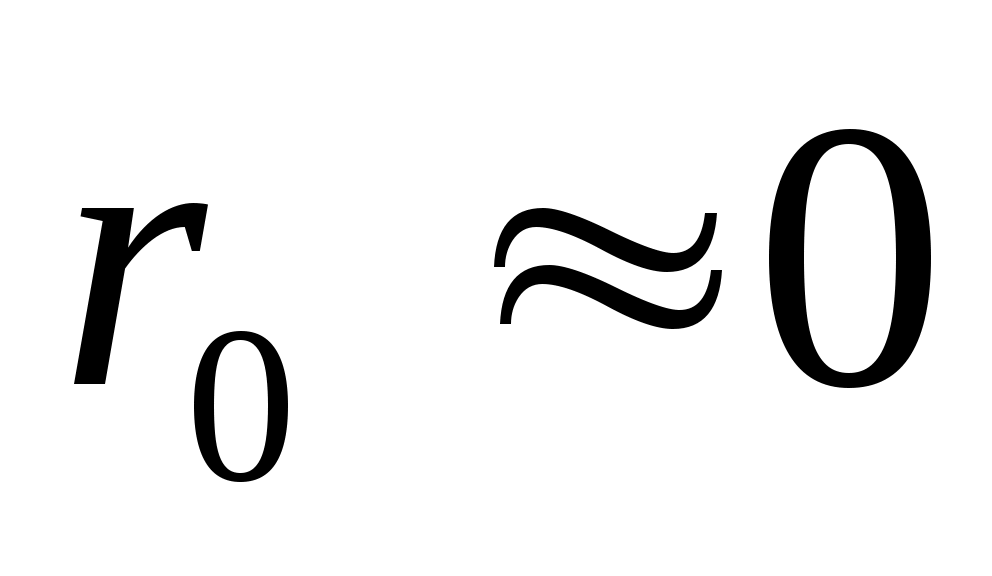 , имеет место вязкопластичное течение по всему сечению трубы, т.е. жесткое ядро отсутствует. Тогда
, имеет место вязкопластичное течение по всему сечению трубы, т.е. жесткое ядро отсутствует. Тогда
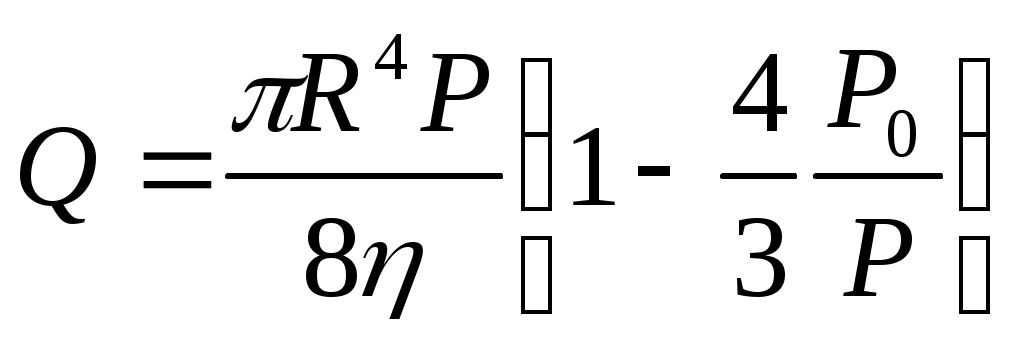 , (13)
, (13)
или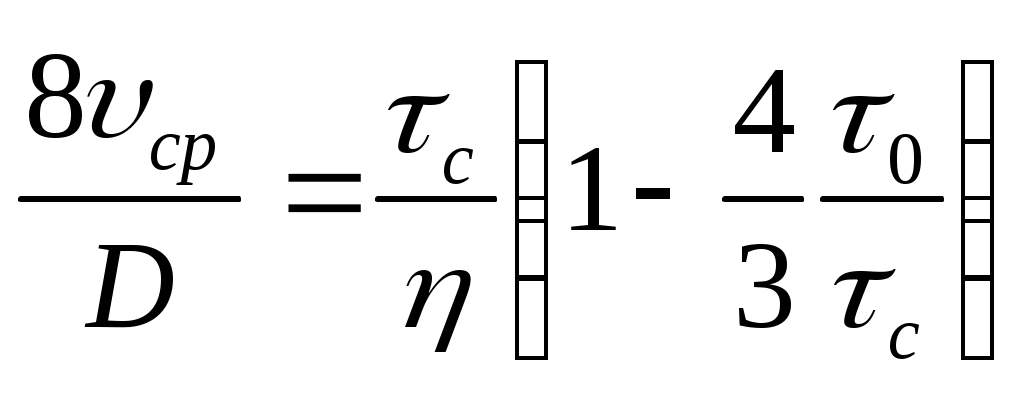 (14)
(14)
Выражение в скобках в уравнении (13) отличается от аналогичного в уравнении (7) лишь отсутствием последнего слагаемого, которым можно пренебречь, если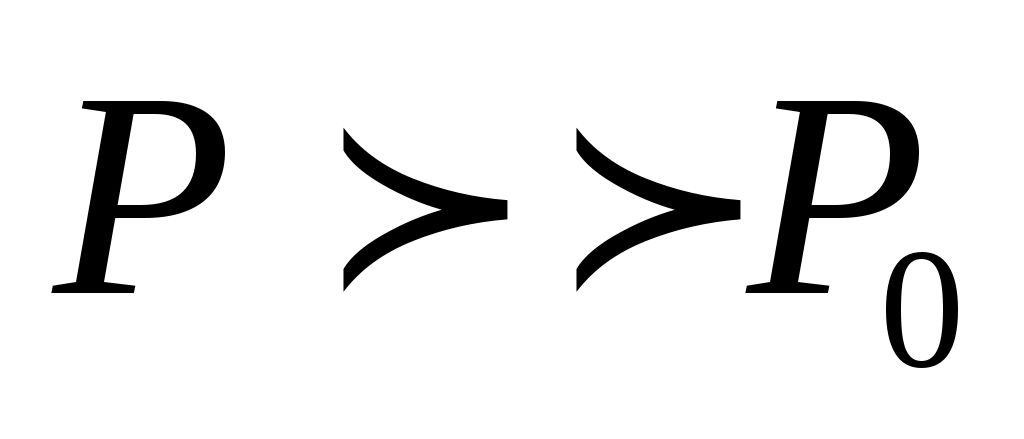 (или
(или 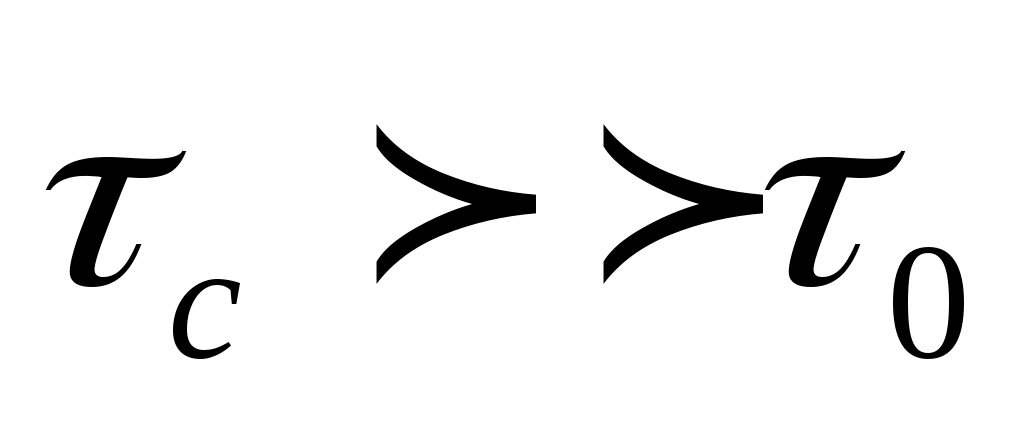 ).
).
В то же время, уравнения (12) и (14) позволяют определить эффективную вязкость бингамовских жидкостей
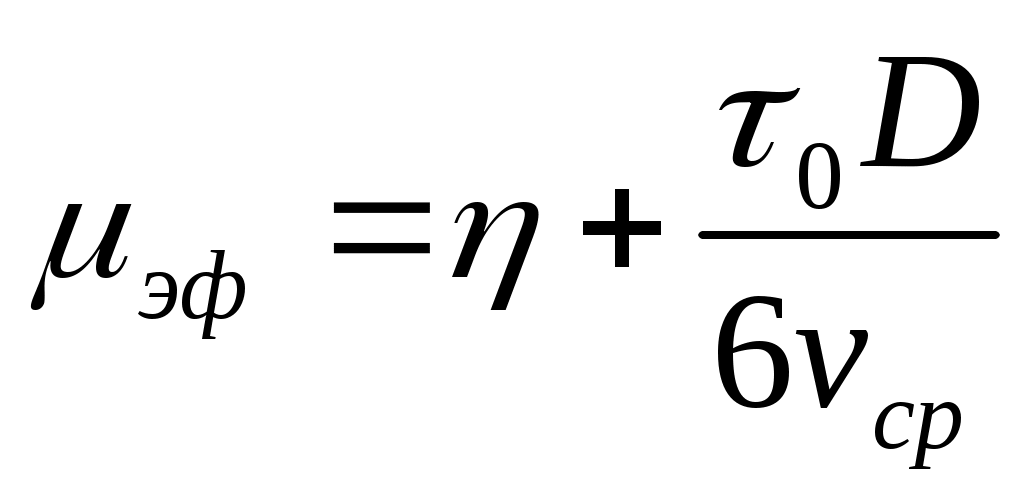 (15)
(15)
При бурении, как правило, требуется определять градиенты давления P (или полное давление P·l) по известному расходу Q. Однако, уравнение (7) трудно решать относительно P.
Было введено понятие коэффициента гидравлического сопротивления (безразмерный!)
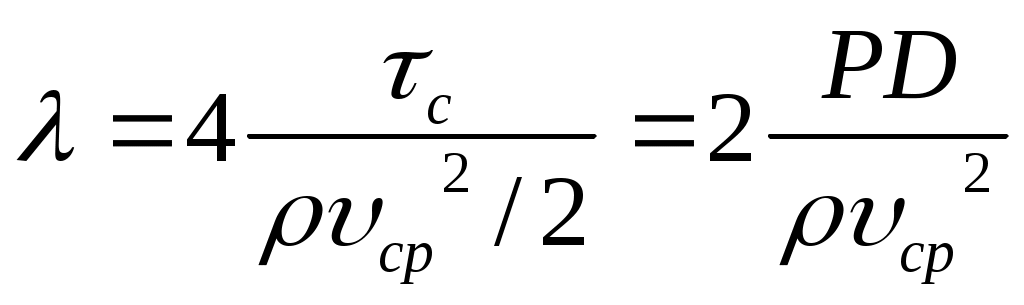 , (16)
, (16)
откуда
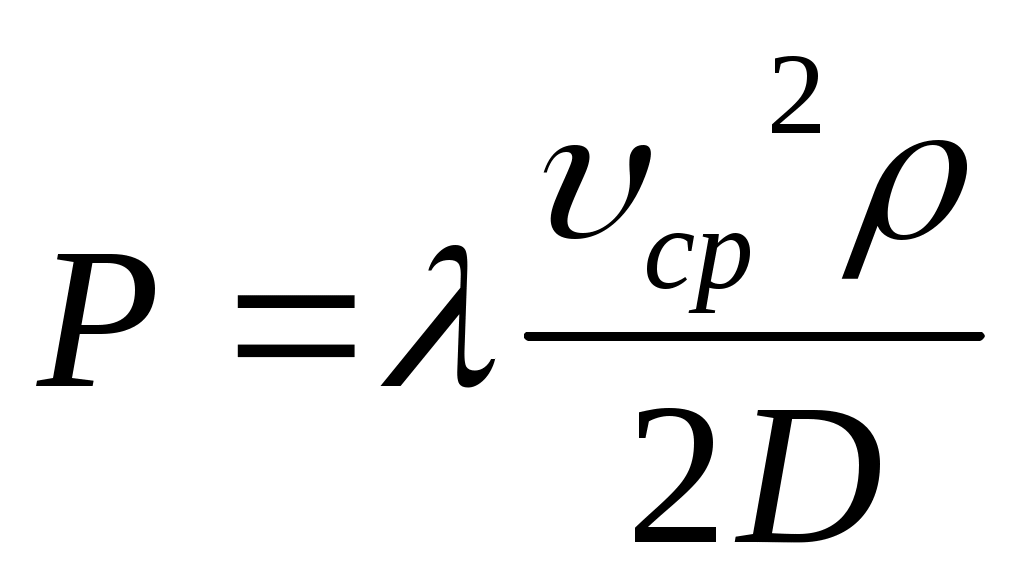 , Па/м (17)
, Па/м (17)
Эта зависимость называется формулой Дарси-Вейсбаха (домножив на l, получим давление в Па).
Безразмерный коэффициент λ есть учетверенное значение соотношения между напряжением сдвига на стенке и кинетической энергией потока, приходящейся на единицу объема.
Коэффициент λ является функцией безразмерных критериев:
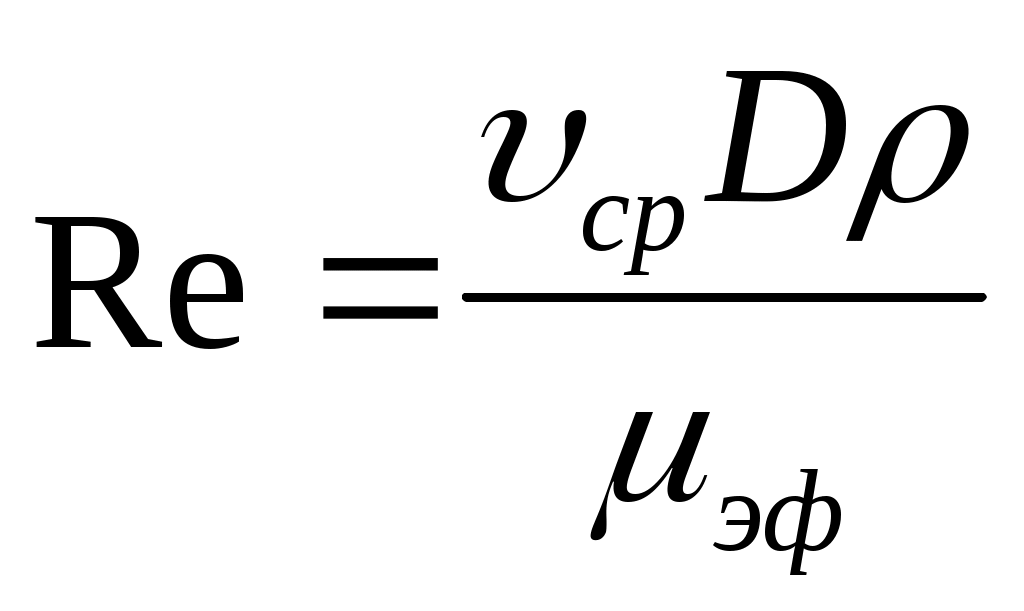
(18)
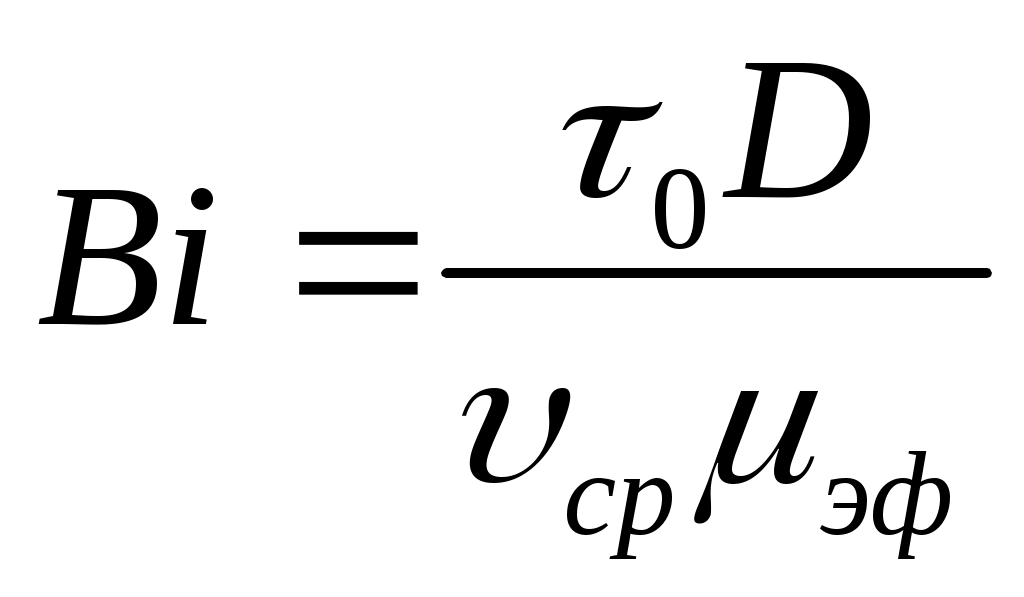 (19)
(19)
При использовании параметров Рейнольдса и Бингама
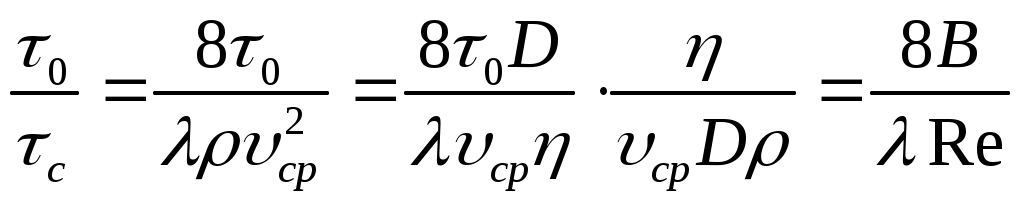 (20)
(20)
а также уравнения Букингама соотношение
 (21)
(21)
можно выразить только через безразмерные величины
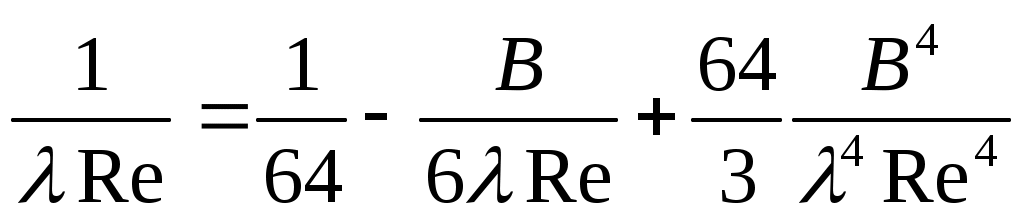 . (22)
. (22)
Это уравнение может быть представлено графически в виде зависимости от Re и В в качестве параметров.
от Re и В в качестве параметров.
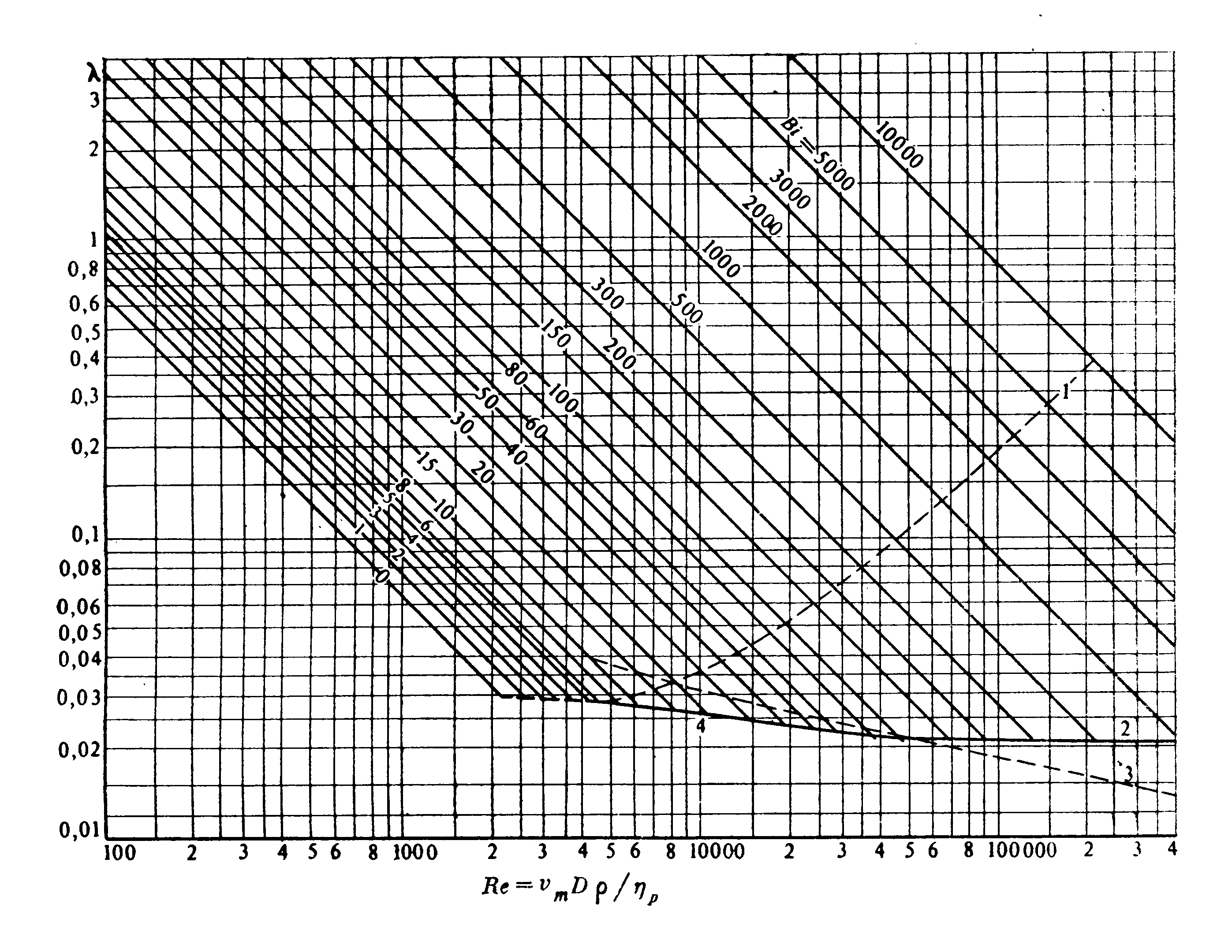
Часто используется и третья безразмерная комбинация параметров, предложенная Хедстремом:
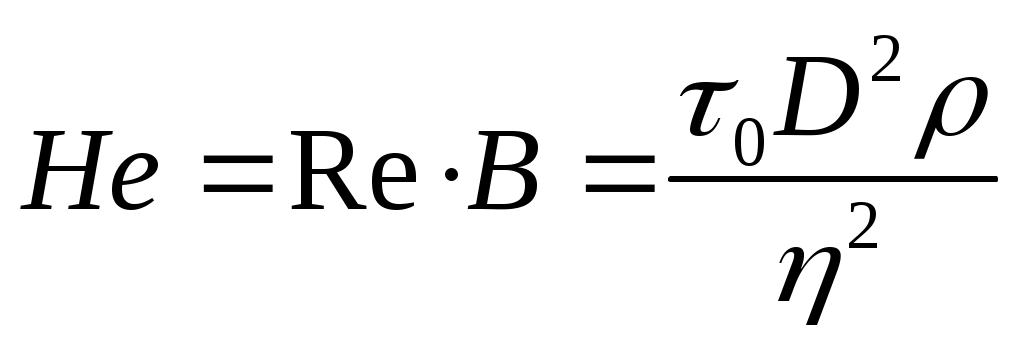 . (23)
. (23)
Уравнение (22) в этом случае принимает следующий вид:
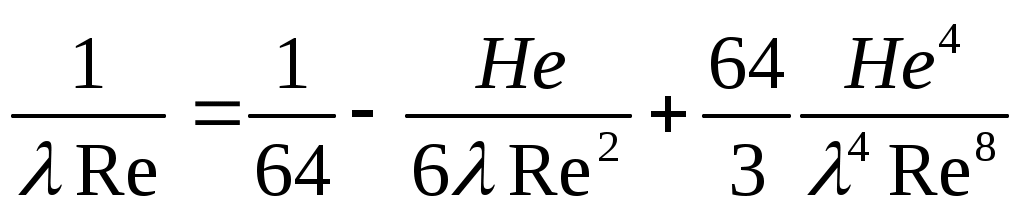 . (24)
. (24)
Для ньютоновских жидкостей В=Не=0, и уравнения сводятся к формуле Стокса
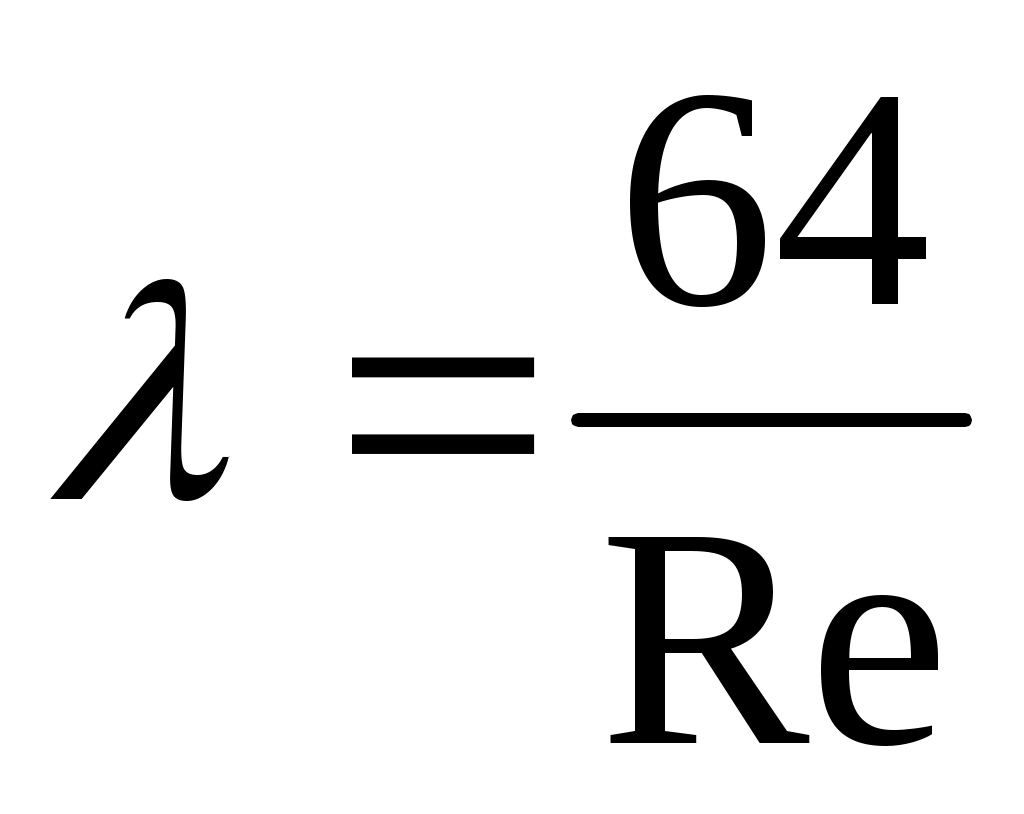 . (25)
. (25)
Строго говоря, для вязкопластичных жидкостей Бингама-Шведова используется понятие обобщенного параметра Рейнольдса, который определяется через эффективную вязкость среды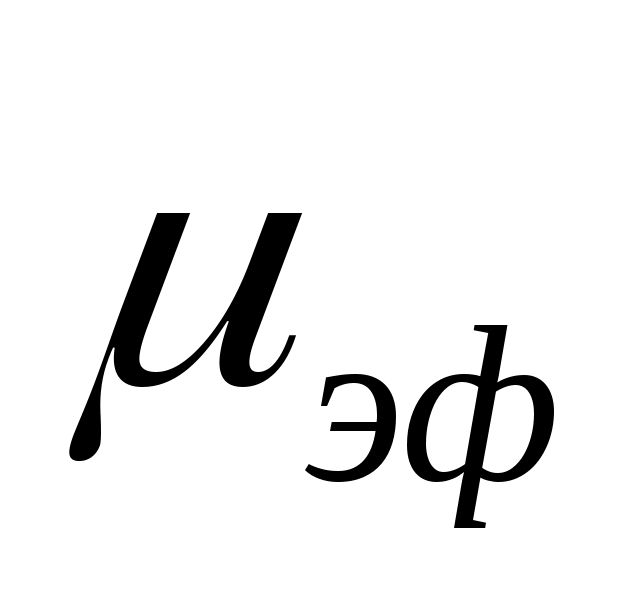 :
:
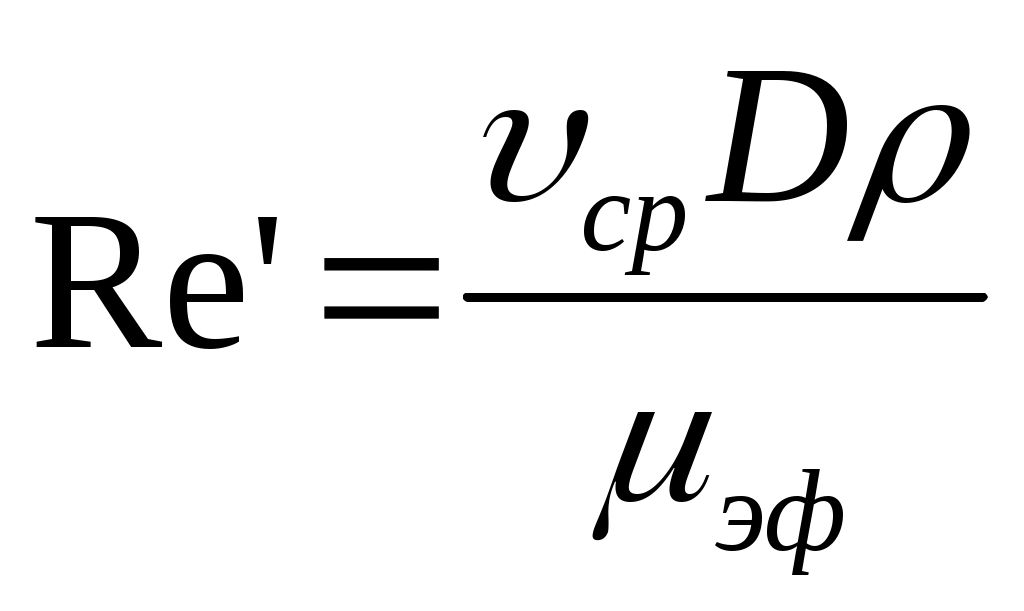 , (26)
, (26)
и, в первом приближении, допускается определять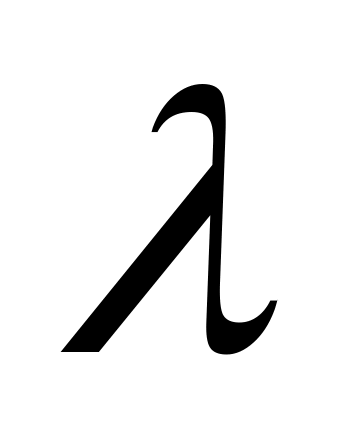 по формуле (25), заменив в ней Re на
по формуле (25), заменив в ней Re на 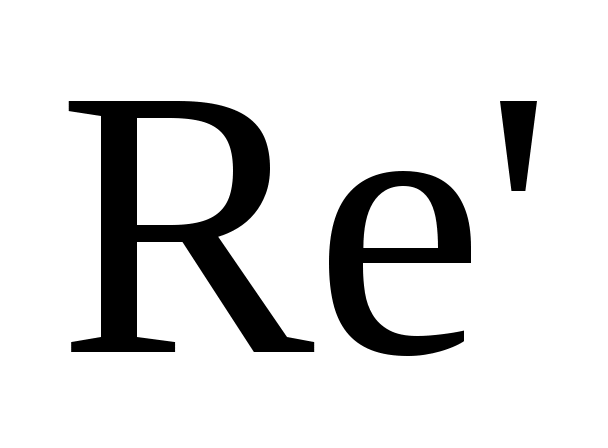 . При
. При 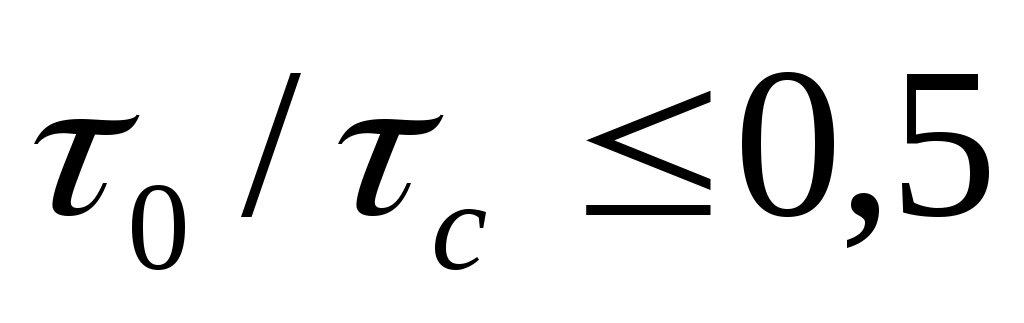 погрешность не превышает 6%.
погрешность не превышает 6%.
Структурное и ламинарное течение в кольцевых каналах.
1. Ньютоновские жидкости.
Общее уравнение движения
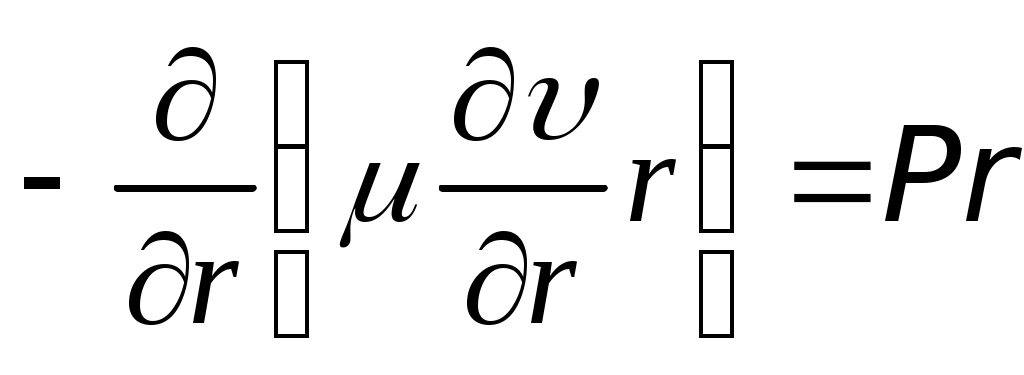 (27)
(27)
Двукратное интегрирование при граничных условиях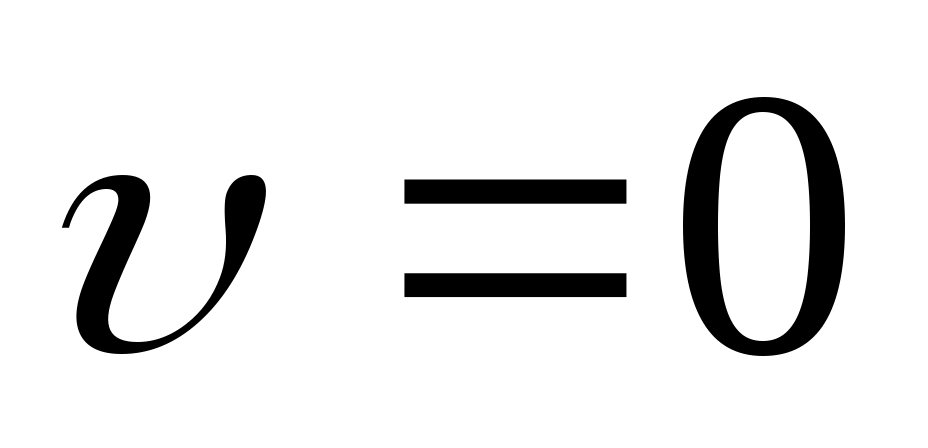 при
при 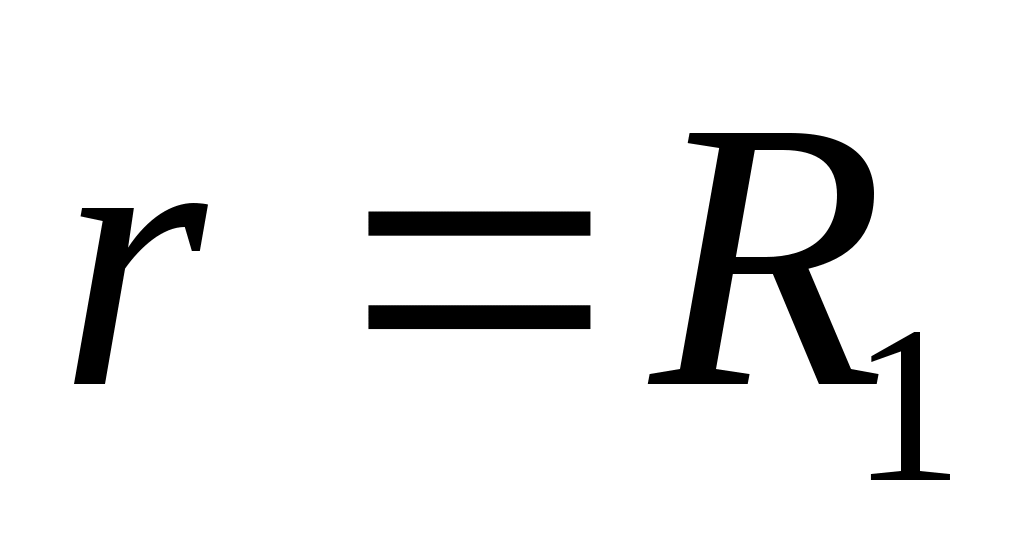 и
и 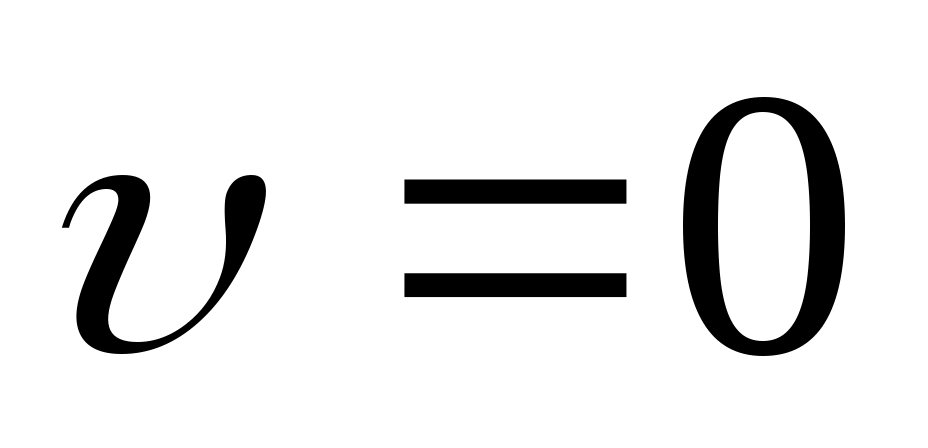
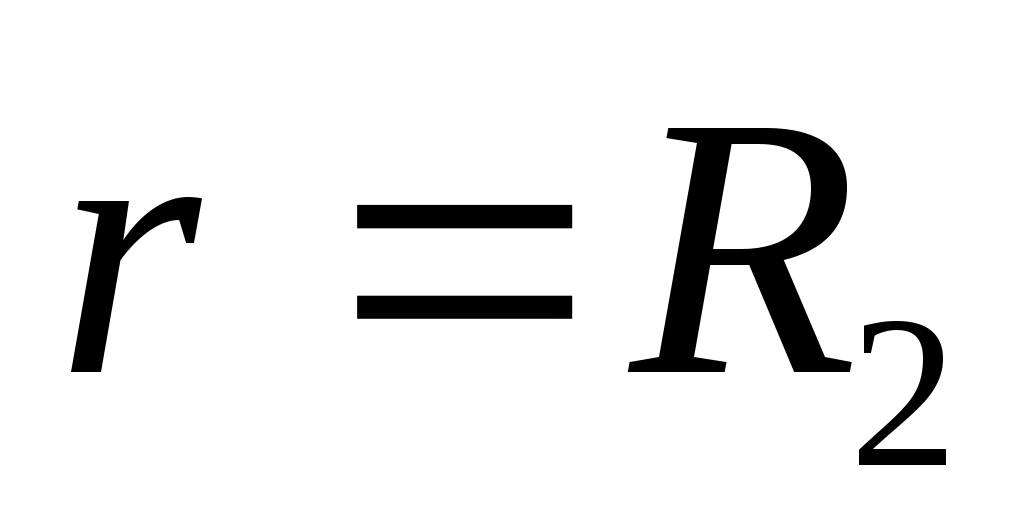 дает общее уравнение для распределения скорости потока в поперечном сечении кольцевого канала
дает общее уравнение для распределения скорости потока в поперечном сечении кольцевого канала
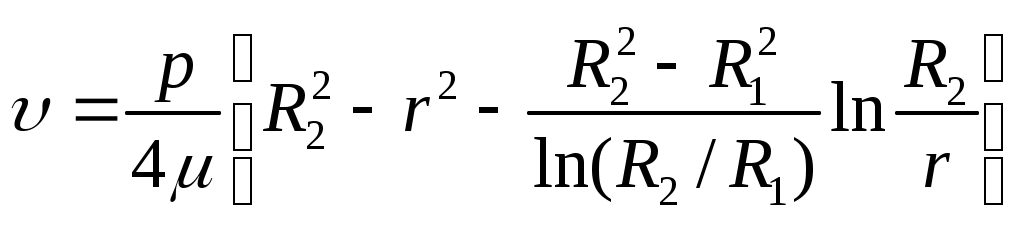 . (28)
. (28)
Объемный расход в кольцевом канале
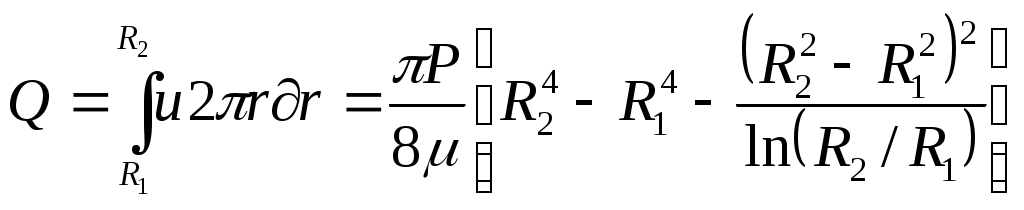 . (29)
. (29)
Формула (29) впервые была получена Ж. Буссинеском.
Зная , можно найти значение средней скорости
, можно найти значение средней скорости
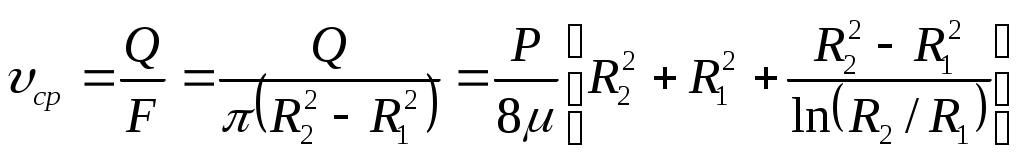 . (30)
. (30)
И далее, по формуле Дарси-Вейсбаха получим зависимость для коэффициента гидравлических сопротивлений :
:
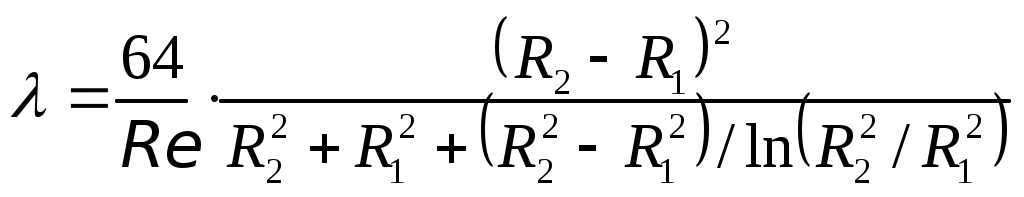 . (31)
. (31)
Параметр Рейнольдса для кольцевого канала
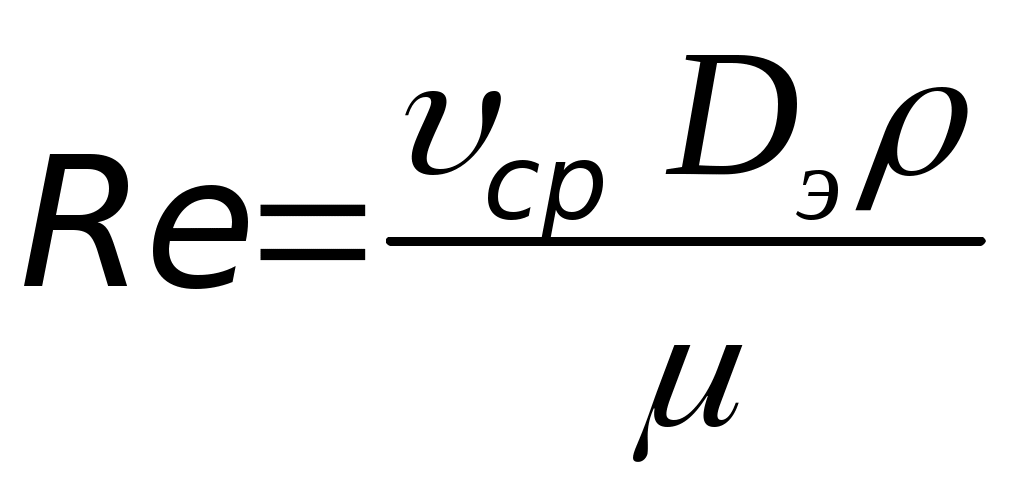 , (32)
, (32)
где Dэ – эквивалентный диаметр кольцевого канала.
Для канала с любой формой поперечного сечения эквивалентный диаметр
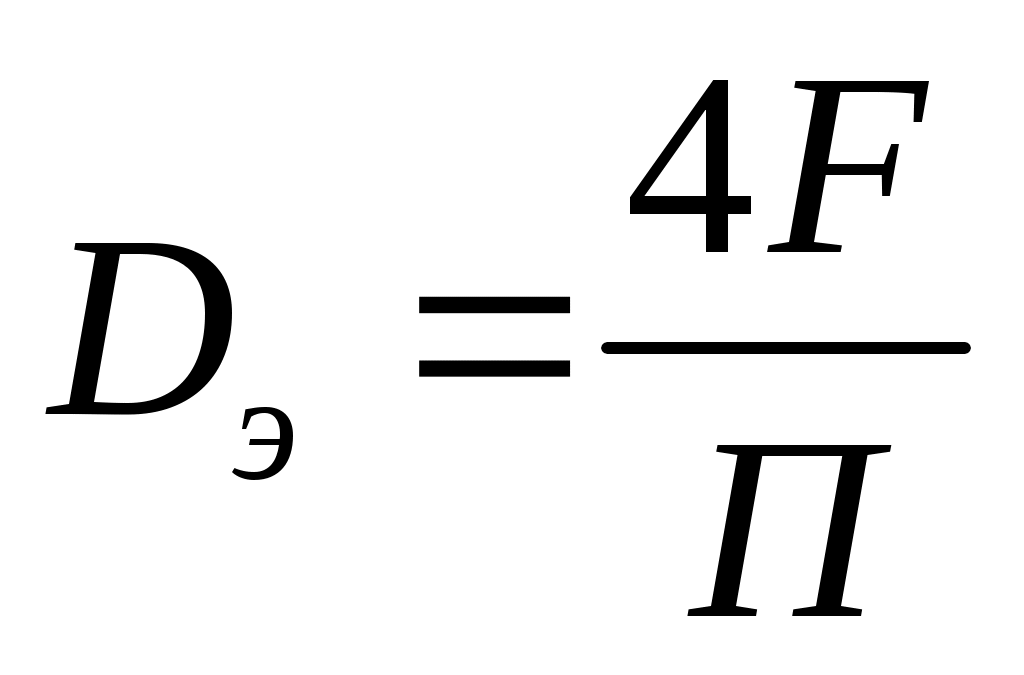 , (33)
, (33)
где F – площадь поперечного сечения канала; П – “смоченный” периметр.
Для кольцевого канала
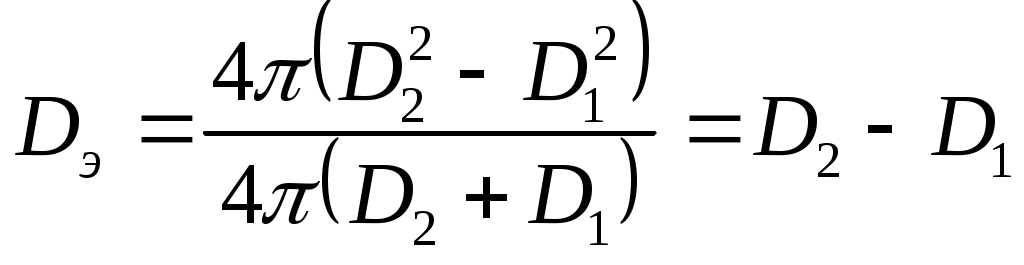 . (34)
. (34)
По данным экспериментальных исследований при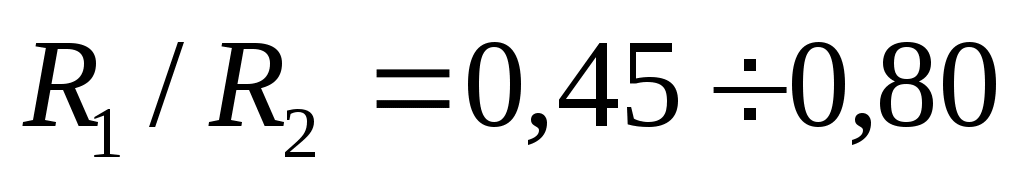 значение второго сомножителя в (31) изменяется от 1,485 до 1,495, т.е. с погрешностью 1% ее можно принять равной 1,5.
значение второго сомножителя в (31) изменяется от 1,485 до 1,495, т.е. с погрешностью 1% ее можно принять равной 1,5.
Тогда
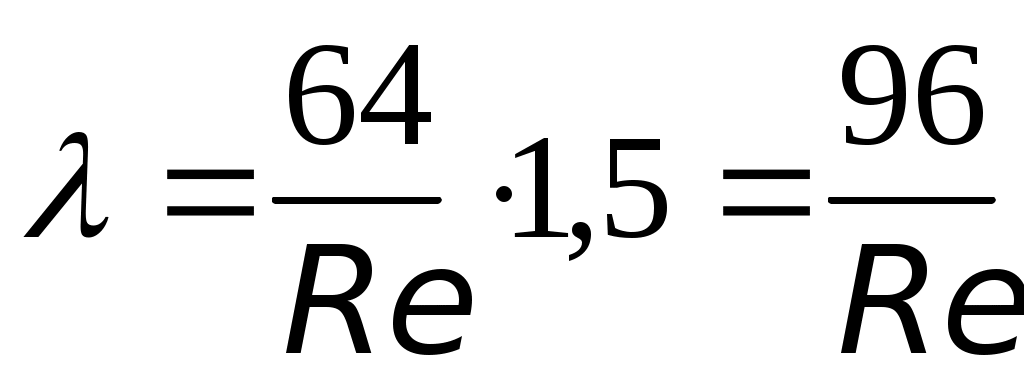 . (35)
. (35)
2. Жидкости Бингама-Шведова.
Вывод формул, связывающих градиент давления Р и объемный расход Q для вязкопластичных жидкостей, представляет собой весьма сложную задачу.

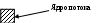
Рисунок. Распределение скоростей, напряжений и скоростей сдвига при ламинарном течении бингамовских жидкостей в круглой трубе.
В потоке есть зона течения (ядро), в которой жидкость перемещается как твердое тело
Распределение напряжений
Напряжения отрицательны, т.е. действуют в направлении, обратном направлению течения. Обычно в расчетах знак не учитывают.
Для существования течения должно выполняться условие
Из условия неразрывности скорости потока скорость движения ядра
или

τс – напряжение сдвига на стенке канала.
На рисунке наглядно показано влияние предельного напряжения сдвига
Объемный расход Q через трубу под действием градиента давления P
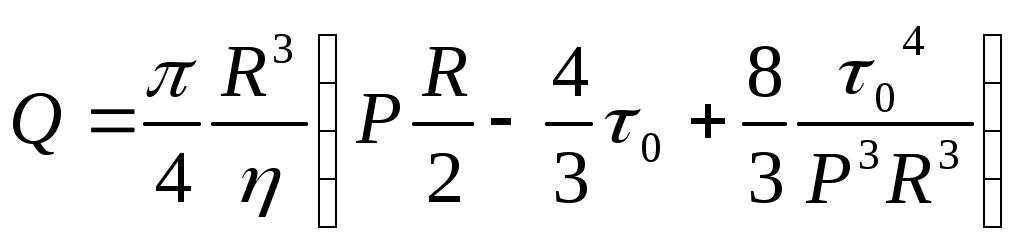 (5)
(5)Если градиент давления, необходимый для начала течения, обозначить как
то (5) можно представить в виде
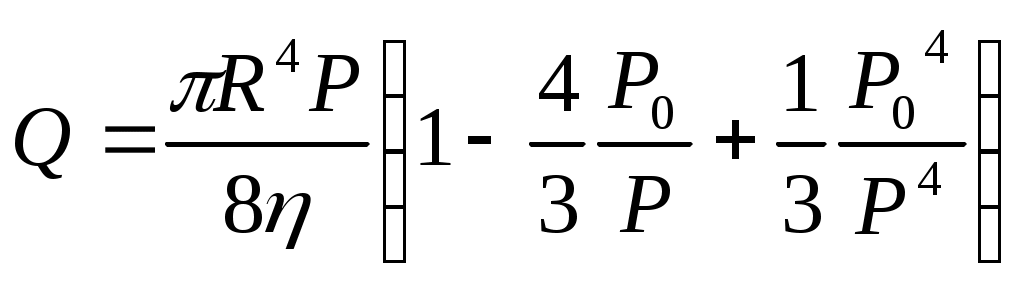 (7)
(7)Формула (7) получена Букингамом в 1921г. Представляет собой обобщение уравнения Гагена-Пуазейля, которое применяется для ньютоновских жидкостей (τ0=0)
Напряжение сдвига на стенке трубы
С учетом (9) выражение (7) можно записать по-другому (τс вводится по абсолютному значению)
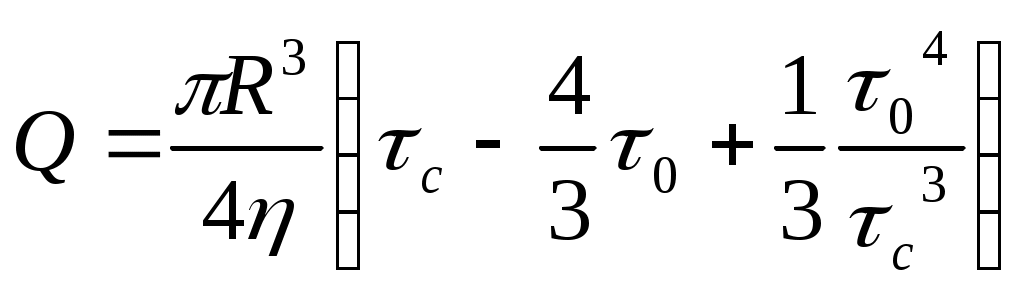 (10)
(10)Если ввести среднюю скорость потока
ср и диаметр трубы D, получим
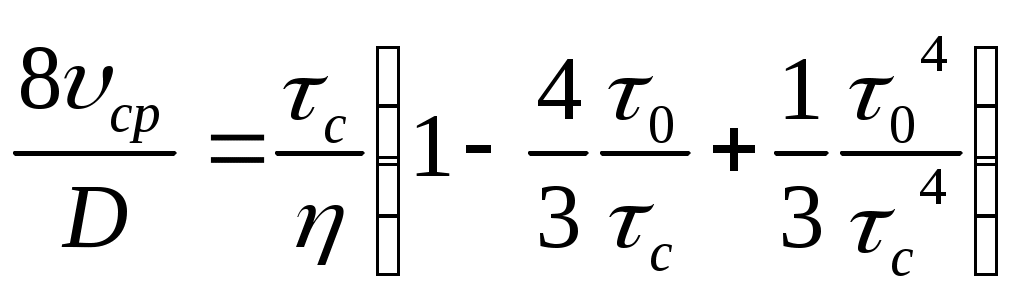 (11)
(11)Величина
Сопоставляя (11) с (8), можно получить
Для больших P Бингам предположил, что
или
Выражение в скобках в уравнении (13) отличается от аналогичного в уравнении (7) лишь отсутствием последнего слагаемого, которым можно пренебречь, если
В то же время, уравнения (12) и (14) позволяют определить эффективную вязкость бингамовских жидкостей
При бурении, как правило, требуется определять градиенты давления P (или полное давление P·l) по известному расходу Q. Однако, уравнение (7) трудно решать относительно P.
Было введено понятие коэффициента гидравлического сопротивления (безразмерный!)
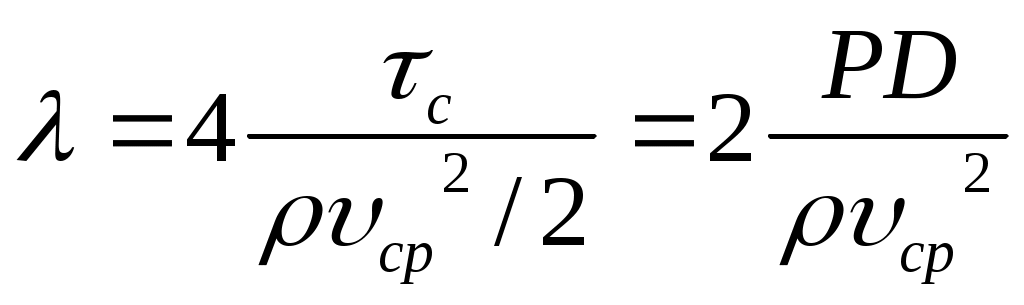 , (16)
, (16)откуда
Эта зависимость называется формулой Дарси-Вейсбаха (домножив на l, получим давление в Па).
Безразмерный коэффициент λ есть учетверенное значение соотношения между напряжением сдвига на стенке и кинетической энергией потока, приходящейся на единицу объема.
Коэффициент λ является функцией безразмерных критериев:
-
критерия Рейнольдса (для бингамовских жидкостей)
(18)
-
критерия Бингама (Сен-Венана) (критерий пластичности)
При использовании параметров Рейнольдса и Бингама
а также уравнения Букингама соотношение
 (21)
(21)можно выразить только через безразмерные величины
Это уравнение может быть представлено графически в виде зависимости

Часто используется и третья безразмерная комбинация параметров, предложенная Хедстремом:
Уравнение (22) в этом случае принимает следующий вид:
Для ньютоновских жидкостей В=Не=0, и уравнения сводятся к формуле Стокса
Строго говоря, для вязкопластичных жидкостей Бингама-Шведова используется понятие обобщенного параметра Рейнольдса, который определяется через эффективную вязкость среды
и, в первом приближении, допускается определять
Структурное и ламинарное течение в кольцевых каналах.
1. Ньютоновские жидкости.
Общее уравнение движения
Двукратное интегрирование при граничных условиях
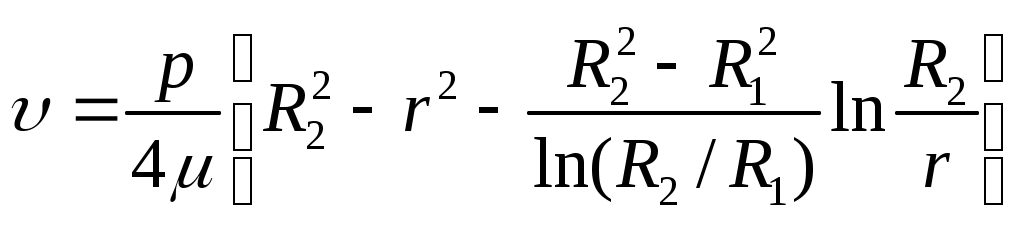 . (28)
. (28)Объемный расход в кольцевом канале
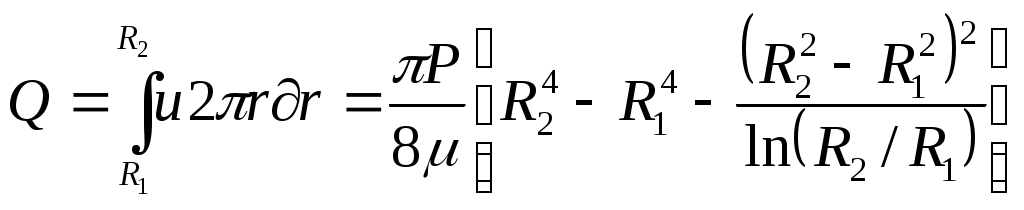 . (29)
. (29)Формула (29) впервые была получена Ж. Буссинеском.
Зная
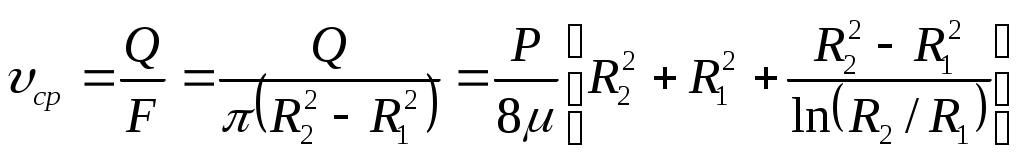 . (30)
. (30)И далее, по формуле Дарси-Вейсбаха получим зависимость для коэффициента гидравлических сопротивлений
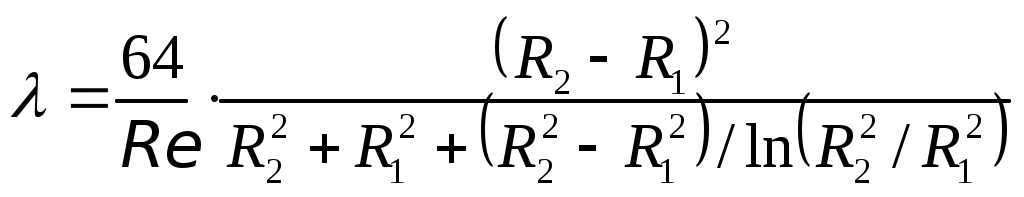 . (31)
. (31)Параметр Рейнольдса для кольцевого канала
где Dэ – эквивалентный диаметр кольцевого канала.
Для канала с любой формой поперечного сечения эквивалентный диаметр
где F – площадь поперечного сечения канала; П – “смоченный” периметр.
Для кольцевого канала
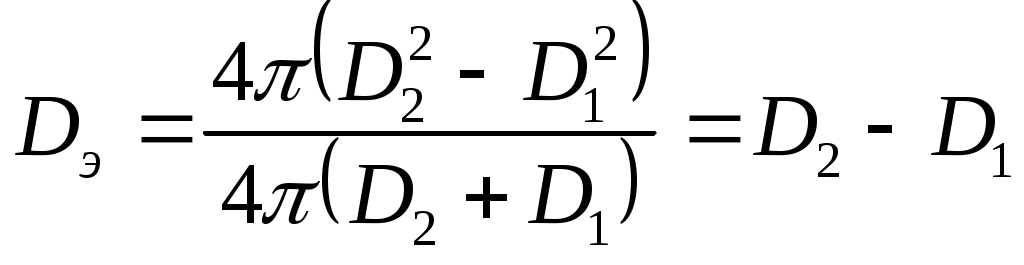 . (34)
. (34)По данным экспериментальных исследований при
Тогда
2. Жидкости Бингама-Шведова.
Вывод формул, связывающих градиент давления Р и объемный расход Q для вязкопластичных жидкостей, представляет собой весьма сложную задачу.