Файл: Сборник олимпиадных задач по математике для 5 класса.docx

Решение: Если бревно распилить на любое число частей , то частей всегда окажется больше, чем распилов. Если частей получилось на 25 больше, чем было распилов, значит, первоначально брёвен было 25.

Ответ: 25

Задача 32
. В день рождения дяди Федора почтальон Печкин хочет выяснить, сколько тому лет. Шарик говорит, что дяде Федору больше 11 лет, а кот Матроскин утверждает, что больше 10 лет. Сколько лет дяде Федору, если известно, что ровно один из них ошибся? Ответ обоснуйте.

Решение: Заметим, что если не ошибся Шарик, то не ошибся и Матроскин, что противоречит условию. Значит, Шарик сказал неправду, в отличие от кота Матроскина. Таким образом, дяде Федору больше 10 лет, но не меньше 11., дяде Федору исполнилось 11 лет.

Ответ: 11 лет.

Задача 33

.Математическая логика .(6)

Когда три подруги — Надя, Валя и Маша — вышли гулять, на них были белое, красное и синее платья. Туфли их были тех же трех цветов, но только у Нади цвета туфель и платья совпадали. При этом у Вали ни платье, ни туфли не были синими, а Маша была в красных туфлях. Определите цвет платьев и туфель каждой из подруг.

Подсказка

У Вали белые туфли — почему?

Решение:

У Вали туфли не синие (по условию) и не красные (красные — у Маши), следовательно, у Вали белые туфли; у Нади, таким образом, оставшиеся синие. Это в свою очередь означает, что у Нади — синее платье (по условию, цвета туфель и платья у Нади совпадают). Тогда у Вали — красное платье, а у Маши — белое (поскольку у них по условию туфли и платья разного цвета, причём не синего, так как всё синее — на Наде). Итак: у Нади туфли и платье синего цвета; у Вали туфли белые, платье красное; у Маши туфли красные, платье белое. 1

Ответ: У Нади туфли и платье синего цвета; у Вали туфли белые, платье красное; у Маши туфли красные, платье белое.

Задача 34

В комнате находятся 85 воздушных шаров — красных и синих. Известно, что: 1) по крайней мере один из шаров красный; 2) из каждой произвольно выбранной пары шаров по крайней мере один синий. Сколько в комнате красных шаров? (6)

Подсказка

Подумайте, может ли в комнате быть два красных шара.

Решение:

Поскольку среди двух любых шаров один синий, то двух красных шаров в комнате быть не может. Значит, в комнате находятся 84 синих воздушных шара и 1 красный.

Ответ 1 шар.

Задача 35

Среди 4-х людей нет трех с одинаковым именем, одинаковым отчеством или одинаковой фамилией, но у любых двух людей совпадают либо имя, либо отчество, либо фамилия. Может ли так быть? .(6)

---

Подсказка

Попробуйте написать эти имена.

Решение:

Да, так может быть, например: Иван Иванович Иванов, Иван Петрович Петров, Петр Иванович Петров, Петр Петрович Иванов

Ответ: Иван Иванович Иванов, Иван Петрович Петров, Петр Иванович Петров, Петр Петрович Иванов

ЗАДАЧА 36Сколько трёхзначных чисел можно составить из цифр 2,4,6,8, если цифры в записи числа не повторяются?

Решение: стр. 39 учебника, 4*3*2= 24 трехзначных числа

Задача 37: Сегодня Сереже исполнилось 10 лет, а Вове – 1 год. Каков будет возраст Сережи, когда он станет втрое старше Вовы?

Решение: Серёже-15, Вове 5 через 5 лет

Задача 38: Составьте из цифр 1, 2, 3, 4, 5, 6, 7, 8, 9 магический квадрат, то есть разместите их в таблице 3 × 3 так, чтобы суммы чисел по строкам, столбцам и двум диагоналям были одинаковы.

Решение:



Задача 39: Девочка заменила каждую букву в своем имени ее номером в русском алфавите и получила число 2011533. Как ее зовут? Имеет ли задача однозначный ответ? Почему?

Задача 40: Школьники посадили вдоль дороги (по прямой) 25 деревьев. Расстояние между двумя любыми соседними деревьями одинаковое. Найдите это расстояние, если между крайними деревьями 600 дм.

. Тем более, что подобные задачи мы с детьми решаем на моем математическом кружке в Новых Черемушках.

Решение: 600:24 = 25 дм – расстояние между двумя любыми соседними деревьями

ЗАДАЧА 41

Вася может получить число 100, используя десять двоек, скобки и знаки арифметических действий:

100 = (22 : 2 — 2 : 2) ·  (22 : 2 — 2 : 2)

Улучшите его результат: используйте меньшее число двоек и получите число 100.

В шестом классе вместо двоек были тройки, в седьмом — семерки. Но на решение задачи это никак не влияло.

Решение задачи

Один из вариантов, не самый короткий, предусматривает использование 8 двоек:

(22 — 2) : 2 · (22 — 2) : 2 = 100

Аналогично для троек и семерок:

(33 — 3) : 3 · (33 — 3) : 3 = 100

(77 — 7) : 7 · (77 — 7) : 7 = 100

На занятиях математического кружка в Новых Черемушках мои четвероклассники и даже третьеклассники нашли вариант из 6 двоек:

(222 — 22) : 2 = 100

Аналогично: (333 — 33) : 3 = 100, (777 — 77) : 7 = 100

ЗАДАЧА 42

---

разрежьте фигуру на 3 равные части.

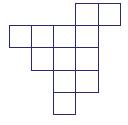
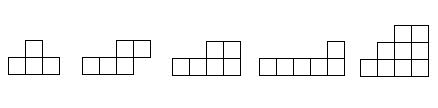
Задача № 43 . Составьте квадрат, используя ровно четыре из пяти изображенных ниже фигур. Каждую из четырех выбранных Вами фигур можно использовать только один раз.



Задача 44 . Без ореха (от дупла до орешника) белка бежит со скоростью 4 м/сек, а с орехом (от орешника до дупла) — со скоростью 2 м/сек. На путь от дупла до орешника и обратно она тратит Шаг 1. Посчитаем, сколько клеточек содержится в фигуре. Их 12.

Шаг 2. Определим, сколько клеточек должна содержать каждая полученная в результате разрезания часть.  12:3 = 4.

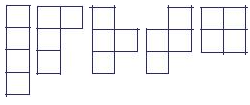
Шаг 3. Нарисуем все возможные комбинации из 4 клеточек. Их я насчитал 5 (не рассматриваем фигуры, где клеточки соединяются только «углом»).



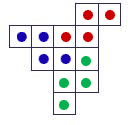
Шаг 4. Исследуем все варианты и отбрасываем те, что не подходят. В итоге получаем возможное решение:



ЗАДАЧА 45:

Как отмерить 8 л воды, находясь около реки и имея два ведра вместимостью 10 л и 6 л? (8 л воды должно получиться в одном ведре).

Решение задачи

Запишем последовательность действий в таблицу, указывая в первом столбце действие, а во втором и третьем – результат, т.е. сколько воды остается в каждом ведре после действия.

Действие	Ведро 10 л	Ведро 6 л
Изначально оба ведра пустые	0	0
Наполним большое ведро из речки	10	0
Перельем из большого в  маленькое 6 л	4	6
Выльем всю воду из маленького	4	0
Перельем из большого в  маленькое всю воду, т.е. 4 л	0	4
Наполним большое ведро из речки	10	4
Отольем из большого ведра столько, чтобы наполнить маленькое до краев, т.е. 2 л.	8	6

---

В результате в большом ведре останется ровно 8 литров.

ЗАДАЧА 46:

Белоснежка вошла в комнату, где вокруг круглого стола стояло 30 стульев. На некоторых из стульев сидели гномы. Оказалось, что Белоснежка не может сесть так, чтобы рядом с ней никто не сидел. Какое наименьшее число гномов могло быть за столом?

(Объясните, как должны были сидеть гномы и почему, если бы гномов было меньше, Белоснежка нашла бы стул, рядом с которым никто не сидит).

Решение задачи

Каждый гном может сделать недоступными для Белоснежки 3 стула — тот, на котором он сидит, а также стулья справа и слева. Поэтому наименьшее число гномов 30 : 3 = 10. Гномы могут сидеть, например, на стульях с номерами 3, 6, 9, … 30 – через каждые два стула на третьем. При таком расположении любой пустой стул оказывается рядом с занятым (либо  справа, либо слева).

Докажем, что при меньшем числе гномов Белоснежка найдет свободный стул без соседей. Пусть гномов за столом 9. Назначим любого гнома старшим и начнем отсчет стульев с него – т.е «старший» гном сидит на стуле №1. При этом Белоснежка уже не сможет занять стулья №30 и №2. Следующий гном должен сесть не дальше, чем на стул № 4, иначе Белоснежка сядет на стул № 3 – и рядом с ней окажутся свободными оба соседних стула — №2 и №4. Рассуждая аналогично, приходим к выводу, что третий гном сядет на стул №7, четвертый – на стул №10 и т.д. Девятому гному достанется стул №25. А это означает, что в распоряжении Белоснежки будут стулья №27, 28 и 29, на любом из которых она сможет расположиться без соседей по бокам.

ЗАДАЧА 47:

Папа, Маша и Яша идут в школу. Пока папа делает 3 шага, Маша делает 5 шагов. Пока Маша делает 3 шага, Яша делает 5 шагов. Маша и Яша посчитали, что вместе они сделали 400 шагов. Сколько шагов сделал папа?

(Напишите решение задачи, а не только ответ).

Решение задачи

Рассмотрим отрезок пути, на котором Маша делает 3 шага, а Яша – 5 шагов. Вместе они делают на таком отрезке 8 шагов. Значит, они прошли 400 : 8 = 50 таких отрезков. И Маша сделала 50 ·  3 = 150 шагов.

Теперь рассмотрим другой отрезок – на котором уже папа делает 3 шага, а Маша – 5 шагов. Таких отрезков было 150 : 5 = 30. Отсюда легко вычислить, сколько шагов сделал папа: 30 ·  3 = 90 шагов.

Ответ: папа сделал 90 шагов

задача 48: 1. На ступеньках дома сидят рядышком мальчик и девочка.

– Я мальчик, – говорит ребёнок с чёрными волосами.

– А я девочка, – говорит ребёнок с рыжими волосами.

Если по крайней мере один из детей говорит неправду, то кто из них мальчик, а кто девочка?

---

Решение

Для двух произвольных высказываний существуют четыре возможные комбинации типа «истина – ложь», а именно:

И – И,   И – Л,   Л – И,   Л – Л.

Первая из них исключается, поскольку в условии оговаривается, что по крайней мере одно из высказываний является ложным. Вторая и третья комбинации также исключается, потому что если один ребёнок врал, то и другой не мог говорить правду, иначе мы бы имели дело с двумя мальчиками или с двумя девочками, что противоречит условию. Следовательно, оба говорили неправду.

Итак, у мальчика рыжие волосы, а у девочки чёрные.

Задача 49:

Можно ли расставить по окружности 20 красных и несколько синих фишек так, чтобы в каждой точке, диаметрально противоположной красной фишке, стояла синяя и никакие две синие фишки не стояли рядом?

Решение

Из условия следует, что красные и синие фишки должны чередоваться (на окружности), значит, всего их 40. Фишки по окружности размещаются равномерно в том смысле, что две диаметрально противоположные фишки делят множество оставшихся 38 фишек на две части по 19 фишек, расположенные в одной и другой полуокружностях относительно двух данных фишек. Это так, потому что согласно условию, каждая фишка имеет диаметрально противоположную. Диаметрально противоположные фишки имеют разный цвет, поэтому 19 фишек, расположенные в одной из полуокружностей должны чередоваться по цвету и начинаться и заканчиваться фишками разного цвета, что невозможно при нечётном 19. Следовательно, указанная в задаче расстановка фишек не возможна.

Ответ: нельзя.

Задача 50:

Разбирается дело Брауна, Джонса и Смита. Один из них совершил преступление. В процессе расследования каждый из них сделал по два заявления.

Браун: «Я не делал этого. Джонс не делал этого.»

Джонс: «Браун не делал этого. Смит сделал это.»

Смит: «Я не делал этого. Браун сделал это.»

Было установлено далее, что один из них дважды солгал, другой дважды сказал правду, третий – раз солгал, раз сказал правду. Кто совершил преступление?

Решение

Если вор – Смит, то и Браун, и Джонс оба сказали правду. Если вор – Джонс, то и Браун, и Смит одновременно сказали и правду, и ложь. Итак, Браун – преступник. Джонс оба раза солгал, Смит оба раза сказал правду, Браун один раз солгал, второй раз сказал правду.

Задача 51:

Шурик, Трус, Балбес и Бывалый участвовали в турнире по домино и заняли первые четыре места. Сумма мест, занятых Шуриком, Трусом и Балбесом, равна 6, сумма мест Труса и Бывалого тоже равна 6. Какое место занял каждый из них, если Трус занял более высокое место, чем Шурик? Объясните, как вы получили ответ.

---