Файл: Сборник олимпиадных задач по математике для 5 класса.docx

Сборник олимпиадных задач по математике

для 5 класса

( с ответами и решениями)

Составитель: учитель математики высшей категории

Максимова Н.М. ГБОУ ШКОЛА № 2036 г Москва

Содержание:

1. Разные задачи............................................................

2.Метод графов..............................................................

3.Табличный способ.......................................................

4.Задачи на переливание...............................................

5.Задачи на взвешивание..............................................

6.Задания на восстановление записей

вычисления.................................................................

7. Олимпиадные задачи ( дистанционные олимпиады,

конкурс "Кенгуру", "Математическая карусель")......

ГЛАВА 1: Разные задачи

Задача 1:

В пещере старый пират разложил свои сокровища в 3 цветных сундука, стоящих вдоль стены: в один - драгоценные камни, а в другой - золотые монеты, а в третий - оружие. Он помнит, что :
- красный сундук правее, чем драгоценные камни
- оружие правее, чем красный сундук.

В сундуке какого цвета лежит оружие, если зелёный сундук стоит левее, чем синий?

Решение :

ДК - зелёный
ЗC - красный
О - синий


Задача 2 :
Девять осликов за 3 дня съедают 27 мешков корма.
Сколько корма надо пяти осликам на 5 дней?

Решение :

1 шаг 9 осликов в 1 день - 27 : 3= 9м.
2 шаг 1 ослик в 1 день - 9 : 9 = 1 м.
3 шаг 5 осликов в 1 день - 5 * 1 = 5 м.
4 шаг 5 осликов за 5 дней - 5 * 5 = 25 м.

Задача 3 :

Кенгуру мама прыгает за 1 секунду на 3 метра, а её маленький сынишка прыгает на 1 метр за 0,5 секунды.
Они одновременно стартовали от бассейна к эвкалипту по прямой.
Сколько секунд мама будет ждать сына под деревом, если расстояние от бассейна до дерева 240 метров

Решение :
1 шаг 240 : 3 = 80 (с) скакала мама Кенгуру
2 шаг сын за 0,5 с - 1 м, за 1 с - 2 м
3 шаг 80 * 2 = 160 (м) проскачет кенгурёнок за 80 с
4 шаг 240 - 160 = 80 (м) осталось проскакать кенгурёнку когда
мама уже под эвкалиптом
5 шаг 80 : 2 = 40 (с)
Ответ: 40 секунд.

Задача 4 :

---

На скотном дворе гуляли гуси и поросята.
Мальчик сосчитал количество голов, их оказалось 30, а затем он сосчитал количество ног, их оказалось 84.
сколько гусей и сколько поросят было на школьном дворе?

Решение :
1 шаг Представьте, что все поросята подняли по две ноги вверх
2 шаг на земле осталось стоять 30 * 2 = 60 ног
3 шаг подняли вверх 84 - 60 = 24 ноги
4 шаг подняли 24 : 2 = 12 поросят
5 шаг 30 - 12 = 18 гусей
Ответ: 12 поросят и 18 гусей.

Задача 5

Инженер ежедневно приезжал на станцию в одно и то же время, и в то же время за ним подъезжала машина, на которой он ехал на завод.
Однажды инженер приехал на станцию на 55 мин раньше обычного.
Сразу пошел навстречу машине и приехал на завод на 10 мин раньше, чем обычно.
Во сколько раз скорость инженера меньше скорости машины?

Решение:

За 10 мин машина проходит путь, равный двойному расстоянию от станции до места встречи инженера с машиной.
Значит, путь от станции до места встречи машина проходит за 5 мин.
На месте встречи машина была за 5 мин до времени обычного приезда инженера на станцию, значит, путь от станции до места встречи инженер шел 55 мин - 5 мин = 50 мин.
Следовательно, скорость инженера в 50 : 5 = 10 раз меньше скорости машины.

Задача 6

В триседьмом царстве живут драконы.
У каждого дракона одна, две или три головы,
а) Может ли у 40 % драконов быть 60 % голов?
б) Может ли у 40 % драконов быть 70 % голов?

Решение:

а) Покажем, что у 40% драконов может быть 60% голов.
Пусть в этом царстве живет 100 драконов: 40 драконов с одной головой, 20 – с двумя головами и 40 – с тремя.
Тогда число голов у всех драконов равно
40 • 1 + 20 • 2 + 40 • 3 = 200.
При этом все 40 трехглавых драконов, что составляет 40% от общего числа драконов, имеют 40 • 3 = 120 голов, что составляет
120/200 • 100% = 60% от общего числа голов.
б) Пусть число драконов равно х, а общее число голов у них равно у.
Предположим, что какие-то 40% драконов имеют 70% голов.
Тогда, поскольку каждый из этих драконов имеет не более трех голов, то 0,7у = 3 • 0,4х.
С другой стороны, поскольку остальные 60% драконов имеют 30% голов и у каждого из них не менее одной головы, то 0,6х = 0,3y.
Но эти неравенства не могут выполняться одновременно, так как они равносильны соответственно 7у = 12х и 12x = 6у.
Поэтому у 40% драконов не может быть 70% голов.

Задача 7

---

В пещере старый пират разложил свои сокровища в 3 цветных сундука, стоящих вдоль стены: в один - драгоценные камни, а в другой - золотые монеты, а в третий - оружие. Он помнит, что :
- красный сундук правее, чем драгоценные камни
- оружие правее, чем красный сундук.

В сундуке какого цвета лежит оружие, если зелёный сундук стоит левее, чем синий?

Решение :

ДК - зелёный
ЗC - красный
О - синий

Задача 8

Девять осликов за 3 дня съедают 27 мешков корма.
Сколько корма надо пяти осликам на 5 дней?

Решение :

1 шаг 9 осликов в 1 день - 27 : 3= 9м.
2 шаг 1 ослик в 1 день - 9 : 9 = 1 м.
3 шаг 5 осликов в 1 день - 5 * 1 = 5 м.
4 шаг 5 осликов за 5 дней - 5 * 5 = 25 м.

Задача 9

Кенгуру мама прыгает за 1 секунду на 3 метра, а её маленький сынишка прыгает на 1 метр за 0,5 секунды.
Они одновременно стартовали от бассейна к эвкалипту по прямой.
Сколько секунд мама будет ждать сына под деревом, если расстояние от бассейна до дерева 240 метров

Решение :

1 шаг 240 : 3 = 80 (с) скакала мама Кенгуру
2 шаг сын за 0,5 с - 1 м, за 1 с - 2 м
3 шаг 80 * 2 = 160 (м) проскачет кенгурёнок за 80 с
4 шаг 240 - 160 = 80 (м) осталось проскакать кенгурёнку когда
мама уже под эвкалиптом
5 шаг 80 : 2 = 40 (с)
Ответ: 40 секунд.

Задача 10

На скотном дворе гуляли гуси и поросята.
Мальчик сосчитал количество голов, их оказалось 30, а затем он сосчитал количество ног, их оказалось 84.
сколько гусей и сколько поросят было на школьном дворе?

Решение :

1 шаг Представьте, что все поросята подняли по две ноги вверх
2 шаг на земле осталось стоять 30 * 2 = 60 ног
3 шаг подняли вверх 84 - 60 = 24 ноги
4 шаг подняли 24 : 2 = 12 поросят
5 шаг 30 - 12 = 18 гусей
Ответ: 12 поросят и 18 гусей.

ЗАДАЧА 11

Среди 100 одинаковых на вид монет есть несколько фальшивых. Все фальшивые монеты весят одинаково, все настоящие - тоже, фальшивая монета легче настоящей. Имеются также весы (с двумя чашами без стрелки), на каждой чашке умещается только по одной монете. При этом весы слегка испорчены: если монеты разного веса, перевешивает более тяжёлая монета, а если одинакового - перевесить может любая чашка. Как с помощью этих весов найти хотя бы одну фальшивую монету? 

Ответ: Разделим монетки на 33 кучки по 3 монетки + 1 монетка.
Каждое трио взвешиваем между собой, получим 3 неравенства, в результате которых увидим, либо каждая монетка будет по одному разу весить меньше от других двух, либо два раза будет весить меньше других двух.
1>2 (возможны такие варианты: н=н, ф=ф, 2-фальшивка)

---

1<3 (н=н, ф=ф, 1- фальшивка)
2>3 (н=н, ф=ф, 3- фальшивка)
такое возможно, если все три монетки имеют одинаковый вес вежду собой, то есть из них откладываем в сторонку любую одну
1<2(н=н,ф=ф,1-ф)
1<3(н=н,ф=ф,1-ф)
2>3(н=н,ф=ф,3-ф)
У 1 больше вероятностьть оказаться фальшивой, так что ее и откладываем.
И так проделываем с каждой из 33-х кучек, в результате отложим 11 монет +1, которая не попала ни в одну из кучек.
 Эти 12 монет опять разделям на 4 кучки по 3 монетки, проделываем те же манипуляции, в результате получим 4 монетки, разделяем на 1 кучку+1, та монетка из кучки, которая окажется легче, вновь откладываем и сравниваем с одинокой монеткой. Та, которая легче и будет фальшивой.

ГЛАВА П Метод графов

Один из способов решения задач типа «Кто есть кто?» - метод графов. 
Граф – это несколько точек, часть которых соединены друг с другом отрезками или стрелками (в этом случае граф называется ориентированным). 


Рассмотрим метод графов на примере решения задачи:
Жила-была одна дружная семья: мама, папа и сын. Они все любили делать вместе. Но вот мультфильмы любили разные: «Ну, погоди!», «Покемоны», «Том и Джерри». Определите, какой мультфильм любит каждый из них, если мама, папа и любитель мультфильма «Покемоны» никогда не унывают, а папа и любитель мультфильма «Том и Джерри» делают зарядку по утрам? 

Решение:

Рассмотрим множество людей: мама, папа, сын и множество мультфильмов «Ну, погоди!», «Покемоны», «Том и Джерри». Обозначим элементы этих двух множеств точками: 




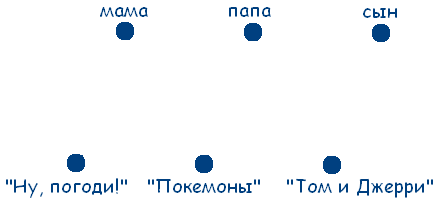
Если точке из одного множества соответствует точка другого множества, будем соединять эти точки сплошной линией, если не соответствует – то штриховой. 
Заметим, что по условию задачи у человека только один любимый мультфильм. 
Учитывая данные задачи, получаем следующую схему:




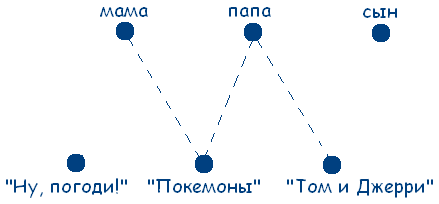
Из условия задачи следует, что нужно найти единственно возможное соответствие между элементами двух множеств. 
Правило: если какая-то точка оказывается соединенной с двумя точками другого множества штриховыми линиями, то с третьей точкой она должна быть соединена сплошной. 

---

Поэтому граф на рисунке будет выглядеть следующим образом:




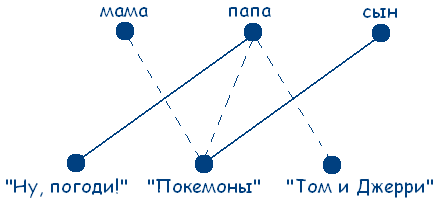
Теперь мы установили, что папа любит мультфильм «Ну, погоди!», сын – «Покемоны». В обеих множествах остается только по одной точке, следовательно мама любит мультфильм «Том и Джерри». Задача решена. 
Таким же способом можно находить соответствие между тремя множествами. Тогда при решении мы можем получить треугольники трех видов: 
а) все стороны являются сплошными отрезками (решение задачи); 
б) одна сторона – сплошной отрезок, а две другие – штриховые; 
в) все стороны – штриховые отрезки. 
Таким образом, нельзя получить треугольник, у которого бы две стороны были сплошными отрезками, а третья – штриховой отрезок. 
3>

---