ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 06.04.2021
Просмотров: 1447
Скачиваний: 4
ЕНЕРГЕТИЧНІ
ТА
ТЕПЛОТЕХНІЧНІ
ПРОЦЕСИ
Й
УСТАТКУВАННЯ
( )
(
)
0
2
;
2
;
lim
10
п
2
,
1
1
,
1
10
п
1
1
=
=
⇒
∞
=
∞
→
C
C
x
x
C
C
x
y
x
;
( )
.
;
0
;
1
lim
10
п
10
п
1
1
∞
→
→
=
∞
→
C
C
C
C
x
y
x
Из
совместного
решения
1
=
y
и
( )
1
x
y
′
следует
,
что
точки
А
и
В
пересечения
( )
1
x
y
и
1
не
зависят
от
и
,
следовательно
,
существуют
для
всех
.
Координаты
А
и
В
(
рис
. 2)
=
y
1
10
п
−
⋅
C
C
1
10
п
−
⋅
C
C
(
)
[
]
(
)
1
1
2
0
3
2
2
0
0
,
−
−
−
±
=
′
h
h
h
x
B
A
.
Кратному
нулю
1
2
,
1
1
,
1
=
=
x
x
соответствует
область
существования
нулей
H
def
K
h
h
C
C
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
−
≥
−
1
2
0
0
10
п
1
1
2
и
квазинулевому
участку
упругой
характеристике
опоры
(
рис
. 4)
соответствует
П
10
п
2
K
C
C
≥
.
Рис
. 4.
Качественная
зависимость
упругой
характеристики
опоры
от
безразмерных
координат
Из
симметрии
( )
1
x
y
относительно
1
1
=
x
следует
симметрия
1
,
1
x
и
2
,
1
x
относительно
1
1
=
x
.
Линии
равного
уровня
const
1
=
x
на
плоскости
(
)
1
10
п
0
2
,
−
⋅
α
C
C
показаны
на
рис
. 5.
8’2012
135
ЕНЕРГЕТИЧНІ
ТА
ТЕПЛОТЕХНІЧНІ
ПРОЦЕСИ
Й
УСТАТКУВАННЯ
Рис
. 5.
Линии
равного
уровня
на
плоскости
параметров
упругой
опоры
Полученные
зависимости
позволят
разрабатывать
опоры
с
управляемой
квазинулевой
жесткостью
для
подшипников
высокоскоростных
роторных
систем
,
которые
имеют
максимально
возможную
статическую
жесткость
на
нерабочих
режимах
и
минимально
возможную
жесткость
опоры
на
рабочих
,
что
обеспечит
максимально
возможную
динамическую
жесткость
и
,
следовательно
,
точность
работы
высокоскоростных
роторных
систем
с
сохранением
требуемого
ресурса
.
Список
литературы
: 1.
Гапонов
,
В
.
С
.
Аналитический
обзор
литературы
по
вопросам
конструктивного
обеспечения
динамической
устойчивости
высокоскоростных
роторных
систем
[
Текст
] /
В
.
С
.
Гапонов
,
А
.
В
.
Гайдамака
,
Е
.
Ю
.
Гладыщева
//
Машиноведение
и
САПР
.
Вестник
НТУ
«
ХПИ
»:
Сб
.
науч
.
трудов
. –
Харьков
:
НТУ
«
ХПИ
». – 2010. –
№
19. –
С
. 39-44.
2.
Патент
на
винахід
62934
Україна
.
Пасивна
віброзахисна
система
з
керованою
квазінульовою
жорсткістю
/
В
.
С
.
Гапонов
,
П
.
М
.
Калінін
. – 2004. –
Бюл
.
№
1.
3.
Гапонов
,
В
.
С
.
Упругая
опора
подшипников
ротора
с
управляемым
изменением
квазинулевой
жесткости
[
Текст
] /
В
.
С
.
Гапонов
,
А
.
И
.
Наумов
//
Вісник
НТУ
«
ХПІ
». – 2010. –
№
33. –
С
. 68-73.
©
Гапонов
В
.
С
.,
Наумов
А
.
И
.,
Остапчук
Ю
.
А
., 2012
Поступила
в
редколлегию
15.02.12
8’2012
136
ЕНЕРГЕТИЧНІ
ТА
ТЕПЛОТЕХНІЧНІ
ПРОЦЕСИ
Й
УСТАТКУВАННЯ
УДК
621.51:532.556.4
В
.
П
.
ГЕРАСИМЕНКО
,
д
-
р
техн
.
наук
;
проф
.
НАКУ
«
ХАИ
»,
Харьков
;
А
.C.
ТКАЧУК
,
магистр
НАКУ
«
ХАИ
»,
Харьков
;
А
.
А
.
ЯЦЫШИН
,
магистр
НАКУ
«
ХАИ
»,
Харьков
О
ПОЛЯРАХ
ПЛОСКИХ
ДИФФУЗОРОВ
Рассмотрены
основные
режимы
течения
в
дозвуковых
плоских
диффузорах
.
Предложено
представлять
характеристики
диффузоров
в
форме
поляр
.
Такая
форма
характеристики
удобная
для
практического
использования
при
формировании
облика
диффузора
с
оптимальными
параметрами
.
Розглянуто
основні
режими
течії
у
дозвукових
плоских
дифузорах
.
Запропоновано
подавати
характеристики
дифузорів
у
формі
поляр
.
Така
форма
характеристик
зручна
для
практичного
використання
у
формуванні
обрису
дифузора
з
оптимальними
параметрами
.
Fundamental air current regimes in subsonic straight-wall diffusers have been considered. Diffuser-polar
characteristic curves are proposed. This characteristic shape is convenient for choice diffuser appearance with
optimization parameters.
Диффузоры
–
простейшие
преобразователи
энергии
в
потоках
газов
,
широко
применяют
в
турбомашинах
и
энергетических
установках
[1–4].
Они
должны
обладать
оптимальными
качествами
согласно
их
функциональному
назначению
в
конкретных
условиях
применения
,
удовлетворяя
при
этом
определенным
требованиям
-
критериям
оптимальности
:
иметь
максимальное
значение
КПД
или
коэффициента
повышения
давления
и
т
.
п
.
Такие
требования
могут
быть
удовлетворены
или
путем
специального
выбора
геометрических
размеров
под
заданные
условия
течения
,
или
путем
выбора
режима
течения
на
характеристике
диффузора
с
заданными
геометрическими
размерами
.
И
в
одном
и
в
другом
случаях
указанные
требования
достигаются
при
безотрывном
течении
или
при
небольшом
неустойчивом
отрыве
[5–7].
Развитие
отрывных
явлений
в
диффузорах
имеет
достаточно
сложный
характер
в
зависимости
от
типа
диффузора
:
плоский
прямолинейный
или
криволинейный
,
конический
,
кольцевой
или
осерадиальный
и
т
.
д
. [8–12].
Картина
отрыва
потока
даже
в
простейших
плоских
диффузорах
с
прямолинейными
стенками
имеет
трехмерный
характер
и
существенно
отличается
от
классического
отрыва
внешних
течений
.
Для
внутренних
течений
в
диффузорных
каналах
обнаружено
четыре
различные
состояния
по
отрыву
–
четыре
режима
течения
[13]:
без
заметного
отрыва
;
с
большим
неустойчивым
отрывом
; c
двумерным
отрывом
;
со
струйным
течением
.
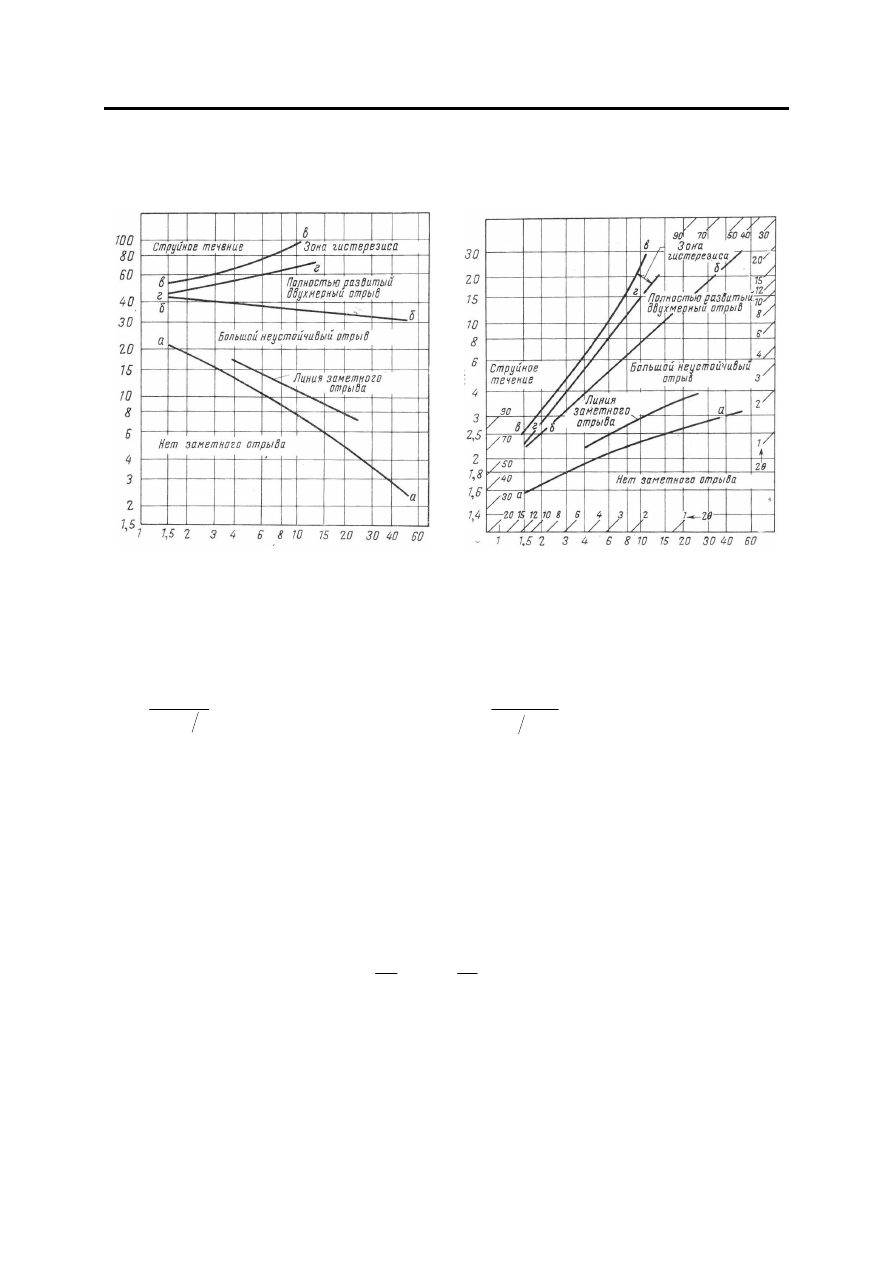
Перечисленным
режимам
течения
соответствуют
определенные
области
на
обобщенных
характеристиках
плоских
диффузоров
(
рис
. 1),
границы
между
которыми
показаны
примерно
,
ибо
их
положение
может
быть
смещено
малыми
изменениями
условий
в
потоке
.
Обобщенные
характеристики
плоских
диффузоров
(
рис
. 1)
являются
результатом
подробных
систематизированных
расчетно
-
экспериментальных
исследований
дозвуковых
диффузоров
,
выполненных
по
специальной
программе
в
Стэндфордском
университете
(
США
) [6–11, 13].
Наряду
с
представленными
характеристиками
,
где
показаны
области
,
соответствующие
различным
режимам
течения
,
выделено
три
режима
отрыва
:
неустойчивый
отрыв
;
перемежающийся
отрыв
и
начинающийся
отрыв
[11].
Получены
также
усовершенствованные
корреляции
отрыва
[8, 13],
положенные
в
основу
определения
границ
срыва
компрессорных
ступеней
[14, 15].
Практический
интерес
при
создании
диффузоров
в
технике
представляют
8’2012
137
ЕНЕРГЕТИЧНІ
ТА
ТЕПЛОТЕХНІЧНІ
ПРОЦЕСИ
Й
УСТАТКУВАННЯ
безотрывные
режимы
или
при
небольшом
неустойчивом
отрыве
[2–7].
Поэтому
определение
характеристик
диффузора
при
безотрывном
течении
–
актуальная
задача
.
2
θ
L
/
A
1
A
2
/
A
1
L
/
A
1
а
)
б
)
Рис
. 1.
Области
режимов
течения
на
характеристиках
диффузоров
Целью
данной
статьи
является
разработка
метода
определения
характеристик
диффузоров
с
безотрывным
течением
.
Такие
характеристики
удобны
при
использовании
в
форме
поляр
,
связывающих
коэффициент
повышения
давления
2
2
1
1
1
2
W
P
P
Cp
ρ
−
=
и
КПД
η
=
Ср
/
Ср
ид
,
где
(
)
2
1
2
ид
1
1
A
A
Cp
−
=
–
коэффициент
идеального
повышения
давления
,
с
заданной
геометрией
диффузора
.
Установлено
[9],
что
максимум
КПД
плоских
диффузоров
достигается
при
угле
раскрытия
2
θ
≈
7°,
а
Ср
max
–
при
несколько
больших
углах
и
наличии
небольшого
отрыва
.
Анализ
течения
в
плоских
диффузорах
позволяет
достаточно
наглядно
описать
основные
закономерности
их
режимов
работы
.
Безотрывные
режимы
течения
или
с
неустойчивым
перемежающимся
отрывом
[9]
в
простейших
плоских
диффузорах
с
прямолинейными
стенками
определяются
,
главным
образом
,
общей
геометрией
диффузора
с
тремя
безразмерными
параметрами
:
углом
раствора
диффузора
2
θ
;
отношением
площадей
выхода
и
входа
A
2
/
A
1
и
относительной
длинной
L
/
A
1
,
среди
которых
два
из
них
являются
независимыми
,
а
третий
–
зависимый
по
формуле
:
θ
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
=
−
tg
2
1
1
1
2
A
L
A
A
. (1)
Наличие
двух
независимых
переменных
для
плоских
диффузоров
,
в
пространстве
которых
удобно
представлять
их
характеристики
по
режимам
течения
(
рис
. 1),
определяется
физической
природой
развития
течения
с
возникновением
отрывных
явлений
в
пристенных
пограничных
слоях
.
А
именно
:
нарастание
пограничного
слоя
и
его
отрыв
может
происходить
как
за
счет
роста
градиента
давления
при
увеличении
угла
раскрытия
диффузора
,
так
и
за
счет
утолщения
8’2012
138
ЕНЕРГЕТИЧНІ
ТА
ТЕПЛОТЕХНІЧНІ
ПРОЦЕСИ
Й
УСТАТКУВАННЯ
пограничного
слоя
на
стенке
при
увеличении
длины
.
В
практической
ситуации
оба
эффекта
проявляются
одновременно
.
В
связи
с
этим
при
пояснении
причин
и
механизмов
основных
гидравлических
потерь
в
таких
диффузорах
обычно
называют
[2, 3]:
потери
,
обусловленные
расширением
канала
–
диффузорностью
;
потери
на
трение
об
ограничивающие
стенки
,
а
также
потери
с
выходной
скоростью
из
диффузора
.
Дополнительным
источником
потерь
,
кроме
названных
,
может
быть
загромождение
проходного
сечения
на
входе
в
диффузор
пограничным
слоем
в
виде
параметра
[9]
1
*
1
2
A
δ
,
где
–
толщина
вытеснения
пограничного
слоя
на
боковой
стенке
на
входе
в
диффузор
.
При
сравнительно
тонком
пограничном
слое
на
входе
*
1
δ
01
,
0
2
1
*
1
≤
δ
A
2
таким
загромождением
можно
пренебречь
,
что
соответствует
условию
не
смыкания
пограничных
слоев
на
противоположных
стенках
и
существованию
однородного
одномерного
потенциального
ядра
основного
потока
вне
пограничного
слоя
,
оказывающего
влияние
на
этот
слой
на
стенках
.
Предположение
о
существовании
равномерного
потенциального
ядра
используют
[5–9]
при
разработке
методов
расчета
характеристик
диффузоров
,
построенных
на
двухслойном
подходе
модели
Л
.
Прандтля
о
вязко
-
невязкостном
взаимодействии
.
Когда
ядро
потока
рассматривают
как
течение
идеальной
жидкости
без
проявления
вязкости
,
а
течение
в
пограничных
слоях
на
ограничивающих
стенках
учитывают
с
помощью
интегральных
параметров
пограничного
слоя
на
основе
закона
сохранения
импульсов
.
Уравнение
,
связывающее
местную
скорость
в
одномерном
ядре
потока
и
толщину
вытеснения
пограничного
слоя
на
стенке
с
заданными
условиями
на
входе
,
получают
для
установившегося
течения
в
виде
уравнения
сохранения
суммарного
массового
расхода
через
любое
поперечное
сечение
диффузора
[13].
Такой
подход
,
в
общем
,
обеспечивает
удовлетворительную
точность
расчета
характеристик
плоских
диффузоров
[9].
Однако
применение
его
для
расчета
характеристик
конических
и
осерадиальных
кольцевых
диффузоров
не
представляется
возможным
из
-
за
отсутствия
интегральных
соотношений
трехмерного
пограничного
слоя
.
Вместе
с
тем
,
даже
для
плоских
диффузоров
теория
пограничного
слоя
,
позволяющая
определять
касательные
напряжения
на
поверхности
стенок
,
справедлива
только
для
безотрывного
течения
,
поэтому
существуют
трудности
в
расчете
сопротивления
движению
при
отрыве
потока
.
Более
того
,
для
турбулентных
течений
при
больших
автомодельных
числах
Re,
строго
говоря
,
уравнения
Навье
-
Стокса
не
представляют
собой
замкнутую
систему
,
а
поэтому
требуются
дополнительные
предположения
[4],
основанные
часто
на
квалификации
исследователя
или
экспериментах
.
В
этой
связи
целесообразен
поиск
путей
упрощенного
описания
характеристик
диффузоров
с
достаточной
точностью
для
выбора
оптимальных
геометрических
размеров
.
Двухзонный
подход
в
расчете
характеристик
плоских
диффузоров
оказывается
приемлемым
при
толстых
турбулентных
пограничных
слоях
на
противоположных
стенках
диффузора
,
так
как
турбулентные
профили
скорости
выравниваются
на
внешней
границе
пограничного
слоя
и
потери
полного
давления
вдоль
этой
границы
обычно
незначительны
.
С
другой
стороны
при
толстых
пограничных
слоях
на
входе
в
диффузор
параметр
1
*
1
2
A
δ
может
быть
рассмотрен
как
дополнительная
переменная
[5, 13].
Подобная
ситуация
имеет
практическое
значение
в
случае
расположения
диффузора
за
длинным
трубопроводом
или
иным
устройством
,
а
также
для
кольцевых
диффузоров
в
системе
турбомашин
.
Для
однозначности
описания
режимов
течения
необходимо
соблюдать
также
критерии
гидродинамического
подобия
[5]
по
числам
Рейнольдса
и
Маха
или
исключать
их
влияние
в
области
автомодельности
.
Числа
8’2012
139