ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 06.04.2021
Просмотров: 1446
Скачиваний: 4
ЕНЕРГЕТИЧНІ
ТА
ТЕПЛОТЕХНІЧНІ
ПРОЦЕСИ
Й
УСТАТКУВАННЯ
Рейнольдса
должны
находится
в
диапазоне
3
1
1
10
6
Re
⋅
>
ν
=
A
W
,
а
числа
Маха
для
несжимаемой
жидкости
должны
соответствовать
дозвуковому
течению
,
что
при
M
W
1
< 0,7…0,8
с
учетом
уменьшения
его
вдоль
диффузора
практически
не
оказывает
влияния
на
режим
течения
[5].
Таким
образом
,
при
соблюдении
гидродинамического
подобия
и
условий
на
входе
характеристики
простейших
плоских
безотрывных
диффузоров
однозначно
определяется
их
геометрическими
параметрами
: 2
θ
,
A
2
/
A
1
,
L
/
A
1
.
Подтверждением
данного
утверждения
являются
результаты
расчетов
характеристик
плоских
безотрывных
диффузоров
по
двухзонной
модели
потока
,
состоящего
из
ядра
невязкой
жидкости
и
пограничных
слоев
на
ограничивающих
стенках
диффузора
[13].
Удовлетворительное
совпадение
результатов
расчета
с
экспериментальными
данными
свидетельствует
об
однозначном
соответствии
изменения
параметров
в
невязком
ядре
жидкости
в
диффузоре
с
заданными
геометрическими
параметрами
2
θ
,
A
2
/
A
1
,
L
/
A
1
согласно
уравнениям
Бернулли
и
массового
расхода
,
а
также
формированию
турбулентного
пограничного
слоя
на
боковых
стенках
диффузора
с
соответствующими
его
интегральными
характеристиками
на
основе
законов
сохранения
импульсов
и
массы
.
Следовательно
определенным
геометрическим
параметрам
плоского
дозвукового
безотрывного
диффузора
должны
соответствовать
аэродинамические
параметры
:
Ср
и
η
диффузора
.
Наличие
такого
соответствия
свидетельствует
о
возможности
представления
характеристики
диффузора
в
форме
поляры
–
связи
Ср
,
КПД
или
потерь
с
геометрическими
параметрами
.
Поляра
диффузора
позволяет
выбирать
оптимальные
его
геометрические
параметры
на
стадии
формирования
облика
при
проектировании
или
согласовании
характеристик
с
другими
примыкающими
к
нему
элементами
конструкции
,
т
.
е
.
решать
обратную
аэродинамическую
задачу
в
отличии
от
решения
прямой
задачи
,
для
которой
требуются
трудоемкие
вычислительные
комплексы
[4],
или
приходится
решать
задачу
о
вязко
-
невязкостном
взаимодействии
.
Связь
коэффициента
повышения
давления
Ср
с
КПД
диффузора
η
=
Cp
/
Cp
ид
или
коэффициентом
потерь
полного
давления
2
2
1
1
2
2
*
1
W
P
P
ρ
−
=
ξ
вытекает
из
уравнения
Бернулли
:
ξ
−
−
=
2
1
2
2
1
W
W
Cp
, (2)
где
,
согласно
уравнению
расхода
для
несжимаемой
жидкости
,
первые
два
слагаемых
правой
части
представляют
собой
Cp
ид
–
идеальный
коэффициент
повышения
давления
(
)
2
1
2
2
1
2
2
ид
1
1
1
A
A
W
W
Cp
−
=
−
=
, (3)
откуда
(
)
ид
1
Cp
η
−
=
ξ
. (4)
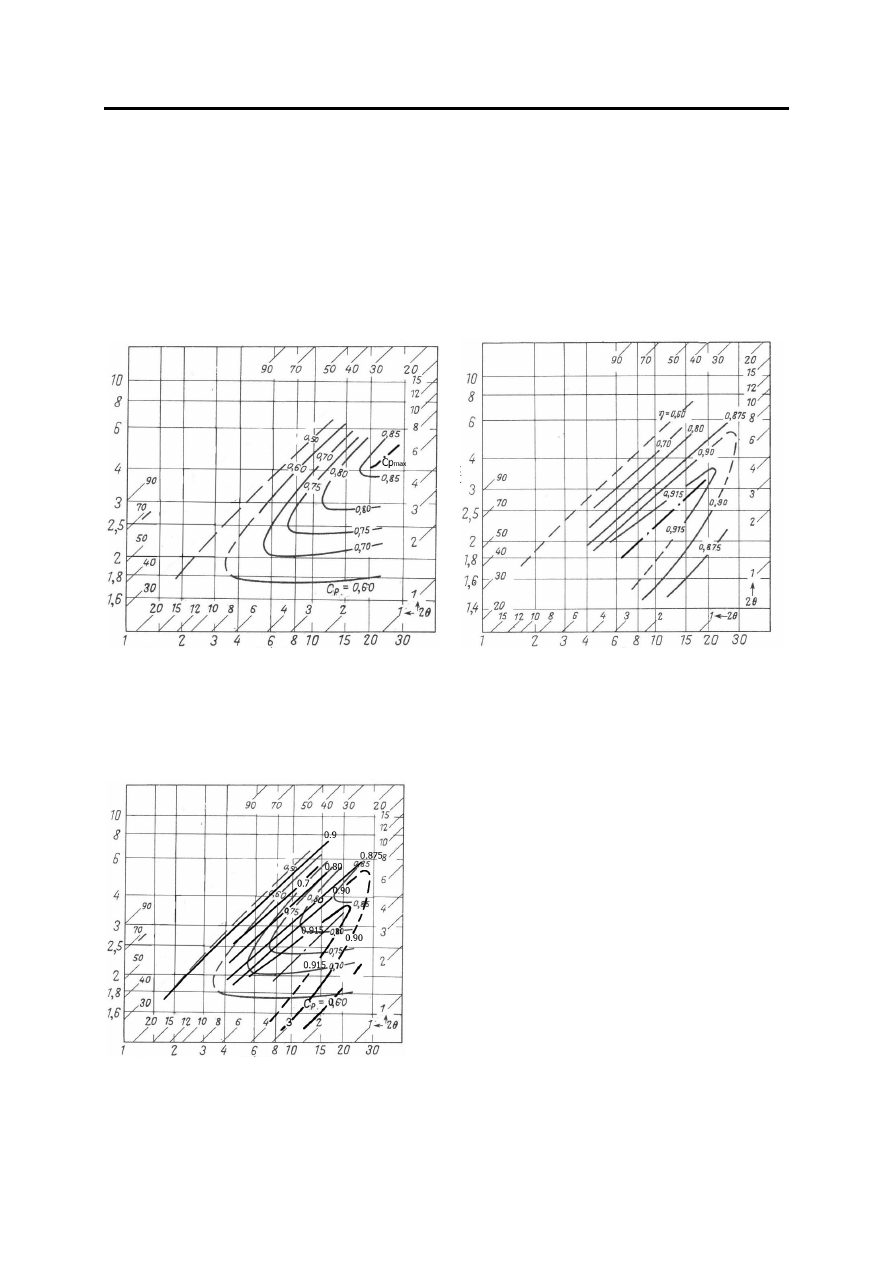
Зависимости
коэффициентов
Ср
и
η
от
геометрических
параметров
диффузоров
достаточно
наглядно
представлены
на
рис
. 2,
где
правая
нижняя
часть
рисунков
соответствует
безотрывным
режимам
течения
при
небольших
углах
раствора
диффузоров
2
θ
< 8
°
.
Из
рис
. 2
а
видно
,
что
в
этой
части
линии
Ср
= const
изображаются
примерно
горизонталями
A
2
/
A
1
= const
согласно
соотношению
(3).
С
ростом
A
2
/
A
1
и
угла
2
θ
увеличение
Ср
происходит
вплоть
до
линии
Ср
max
,
которая
достигается
примерно
8’2012
140
ЕНЕРГЕТИЧНІ
ТА
ТЕПЛОТЕХНІЧНІ
ПРОЦЕСИ
Й
УСТАТКУВАННЯ
при
значении
угла
раствора
диффузора
2
θ
≈
8
°
.
Дальнейший
рост
угла
раствора
диффузора
приводит
к
понижению
Ср
вследствие
развития
отрыва
потока
.
Аналогичные
изменения
наблюдаются
и
с
значениями
КПД
на
рис
. 2
б
при
росте
угла
раствора
диффузора
,
соответствующему
перемещению
по
диагонали
рис
. 2
б
из
правого
нижнего
угла
в
направлении
к
левому
верхнему
углу
,
где
в
начале
наблюдается
рост
КПД
,
а
после
достижения
η
max
при
угле
2
θ
≈
7
°
–
понижение
.
Таким
образом
,
из
рис
. 2
а
,
б
видно
,
что
направление
роста
угла
раствора
2
θ
соответствует
градиентам
коэффициентов
повышения
давления
и
КПД
.
A
2
/
A
1
L
/
A
1
A
2
/
A
1
L
/
A
1
а
)
б
)
max
η
Рис
. 2.
Топограммы
коэффициента
повышения
давления
(
а
)
и
коэффициента
полезного
действия
(
б
)
плоских
дозвуковых
диффузоров
A
2
/
A
1
L
/
A
1
Рис
. 3.
Поляра
диффузоров
Совмещение
этих
двух
рисунков
путем
их
наложения
друг
на
друга
позволяет
установить
связь
коэффициентов
Ср
и
η
в
пространстве
геометрических
параметров
: 2
θ
,
A
2
/
A
1
,
L
/
A
1
,
что
соответствует
поляре
диффузора
(
рис
. 3).
Ввиду
того
,
что
линия
,
соответствующая
максимальному
КПД
на
рис
. 2
б
,
достигается
при
угле
раствора
диффузора
2
θ
≈
7
°
,
то
нанесение
данной
линии
на
рис
. 2
а
позволяет
определить
геометрические
размеры
диффузора
2
θ
,
A
2
/
A
1
,
L
/
A
1
и
коэффициент
повышения
давления
Ср
при
η
max
.
Аналогично
поляра
диффузоров
(
см
.
рис
. 3)
позволяет
определить
сочетание
геометрических
параметров
плоского
диффузора
с
необходимыми
значениями
коэффициента
повышения
давления
Ср
и
8’2012
141
ЕНЕРГЕТИЧНІ
ТА
ТЕПЛОТЕХНІЧНІ
ПРОЦЕСИ
Й
УСТАТКУВАННЯ
КПД
.
Такая
информация
важна
на
стадии
проектирования
диффузора
при
формировании
его
облика
.
Следует
также
отметить
,
что
изолинии
КПД
,
представленные
на
рис
. 2
б
,
могут
быть
получены
с
помощью
рис
. 2
а
,
если
иметь
ввиду
связи
параметров
Ср
,
η
,
A
2
/
A
1
:
(
)
2
1
2
1
1
A
A
Cp
−
=
η
,
где
отношение
площадей
(
A
2
/
A
1
),
записанное
в
знаменателе
правой
части
формулы
,
представляет
собой
ось
ординат
на
графике
рис
. 2
а
.
А
поэтому
пересечение
линий
Ср
= const
и
η
= const
на
рис
. 3
происходит
по
горизонталям
,
т
.
е
.
при
A
2
/
A
1
= const.
Таким
образом
,
изложен
графо
-
аналитический
метод
построения
плоских
диффузоров
на
основе
поляр
.
Список
литературы
:
1
.
Greitzer, E.M.
Coupled compressor diffuser flow in stability [Text] / E.M. Greitzer //
Journal of aircraft. – 1977. – Vol. 14,
№
3. –
Р
. 233-238.
2.
Герасименко
,
В
.
П
.
Параметрический
анализ
характеристик
кольцевого
диффузора
[
Текст
] /
В
.
П
.
Герасименко
,
Е
.
В
.
Осипов
//
Авиационно
-
космическая
техника
и
технология
.
Научно
-
технический
журнал
. –
Х
.:
ХАИ
. – 2008. –
№
6(53). –
С
. 84-89.
3.
Юдин
,
А
.
Ю
.
Исследование
осесимметричных
диффузоров
выхлопных
патрубков
турбомашин
со
специальным
вдувом
потока
[
Текст
] /
А
.
Ю
.
Юдин
//
Авиационно
-
космическая
техника
и
технология
.
Научно
-
технический
журнал
. –
Х
.:
ХАИ
. – 2011. –
№
3(80). –
С
. 80-84.
4.
Русанов
,
А
.
В
.
Аэродинамическое
усовершенствование
проточной
части
турбины
ГТД
на
основе
расчетов
трехмерного
вязкого
течения
.
Часть
2.
Переходной
диффузор
и
ступень
силовой
турбины
[
Текст
] /
А
.
В
.
Русанов
,
С
.
В
.
Ершов
,
Б
.
В
.
Исаков
[
и
др
.] //
Авиационно
-
космическая
техника
и
технология
.
Научно
-
технический
журнал
. –
Х
.:
ХАИ
. – 2004. –
№
8(16). –
С
. 46-50.
5.
Биндер
.
Разработка
и
применение
метода
расчета
рабочей
характеристики
прямолинейных
прямоугольных
диффузоров
[
Текст
] /
Биндер
,
Аль
-
Модафар
//
Тр
.
америк
.
общ
.
инж
.-
мех
.
Сер
.
Энергетические
машины
и
установки
. – 1983. –
№
1. –
С
. 84-88.
6.
Строн
.
Метод
расчета
плоских
и
осесимметричных
диффузоров
,
основанный
на
определении
запаса
по
отрыву
[
Текст
] /
Строн
,
Клайн
//
Тр
.
америк
.
общ
.
инж
.-
мех
.
Сер
.
Теоретические
основы
инженерных
расчетов
. – 1983. –
№
1. –
С
. 115-121.
7
.
Гоуз
.
Расчет
максимального
восстановления
давления
в
плоских
диффузорах
[
Текст
] /
Гоуз
,
Клайн
//
Тр
.
америк
.
общ
.
инж
.-
мех
.
Сер
.
Теоретические
основы
инженерных
расчетов
. – 1978. –
№
4. –
С
. 130-138.
8
.
Бардина
.
Метод
расчета
течения
в
плоских
диффузорах
[
Текст
] /
Бардина
,
Лирно
,
Клайн
,
Ферзигер
,
Джонстон
//
Тр
.
америк
.
общ
.
инж
.-
мех
.
Сер
.
Теоретические
основы
инженерных
расчетов
. – 1981. –
№
2. –
С
. 260-267.
9
.
Рено
.
Характеристики
и
расчет
плоских
диффузоров
с
прямолинейной
осью
[
Текст
] /
Рено
,
Джонстон
,
Клайн
//
Тр
.
америк
.
общ
.
инж
.-
мех
.
Сер
.
Теоретические
основы
инженерных
расчетов
. – 1967. –
№
1. –
С
. 160-172.
10.
Фокс
.
Режимы
течения
в
криволинейных
дозвуковых
диффузорах
[
Текст
] /
Фокс
,
Клайн
//
Техническая
механика
. – 1962. –
№
3. –
С
. 3-11.
11.
Энджаи
.
Неустойчивый
отрыв
потока
и
максимальное
восстановление
давления
в
двумерных
диффузорах
с
прямолинейными
стенками
[
Текст
] /
Энджаи
,
Джонстон
//
Тр
.
америк
.
общ
.
инж
.-
мех
.
Сер
.
Теоретические
основы
инженерных
расчетов
. – 1980. –
№
3. –
С
. 97-104.
12.
Лохманн
.
Закрученное
течение
в
кольцевых
диффузорах
с
коническими
стенками
[
Текст
] /
Лохманн
,
Марковски
,
Брукман
//
Тр
.
америк
.
общ
.
инж
.-
мех
.
Сер
.
Теоретические
основы
инженерных
расчетов
. – 1979. –
№
2. –
С
. 143-149.
13
.
Рено
.
Метод
определения
характеристик
плоских
безотрывных
диффузоров
[
Текст
] /
Рено
,
Джонстон
//
Тр
.
америк
.
общ
.
инж
.-
мех
.
Сер
.
Теоретические
основы
инженерных
расчетов
. – 1967. –
№
3. –
С
. 216-230.
14.
Zika, V.J.
Correlation and prediction of rotating stall inception by divergence method [Text] /
V.J. Zika // Trans. ASME. Journal of Fluid Engineering. – 1985. – Vol. 107, N 2. – P. 191-196.
15.
Титенский
,
В
.
И
.
Обобщение
опытных
данных
о
границе
помпажа
ступени
осевого
компрессора
[
Текст
] /
В
.
И
.
Титенский
//
Труды
ЦКТИ
. – 1970. –
Вып
. 102. –
С
. 76-85.
©
Герасименко
В
.
П
.,
Ткачук
А
.
С
.,
Яцышин
А
.
А
., 2012
Поступила
в
редколлегию
15.02.12
8’2012
142
ЕНЕРГЕТИЧНІ
ТА
ТЕПЛОТЕХНІЧНІ
ПРОЦЕСИ
Й
УСТАТКУВАННЯ
УДК
519.6
В
.
Н
.
ФЕНЧЕНКО
,
канд
.
физ
.-
мат
.
наук
;
с
.
н
.
с
.
Физико
-
технического
института
низких
температур
им
.
Б
.
И
.
Веркина
НАН
Украины
,
Харьков
;
О
.
В
.
КРАВЧЕНКО
,
канд
.
техн
.
наук
;
с
.
н
.
с
.
Института
проблем
машиностроения
им
.
А
.
Н
.
Подгорного
НАН
Украины
,
Харьков
;
В
.
И
.
МОМОТ
,
ведущий
инженер
Института
проблем
машиностроения
им
.
А
.
Н
.
Подгорного
НАН
Украины
,
Харьков
МОДЕЛИРОВАНИЕ
НЕСТАЦИОНАРНЫХ
ТЕЧЕНИЙ
ДИСПЕРСНЫХ
СИСТЕМ
С
ВЯЗКОЙ
ДИСПЕРСИОННОЙ
СРЕДОЙ
И
ТВЕРДОЙ
,
СИЛЬНО
НЕОДНОРОДНОЙ
ДИСПЕРСНОЙ
ФАЗОЙ
,
НЕСУЩЕЙ
ЭЛЕКТРИЧЕСКИЙ
ЗАРЯД
Предложен
метод
численного
решения
системы
уравнений
Навье
-
Стокса
-
Пуассона
-
Фоккера
-
Планка
,
описывающей
нестационарные
течения
дисперсной
системы
с
вязкой
дисперсионной
средой
и
твердой
сильно
неоднородной
дисперсной
фазой
,
несущей
электрический
заряд
под
действием
гравитационного
и
электростатического
полей
.
Запропоновано
метод
чисельного
розв
’
язку
системи
рівнянь
Навьє
-
Стокса
-
Пуасона
-
Фоккера
-
Планка
,
що
описує
нестаціонарні
течії
дисперсної
системи
з
в
’
язким
дисперсіонним
середовищем
і
твердою
дуже
неоднорідною
дисперсною
фазою
,
яка
несе
електричний
заряд
під
дією
гравітаційного
і
електростатичного
полів
.
The method for the numerical solution of the Navier-Stokes-Poisson-Fokker-Planck equations describing the
unsteady flow of a dispersed system with a viscous dispersion medium and a solid with strongly inhomogeneous
dispersed phase, which carries an electrical charge under the influence of gravitational and electrostatic fields is
proposed.
Введение
.
Во
многих
технологических
процессах
,
в
частности
,
при
производстве
и
классификации
порошковых
материалов
самого
различного
назначения
(
машиностроение
,
фармация
,
медицина
,
химия
наноматериалов
и
т
.
п
.),
при
производстве
композиционных
топлив
,
лакокрасочных
покрытий
,
наполненных
полимеров
,
смазочных
материалов
с
твердыми
присадками
,
все
большее
значение
приобретает
учет
особенностей
течения
дисперсных
систем
с
вязкой
дисперсионной
средой
и
твердой
сильно
неоднородной
дисперсной
фазой
,
несущей
электрический
заряд
[1, 2].
Когда
твердые
частицы
имеют
близкие
размеры
,
их
движение
может
быть
описано
в
рамках
так
называемой
«
двухфазной
модели
».
Однако
,
эта
модель
не
применима
для
сильно
неоднородных
дисперсных
систем
,
образованных
частицами
,
имеющими
значительный
разброс
по
размерам
.
Так
как
в
этом
случае
скорости
движения
разных
по
размеру
частиц
могут
сильно
различаться
,
то
для
описания
их
движения
необходимо
использовать
функцию
распределения
,
характеризующую
среднее
количество
частиц
с
определенным
разбросом
по
размерам
и
скоростям
в
элементе
пространства
.
Таким
образом
,
в
отличие
от
классической
системы
уравнений
Навье
-
Стокса
,
система
уравнений
,
описывающая
нестационарное
течение
вязкой
сильно
неоднородной
дисперсной
системы
,
содержит
дополнительный
интегральный
член
в
уравнении
движения
,
учитывающий
влияние
частиц
на
движение
несущей
дисперсионной
среды
,
а
для
расчета
функции
распределения
частиц
используется
уравнение
Фоккера
-
Планка
.
Кроме
того
,
для
электрически
заряженных
частиц
система
8’2012
143
ЕНЕРГЕТИЧНІ
ТА
ТЕПЛОТЕХНІЧНІ
ПРОЦЕСИ
Й
УСТАТКУВАННЯ
уравнений
должна
быть
дополнена
еще
и
уравнением
Пуассона
для
потенциала
поля
[3–5].
В
[6]
предложен
метод
численного
решения
начально
-
краевой
задачи
,
описывающей
нестационарные
течения
электрически
нейтральной
дисперсной
системы
,
основанный
на
схеме
расщепления
по
физическим
факторам
для
уравнения
движения
жидкой
дисперсионной
среды
и
использовании
метода
статистического
моделирования
при
решении
уравнения
Фоккера
-
Планка
для
функции
распределения
.
В
данной
работе
этот
метод
распространен
на
случай
,
когда
частицы
дисперсной
фазы
несут
электрический
заряд
и
,
следовательно
,
появляются
дополнительные
Кулоновские
силы
взаимодействия
частиц
между
собой
.
Вопросы
глобальной
разрешимости
подобных
начально
-
краевых
задач
рассматривались
,
в
частности
,
в
[5, 7, 8].
1
Уравнения
,
граничные
и
начальные
условия
.
Исходная
система
уравнений
,
описывающих
нестационарные
движения
дисперсной
системы
с
вязкой
несжимаемой
дисперсионной
средой
и
твердой
дисперсной
фазой
(
мелкими
твердыми
частицами
)
в
области
Ω
∈
x
,
имеет
вид
[3]
(
)
( )
(
) (
)
(
)
(
)
( )
[
]
,
4
3
,
2
9
,
,
;
,
,
,
;
0
div
;
,
,
,
,
6
,
2
2
f
D
f
g
r
w
t
x
u
r
f
w
t
f
dwdr
t
r
w
x
rf
q
u
g
p
dwdr
t
r
w
x
f
w
t
x
u
r
u
u
u
t
u
w
x
p
w
x
r w
r w
f
x
x
∆
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
+
ϕ
∇
πρ
−
−
ν
∇
+
∇
+
∂
∂
−
=
ϕ
∆
=
=
ρ
∇
+
−
πν
+
∆
ν
−
∇
+
∂
∂
∫∫
∫∫
где
ν
–
кинематическая
вязкость
дисперсионной
среды
;
ρ
f
–
ее
плотность
;
(
t
x
u
u
,
=
)
–
поле
скоростей
;
(
t
x
p
p
,
=
)
–
поле
давления
;
ρ
p
–
плотность
частиц
твердой
дисперсной
фазы
;
q
–
объемная
плотность
заряда
частиц
;
g
–
внешняя
массовая
сила
,
действующая
на
единицу
объема
;
(
t
x
,
ϕ
=
ϕ
)
–
потенциал
электрического
поля
частиц
;
D
–
коэффициент
диффузии
,
а
(
)
t
r
w
x
f
f
,
,
,
=
–
функция
распределения
частиц
дисперсной
фазы
в
пространстве
по
скоростям
и
радиусам
.
На
участке
,
где
дисперсная
система
поступает
в
расчетную
область
,
задаем
поле
скоростей
среды
,
объемную
плотность
частиц
в
потоке
,
их
заряд
и
функцию
распределения
по
радиусам
,
полагая
,
что
скорости
частиц
на
входе
соответствуют
скорости
потока
,
а
там
,
где
она
покидает
расчетную
область
,
ставим
условие
свободного
вытекания
,
на
твердой
стенке
–
условия
не
протекания
и
прилипания
,
а
на
свободной
границе
–
условие
не
протекания
и
скольжения
.
Для
функции
распределения
ставим
условия
поглощения
частиц
границей
,
зеркального
или
диффузного
отражения
.
Для
потенциала
электрического
поля
задаем
условия
убывания
на
бесконечности
и
условие
Дирихле
на
проводящей
части
границы
расчетной
области
.
В
начальный
момент
задаем
распределение
скорости
,
удовлетворяющее
уравнению
неразрывности
и
граничным
условиям
,
а
также
начальное
значение
функции
распределения
,
удовлетворяющее
граничным
условиям
.
8’2012
144