ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 26.10.2023
Просмотров: 353
Скачиваний: 5
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Описанию некоторых предложенных Кумбсом типологий шкал будет посвящен следующий раздел.
Перейдем к рассмотрению метода одномерного развертывания, начав с постановки задачи и анализа соответствующей модели восприятия. По существу речь пойдет о том, при каких минимальных предположениях и как может быть построена оценочная шкала, исходной информацией для которой служат осуществленные респондентами ранжировки шкалируемых объектов.
9.2. Основная цель метода
(Итак, в нашем распоряжении имеются осуществленные респондентами ранжировки изучаемых объектов. Задача состоит в приписывании объектам чисел таким образом, чтобы эти числа отражали суммарное (усредненное) мнение всех респондентов о рассматриваемых объектах. Ясно, что это — одна из самых распространенных задач эмпирической социологии.
В первом разделе мы рассматривали традиционные способы /решения подобных задач. Надеемся, читатель убедился в том, что корректность этих способов может быть поставлена под сомнение. Как же быть?
Прежде всего вспомним, в чем именно мы усматривали "корень зла". При этом рассмотрим лишь часть сформулированных выше проблем. А именно: предположим, что мы "верим" ранжировкам и обратимся к рассмотренному в п. 1.2 примеру: предположим, что оценочная шкала получается за счет усреднения рангов, приписанных респондентами тому или иному объекту.
Неадекватность этого способа мы усматривали в том, что, усредняя баллы, мы тем самым обращались с ними как с числами, неявно учитывая такие соотношения между ними, как, например, 5 — 4 = 3-2. И по сути дела, у нас не было никаких соображений, делающих такой способ обращения с числами адекватным. Респондент нам говорил о том, что такой-то объект он ставит на третье место, но при этом никак не намекал, что имеет в виду приписывание этому объекту числа 3.
Кумбс поставил перед собой вопрос: можно ли, не вкладывая в ответы респондента того, чего он не говорил, не навязывая ему чисел, все же как-то построить требующуюся оценочную шкалу?
Итак, можно ли на базе осуществленных респондентами ранжировок изучаемых объектов, не делая никаких искусственных предположений, построить оценочную шкалу? Если вообще без всяких предположений нельзя обойтись, то каким должен быть их наиболее "безвредный" минимум? Другими словами, какова должна быть модель восприятия, чтобы, с одной стороны, она дала нам возможность построить требующуюся шкалу, а с другой, — была бы приемлема, не опиралась на слишком далекие от действительности предположения? Кумбс дал ответ на этот вопрос. Этот ответ состоял в предложении особого способа шкалирования: метода одномерного развертывания.
Таким образом, основная цель указанного метода — построение оценочной шкалы на базе ранжировок изучаемых объектов и с использованием сравнительно приемлемой модели восприятия (во всяком случае, не опирающейся на подмену рангов числами).
Как и выше, предположим, что исследователя интересует,-каким для рассматриваемой совокупности респондентов является, скажем, рейтинг каких-то политических лидеров, либо популярность каких-то телепередач, либо престижность ряда профессий. И для получения исходных данных социолог просит каж<-дого респондента проранжировать соответственно политических лидеров, телепередачи, профессии. О том, какое основание классификации предлагается выбрать, мы пока не говорим. Этот выбор в значительной мере предопределяет модель восприятия, к обсуждению которой мы переходим.
9.3. Модель восприятия
Интересующая нас модель восприятия респондентами предлагаемых им для ранжирования объектов состоит в том, что мы считаем адекватными реальности следующие предположения.
Прежде всего, как и выше, считаем, что существует некоторая прямая (числовая ось), на которой расположены рассматриваемые объекты. В соответствии со смыслом оценочной шкалы такое расположение отвечает некой усредненной "симпатии" респондентов к этим объектам. В частности, если один объект лежит на прямой левее другого, то первый в среднем более "симпатичен" респондентам. Наша основная задача как раз в том и состоит, чтобы найти это расположение.
Ясно, что упомянутую прямую можно считать отвечающей латентной переменной, измерение которой является нашей целью.
Представляется естественным прежде всего поставить вопрос о том, как наши ранжировки соотносятся с описанной прямой. Кумбс предложил две трактовки (интерпретации) ранжировок. Каждая из них отвечает определенной модели восприятия. Одну из этих моделей Кумбс положил в основу метода одномерного развертывания.
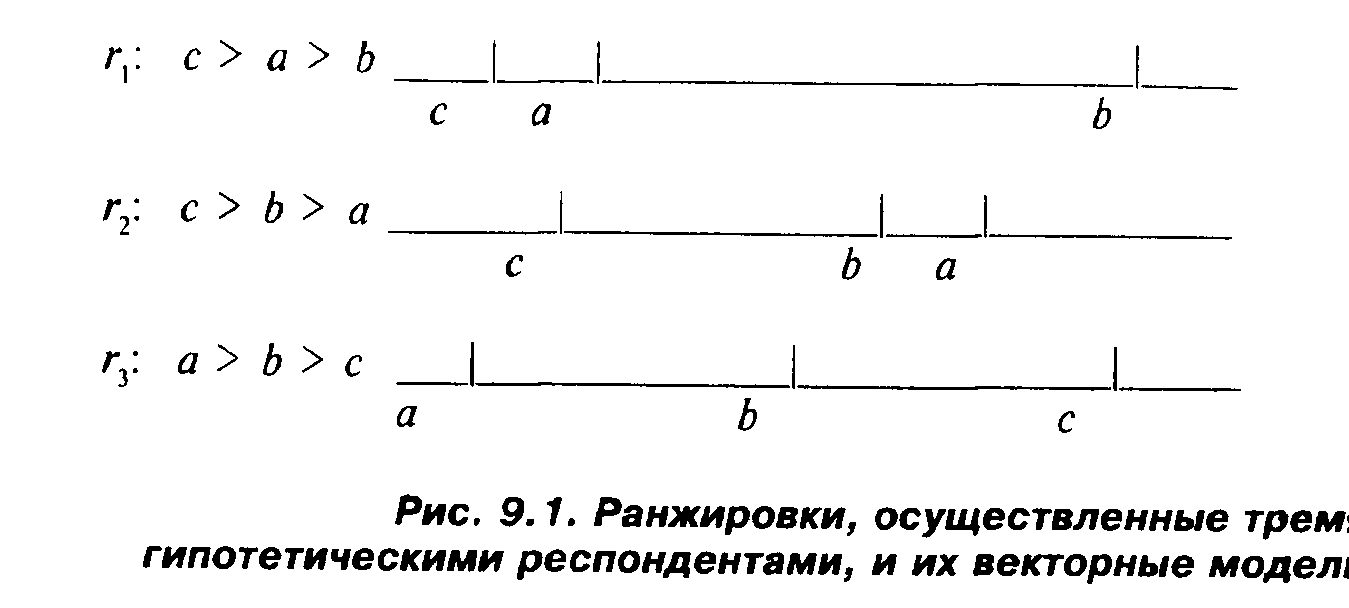
Первая — векторная модель — предполагает, что респонденты осознают наличие упомянутой латентной переменной и, ранжируя объекты, делают это в зависимости от своих субъективных представлений о том, в какой мере соответствующее качество в каждом объекте содержится. Скажем, если рассматриваются три объекта a,bи с и какие-то три респондента г,, гг
и г3 дали нам ранжировки, приведенные на рис. 9.1 слева, то им будут отвечать модели (отражающие субъективные представления соответствующих респондентов о расположении объектов на оси), изображенные на том же рисунке справа. Подчеркнем, что эти модели,конечно, не являются однозначными. Скажем, для объекта г, точки, отвечающие рассматриваемым объектам, могут быть расположены на прямой как угодно при единственном условии: точка, отвечающая объекту с, должна быть левее точки, отвечающей а,а последняя, в свою очередь, должна быть левее точки, отвечающей объекту Ь.
Приведем пример. Пусть а, Ь, с — политические лидеры, и мы предлагаем экспертам /·,, гг, г}оценить этих лидеров с точки зрения их честности. Каждый из экспертов в процессе ранжировки претендентов думал именно о честности и, ранжируя их, фактически высказал свое мнение на этот счет. Мнения разошлись. Первый эксперт полагал, что самым честным является лидер с, на втором месте — Ь, самый нечестный — а.Второй был согласен с первым в отношении определения самого честного претендента, но по поводу двух остальных думал по-другому — считал, что а честнее Ь, и т.д. И это нашло отражение в соответствующих геометрических картинках.
Находить "истинное" расположение объектов на прямой в таком случае мы можем только расценивая рассматриваемые ранжировки как случайные реализации некоего "усредненного" расположения объектов. Такая интерпретация приводит нас к рассуждениям, подобным тем, которые были использованы при обсуждении установочной шкалы Терстоуна в 5.2.2. И перед нами встают те же проблемы. Обычные способы усреднения заставят нас пользоваться многими непроверяемыми предположениями, чего Кумбс хотел избежать. Именно поэтому при решении рассматриваемой задачи он взял на "вооружение" не векторную модель, а другую, им же предложенную.
Вторая модель, отражающая несколько иную интерпретацию ранжировок, — модель идеальной точки — состоит в следующем. Обращаясь к экспертам с просьбой проранжировать объекты, исследователь не говорит о том, по какому конкретному качеству ранжировки должны осуществляться. Вопрос ставится в более общем виде — скажем, предлагается проранжировать телепередачи в соответствии с тем, насколько каждая из них нравится эксперту
Рис. 9.2. Произвольноерасположениешкалируемыхобъектовнаоси (первыйшагпримененияметодаодномерногоразвертывания)
Теперь сформулируем простейшее геометрическое соображение: если на прямой даны две "зарубки" α и Ь, то геометрическим местом точек, более близких к правой, чем к левой, будет
(для политических лидеров — по тому, насколько они, по мнению эксперта, подходят на должность президента страны; для профессий — по их престижности). Предполагается, что:
у каждого эксперта сформировано представление об "идеальном" для него объекте (скажем, о безоговорочно ему нравящейся телепередаче, идеальном президенте страны, самой престижной профессии) и у этого "идеального" объекта имеется какое-то "объективное" место на упомянутой прямой;
в процессе ранжировки эксперт отдает большее предпочтение тому объекту, "объективное" место которого на прямой находится ближе к идеальной точке этого эксперта.
Базируясь на этих предположениях и опираясь на данные респондентами ранжировки, мы должны найти "объективное" (усредненное) расположение объектов на прямой (хотя бы с какой-нибудь точностью, т.е., проще говоря, хотя бы что-то узнать об этом расположении). Кроме того, при рассмотренной постановке вопроса возникает еще одна задача — интерпретация самой прямой. Задача довольно типична для социологии и родственна задаче интерпретации латентных факторов в ФА и ЛСА.
Итак, пусть какие-то три респондента имеют ранжировки, изображенные на рис. 9.1. Опираясь на нашу модель и не делая никаких других модельных предположений, попытаемся расположить объекты на оси. Вернее, покажем, как это делал Кумбс.
9.4. Техника одномерного развертывания
Сначала разместим объекты на оси произвольным образом (рис. 9.2) и попытаемся выяснить, как в таком случае на той же оси могут расположиться идеальные точки наших трех респондентов.
полупрямая, идущая вправо от середины отрезка между нашими "зарубками".
-μ = = =
Рис. 9.3.
Нахождениегеометрическогоместаточек, лежащихнаосиближекобъектуЬ, чемкобъектуа
На рисунке двойным пунктиром обозначена та часть прямой, все точки которой расположены ближе к Ь, чем к а.
На рис. 9.4 буквами а, Ь, с обозначены шкалируемые объекты; сочетаниями ас, ab, be— середины отрезков между соответствующими объектами. Каждой середине отвечает вертикальная черта, от которой отходят горизонтальные стрелки, указывающие, какую из двух отвечающих этой черте полупрямых заполняют идеальные точки того респондента, ранжировка которого указана на том же уровне справа.
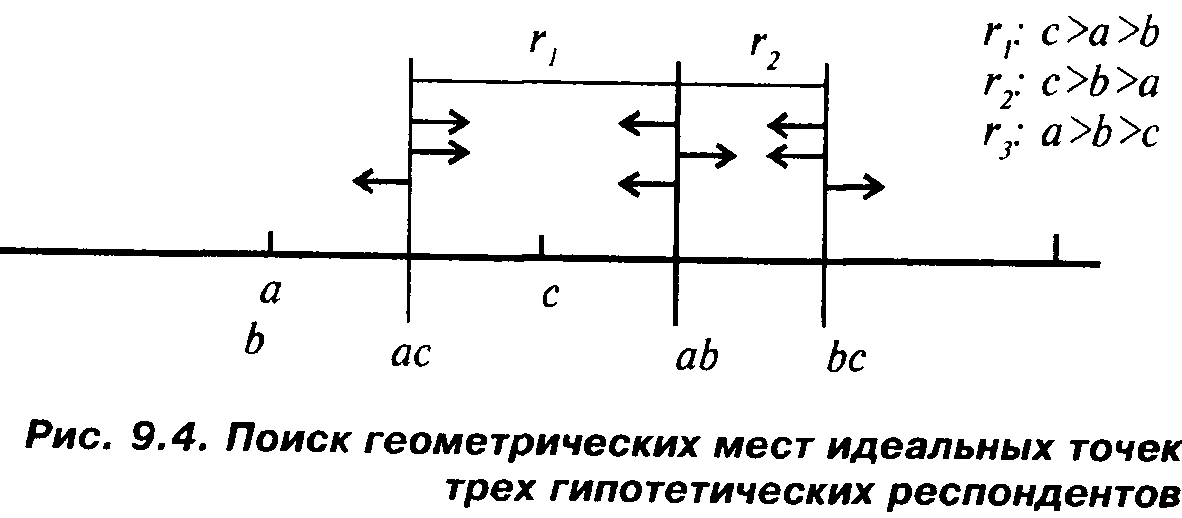
Например, первому респонденту, давшему ранжировку с>а>Ь, отвечает верхний уровень рисунка. Справа фигурирует указанная ранжировка. Опираясь на нее, рассмотрим, как этот респондент попарно соотносил друг с другом все рассматриваемые объекты. Соотношение с>а говорит о том, что идеальная точка первого респондента должна находиться на полупрямой, идущей вправо от вертикали ас. Соотношение с>Ь — о том, что та же точка должна лежать на полупрямой, идущей влево от вертикали be. Соотношение же а>Ь— о том, что той же точке будет отвечать полупрямая, идущая влево от вертикали ab. Поскольку сказанное справедливо относительно идеальной точки одного и того же респондента, то можно сказать, что эта точка лежит на пересечении названных полупрямых. Таким пересечением является отрезок от середины ас до середины аЬ. Более точно определить место идеальной точки первого респондента мы не можем — имеющаяся в нашем распоряжении информация не дает возможности этого сделать.
Рассуждая аналогичным образом относительно второго респондента (которому отвечает второй сверху уровень рис. 9.4), мы придем к выводу, что отвечающая ему идеальная точка лежит между серединами