ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 26.10.2023
Просмотров: 342
Скачиваний: 5
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
А в ячейку 2, а суждение Б — в ячейку 3, а потом, рассматривая карточку с суждением М, вдруг решил, что оно занимает промежуточное положение между А и Б. Тогда он может положить карточку с суждением Μ в ячейку 3 , а суждение Б — в ячейку 4. И таких перестановок может быть много. Полагаем очевидным тот факт, что, проставляя ранги рядом с написанными на листе бумаги суждениями, эксперт быстро запутается, да и может просто "отключиться" из-за неудобства способа фиксации своих соображений, даст исследователю некий полуфабрикат своих размышлений.
Последнее наше замечание касается количества используемых ячеек. Именно 11 ячеек было предложено самим Терстоуном, который определил это количество, опираясь на свой опыт психофизика. В принципе можно говорить и о другом числе ячеек (что предлагают, например, авторы [Рабочая книга..., 1983]). Но при этом надо учитывать ряд обстоятельств, связанных с тем, какого типа шкалу мы хотим получить. Соответствующие аспекты требуют довольно тонких рассмотрений. Осуществим их в п. 5.2.
Р
езультаты экспертного опроса лучше всего фиксировать с помощью построения таблицы следующего вида (табл. 5.1).
Ясно, что первое и второе суждения мы должны отбросить, поскольку мнения экспертов об этих суждениях резко расходятся: относительно первого суждения половина экспертов считает, что оно отвечает максимально положительному отношению к предмету установки, а половина — максимально отрицательному; относительно второго суждения мнения экспертов распределились приблизительно равномерно по всему диапазону возможных изменений значений измеряемой установки.
Третье суждение заведомо должно быть оставлено, причем его цена должна быть равна 1: все респонденты единодушно считают, что это суждение отвечает максимально положительному отношению к предмету установки.
Относительно четвертого суждения мы не можем судить столь однозначно. Но все же, наверное, мы его оставим, поскольку разброс мнений экспертов не очень велик. И цена суждения, вероятно, должна находиться между 2 и 3, ближе к 3. Но где ее точное местоположение?
Положение пятого суждения еще менее очевидно. И таких неочевидных ситуаций на практике, конечно, бывает очень много. Встает вопрос, как оценить степень разброса мнений экспертов и найти "цену" суждения в произвольном случае.
Чтобы ответить на поставленные вопросы, дадим себе отчет в том, что мы имеем дело с порядковой шкалой (каждый эксперт, помещая суждение в ту или иную ячейку, фактически приписывает ему шкальное значение, отвечающее именно порядковой шкале), и вспомним, какие средние и какие меры разброса осмыслены для этой шкалы [Ядов, 1995] (строгое определение понятия адекватности математического метода относительно типа используемых шкал будет дано в главе 14).
В качестве средних для порядковой шкалы можно использовать квартили точки, которые делят вариационный ряд значений рассматриваемого признака на четыре равнонаполненные части (напомним, что вариационным рядом, отвечающим какому-либо набору чисел, называется последовательность этих чисел, расположенных в порядке их возрастания). Квартили обычно обозначаются буквами QrQ2, Q3. Второй квартиль называется также медианой и обозначается как Me. Ql— такое значение признака, что одна четвертая часть всех объектов имеет значения, меньшие него, а три четверти — значения, большие него; Q2 = Me — такое значение, что половина всех объектов имеет значения, меньшие него, а половина большие; Q3— такое значение, что значения трех
четвертей объектов меньше него, а одной четверти — больше. Схематически эта ситуация изображена на рис. 5.1.
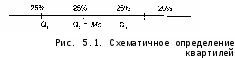
В качестве меры разброса для порядковой шкалы используется квартальный размах, равный (Q3- (?,). Определение квартилей можно найти, например, в [Паниотто, Максименко, 1982; Рабочая книга..., 1983; Ядов, 1995]. Значения их обычно находят с помощью расчета так называемой кумуляты — графика накопленных частот. Ниже будут приведены примеры.
Терстоун предложил в качестве цены суждения использовать отвечающую ему медиану, о мере разброса мнений экспертов судить по соответствующему квартильному размаху и суждения с большим квартальным размахом отбрасывать.
О том, какой квартальный размах имеет смысл считать большим, исследователь может судить, опираясь на определенный практический опыт. Только имея перед глазами весь набор "раз-махов", вычисленных для конкретного случая, можно сказать, каким должно быть наше "пороговое значение". Более того, на практике вполне возможна такая ситуация, когда мы можем прийти к выводу о целесообразности отбросить суждение с меньшим разбросом приписанных ему значений и оставить суждение с большим разбросом. Это возможно в случае, если первое суждение имеет цену, близкую к ценам каких-то
других суждений с малым разбросом, а второе — цену, рядом с которой на нашей оси нет цен других суждений. Второе суждение в таком случае может быть значимым для нас, поскольку оно представляет "пустую" (не заполненную другими суждениями) часть континуума.
Другими словами, имеет смысл "разгрузить" чересчур заполненные места континуума путем уменьшения для соответствующих суждений величины порога. И, напротив, суждения, встречающиеся в "пустынных" местах нашей гипотетической оси, должны стать для нас особо ценными, и для них порог можно увеличить (правда, на следующих этапах работы о соответствующей ненадежности суждений иногда имеет смысл вспомнить).
Отметим, что приведенные рассуждения имеют смысл лишь в том случае, когда мы считаем исходные 11 градаций как бы равно отстоящими друг от друга (иначе теряют смысл рассуждения о том, что суждения могут неравномерно заполнять ось: ведь для порядковой шкалы определен только порядок расположения шкальных значений на психологическом континууме). О том, почему такое предположение можно считать оправданным, пойдет речь в п. 5.2.3.
5.1.3. Опросреспондентов
иприписываниеимшкальныхзначений
Если первые два этапа были посвящены построению вспомогательной оценочной шкалы — шкалы для суждений (результатом реализации этих этапов было расположение суждений на числовой оси), то оставшиеся этапы — построению главной интересующей нас шкалы — установочной, дающей возможность каждому респонденту приписать число, отвечающее его установке.
Итак, составляем список оставленных нами суждений и включаем его в анкету, предназначенную для опроса основной массы респондентов. Сопровождаем список преамбулой, в которой просим отвечающего отметить номер того суждения, с которым он согласен. Суждения даются в случайном порядке, их веса остаются респондентам неизвестными. Проводим анкетирование.
Последний этап обычно осуществляется с помощью ЭВМ. Для каждого респондента находим среднее значение (медиану) цен тех суждений, с которыми этот респондент согласен. Это среднее и будет искомым шкальным значением респондента, результатом измерения его установки. Оно включается в анкету как значение новой переменной (искомой установки). Далее мы можем такого рода значения использовать так же, как значения любого другого признака: находить и анализировать его распределение, изучать его связи с другими признаками и т.д.
5.2. Модельные представления
Отметим некоторые моменты, характеризующие ту модель "поведения" респондента, которая фактически используется при построении шкалы Терстоуна, но обычно не оговаривающиеся в литературе. Важность четкой формулировки соответствующих предположений объясняется, в частности, тем, что многие из них используются и в других методах шкалирования. Часть интересующих нас методических аспектов уже была затронута при описании отдельных этапов шкалирования. Ниже мы фактически продолжим соответствующее обсуждение.
Итак, обращаем внимание читателя на следующие свойства модели, используемой при построении установочной шкалы Терстоуна.
5.2.1. Сочетаниемягкойижесткойстратегий
При реализации рассматриваемого подхода происходит то самое сочетание мягкой и жесткой стратегий сбора данных, о которых мы говорили в пп. 3.2 и 4.1.
С одной стороны, "снимая" с респондентов информацию, т.е. реализуя третий этап шкалирования, мы используем сравнительно простую жесткую процедуру: просим каждого респондента согласиться либо не согласиться с каждым из предлагаемых суждений. С помощью этой процедуры можно в короткие сроки опросить огромное количество респондентов. Результаты опроса вряд ли могут вызвать сильное недоверие исследователя (правда, вероятно, в некоторых ситуациях было бы целесообразно учесть, что степень согласия респондента с тем или иным суждением может быть разной и в этой связи было бы интересно изучить возможности построения "гибрида" шкалы Терстоуна с описываемой нами ниже шкалой Лайкерта).
С другой стороны, как нетрудно понять, в подготовку этого простого (для респондента!) способа опроса вложено много "мягкости": это и наши соображения по поводу понимания установки, и идеи, лежащие в основе формирования суждений, и согласование мнения исследователя с мнением потенциальных респондентов. Именно сочетание жесткости и мягкости дает нам желаемый эффект — адекватное отражение значений латентной переменной в числовую систему.
5.2.2. Распределения, отвечающиеэкспертам
исуждениям. Ихсоотношение
1) Рассматриваемый подход к шкалированию иллюстрирует положение о том, что не существует принципиального различия между оценочными и установочными шкалами: процесс построения установочной шкалы, т.е. приписывания чисел респондентам, здесь явно включает в себя предварительное построение оценочной шкалы, т.е. приписывание чисел суждениям.
Надеемся, что читатель воспринял как естественный шаг размещение и респондентов, и оцениваемых ими объектов (суждений) на одной числовой оси. Однако наш опыт говорит о том, что иногда осознание соответствующей возможности приходит с трудом. Подход же этот очень важен. Он используется, в частности, в некоторых ветвях многомерного шкалирования (в многомерном развертывании), давая возможность социологу получить оригинальные выводы [Интерпретация и анализ..., 1987, гл. 8; Клигер и др., 1978, гл. 4]. Поэтому остановимся более подробно на этом фрагменте нашей модели.
Вообще говоря, упомянутое размещение может выглядеть странно. Не придет же нам в голову помещать на одну ось (точнее, считать адекватной соответствующую модель), скажем, людей, для которых измерен рост (диапазон от 150 до 200 см), и мешки с зерном, для которых измерен вес (тот же диапазон от 150 до 200, но не см, а кг). Казалось бы, респонденты и суждения — тоже разноплановые объекты. И размещение их на одной оси (т.е. рассмотрение их как точек одного и того же психологического континуума) оказывается логичным только потому, что на самом-то деле для нас, в нашей модели, они являют собой разные ипостаси одной природы: респонденты нас интересуют как выразители мнений о суждениях, суждения — как носители мнений, определенного к ним отношения респондентов. Мы как бы "забываем" о том, что каждый респондент — уникальная личность (скажем, романтически настроенный блондин с голубыми глазами) и что каждое суждение может быть охарактеризовано, скажем, количеством входящих в него глаголов совершенного вида или гласных букв, оценено с точки зрения его литературных достоинств и т.д.
Точки нашей прямой говорят нам, с одной стороны, об эмоциональном настрое респондентов по отношению к предмету установки, а с другой, — о том, насколько этот настрой отражается в рассматриваемых суждениях. А это представляется вполне естественным. Рассматриваемая ситуация изображена на рис.5.2, где на одной и той же прямой размещаются респонденты /*,, г2, rk(обозначаемые нами кружками) и суждения srs2, st (обозначаемые нами крестиками).
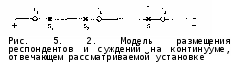
Слева на прямой — точки, отвечающие положительному эмоциональному настрою по отношению к предмету установки, справа — отрицательному настрою. Чем правее находится точка, тем более отрицательный настрой ей отвечает (отметим, что определение направления "возрастания" шкальных значений наших объектов весьма условно: увеличение их может происходить как справа налево, так и наоборот, надо только четко оговорить, какой вариант мы выбираем).
Последнее наше замечание касается количества используемых ячеек. Именно 11 ячеек было предложено самим Терстоуном, который определил это количество, опираясь на свой опыт психофизика. В принципе можно говорить и о другом числе ячеек (что предлагают, например, авторы [Рабочая книга..., 1983]). Но при этом надо учитывать ряд обстоятельств, связанных с тем, какого типа шкалу мы хотим получить. Соответствующие аспекты требуют довольно тонких рассмотрений. Осуществим их в п. 5.2.
Р

езультаты экспертного опроса лучше всего фиксировать с помощью построения таблицы следующего вида (табл. 5.1).
Ясно, что первое и второе суждения мы должны отбросить, поскольку мнения экспертов об этих суждениях резко расходятся: относительно первого суждения половина экспертов считает, что оно отвечает максимально положительному отношению к предмету установки, а половина — максимально отрицательному; относительно второго суждения мнения экспертов распределились приблизительно равномерно по всему диапазону возможных изменений значений измеряемой установки.
Третье суждение заведомо должно быть оставлено, причем его цена должна быть равна 1: все респонденты единодушно считают, что это суждение отвечает максимально положительному отношению к предмету установки.
Относительно четвертого суждения мы не можем судить столь однозначно. Но все же, наверное, мы его оставим, поскольку разброс мнений экспертов не очень велик. И цена суждения, вероятно, должна находиться между 2 и 3, ближе к 3. Но где ее точное местоположение?
Положение пятого суждения еще менее очевидно. И таких неочевидных ситуаций на практике, конечно, бывает очень много. Встает вопрос, как оценить степень разброса мнений экспертов и найти "цену" суждения в произвольном случае.
Чтобы ответить на поставленные вопросы, дадим себе отчет в том, что мы имеем дело с порядковой шкалой (каждый эксперт, помещая суждение в ту или иную ячейку, фактически приписывает ему шкальное значение, отвечающее именно порядковой шкале), и вспомним, какие средние и какие меры разброса осмыслены для этой шкалы [Ядов, 1995] (строгое определение понятия адекватности математического метода относительно типа используемых шкал будет дано в главе 14).
В качестве средних для порядковой шкалы можно использовать квартили точки, которые делят вариационный ряд значений рассматриваемого признака на четыре равнонаполненные части (напомним, что вариационным рядом, отвечающим какому-либо набору чисел, называется последовательность этих чисел, расположенных в порядке их возрастания). Квартили обычно обозначаются буквами QrQ2, Q3. Второй квартиль называется также медианой и обозначается как Me. Ql— такое значение признака, что одна четвертая часть всех объектов имеет значения, меньшие него, а три четверти — значения, большие него; Q2 = Me — такое значение, что половина всех объектов имеет значения, меньшие него, а половина большие; Q3— такое значение, что значения трех
четвертей объектов меньше него, а одной четверти — больше. Схематически эта ситуация изображена на рис. 5.1.
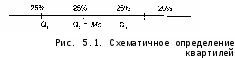
В качестве меры разброса для порядковой шкалы используется квартальный размах, равный (Q3- (?,). Определение квартилей можно найти, например, в [Паниотто, Максименко, 1982; Рабочая книга..., 1983; Ядов, 1995]. Значения их обычно находят с помощью расчета так называемой кумуляты — графика накопленных частот. Ниже будут приведены примеры.
Терстоун предложил в качестве цены суждения использовать отвечающую ему медиану, о мере разброса мнений экспертов судить по соответствующему квартильному размаху и суждения с большим квартальным размахом отбрасывать.
О том, какой квартальный размах имеет смысл считать большим, исследователь может судить, опираясь на определенный практический опыт. Только имея перед глазами весь набор "раз-махов", вычисленных для конкретного случая, можно сказать, каким должно быть наше "пороговое значение". Более того, на практике вполне возможна такая ситуация, когда мы можем прийти к выводу о целесообразности отбросить суждение с меньшим разбросом приписанных ему значений и оставить суждение с большим разбросом. Это возможно в случае, если первое суждение имеет цену, близкую к ценам каких-то
других суждений с малым разбросом, а второе — цену, рядом с которой на нашей оси нет цен других суждений. Второе суждение в таком случае может быть значимым для нас, поскольку оно представляет "пустую" (не заполненную другими суждениями) часть континуума.
Другими словами, имеет смысл "разгрузить" чересчур заполненные места континуума путем уменьшения для соответствующих суждений величины порога. И, напротив, суждения, встречающиеся в "пустынных" местах нашей гипотетической оси, должны стать для нас особо ценными, и для них порог можно увеличить (правда, на следующих этапах работы о соответствующей ненадежности суждений иногда имеет смысл вспомнить).
Отметим, что приведенные рассуждения имеют смысл лишь в том случае, когда мы считаем исходные 11 градаций как бы равно отстоящими друг от друга (иначе теряют смысл рассуждения о том, что суждения могут неравномерно заполнять ось: ведь для порядковой шкалы определен только порядок расположения шкальных значений на психологическом континууме). О том, почему такое предположение можно считать оправданным, пойдет речь в п. 5.2.3.
5.1.3. Опросреспондентов
иприписываниеимшкальныхзначений
Если первые два этапа были посвящены построению вспомогательной оценочной шкалы — шкалы для суждений (результатом реализации этих этапов было расположение суждений на числовой оси), то оставшиеся этапы — построению главной интересующей нас шкалы — установочной, дающей возможность каждому респонденту приписать число, отвечающее его установке.
Итак, составляем список оставленных нами суждений и включаем его в анкету, предназначенную для опроса основной массы респондентов. Сопровождаем список преамбулой, в которой просим отвечающего отметить номер того суждения, с которым он согласен. Суждения даются в случайном порядке, их веса остаются респондентам неизвестными. Проводим анкетирование.
Последний этап обычно осуществляется с помощью ЭВМ. Для каждого респондента находим среднее значение (медиану) цен тех суждений, с которыми этот респондент согласен. Это среднее и будет искомым шкальным значением респондента, результатом измерения его установки. Оно включается в анкету как значение новой переменной (искомой установки). Далее мы можем такого рода значения использовать так же, как значения любого другого признака: находить и анализировать его распределение, изучать его связи с другими признаками и т.д.
5.2. Модельные представления
Отметим некоторые моменты, характеризующие ту модель "поведения" респондента, которая фактически используется при построении шкалы Терстоуна, но обычно не оговаривающиеся в литературе. Важность четкой формулировки соответствующих предположений объясняется, в частности, тем, что многие из них используются и в других методах шкалирования. Часть интересующих нас методических аспектов уже была затронута при описании отдельных этапов шкалирования. Ниже мы фактически продолжим соответствующее обсуждение.
Итак, обращаем внимание читателя на следующие свойства модели, используемой при построении установочной шкалы Терстоуна.
5.2.1. Сочетаниемягкойижесткойстратегий
При реализации рассматриваемого подхода происходит то самое сочетание мягкой и жесткой стратегий сбора данных, о которых мы говорили в пп. 3.2 и 4.1.
С одной стороны, "снимая" с респондентов информацию, т.е. реализуя третий этап шкалирования, мы используем сравнительно простую жесткую процедуру: просим каждого респондента согласиться либо не согласиться с каждым из предлагаемых суждений. С помощью этой процедуры можно в короткие сроки опросить огромное количество респондентов. Результаты опроса вряд ли могут вызвать сильное недоверие исследователя (правда, вероятно, в некоторых ситуациях было бы целесообразно учесть, что степень согласия респондента с тем или иным суждением может быть разной и в этой связи было бы интересно изучить возможности построения "гибрида" шкалы Терстоуна с описываемой нами ниже шкалой Лайкерта).
С другой стороны, как нетрудно понять, в подготовку этого простого (для респондента!) способа опроса вложено много "мягкости": это и наши соображения по поводу понимания установки, и идеи, лежащие в основе формирования суждений, и согласование мнения исследователя с мнением потенциальных респондентов. Именно сочетание жесткости и мягкости дает нам желаемый эффект — адекватное отражение значений латентной переменной в числовую систему.
5.2.2. Распределения, отвечающиеэкспертам
исуждениям. Ихсоотношение
1) Рассматриваемый подход к шкалированию иллюстрирует положение о том, что не существует принципиального различия между оценочными и установочными шкалами: процесс построения установочной шкалы, т.е. приписывания чисел респондентам, здесь явно включает в себя предварительное построение оценочной шкалы, т.е. приписывание чисел суждениям.
Надеемся, что читатель воспринял как естественный шаг размещение и респондентов, и оцениваемых ими объектов (суждений) на одной числовой оси. Однако наш опыт говорит о том, что иногда осознание соответствующей возможности приходит с трудом. Подход же этот очень важен. Он используется, в частности, в некоторых ветвях многомерного шкалирования (в многомерном развертывании), давая возможность социологу получить оригинальные выводы [Интерпретация и анализ..., 1987, гл. 8; Клигер и др., 1978, гл. 4]. Поэтому остановимся более подробно на этом фрагменте нашей модели.
Вообще говоря, упомянутое размещение может выглядеть странно. Не придет же нам в голову помещать на одну ось (точнее, считать адекватной соответствующую модель), скажем, людей, для которых измерен рост (диапазон от 150 до 200 см), и мешки с зерном, для которых измерен вес (тот же диапазон от 150 до 200, но не см, а кг). Казалось бы, респонденты и суждения — тоже разноплановые объекты. И размещение их на одной оси (т.е. рассмотрение их как точек одного и того же психологического континуума) оказывается логичным только потому, что на самом-то деле для нас, в нашей модели, они являют собой разные ипостаси одной природы: респонденты нас интересуют как выразители мнений о суждениях, суждения — как носители мнений, определенного к ним отношения респондентов. Мы как бы "забываем" о том, что каждый респондент — уникальная личность (скажем, романтически настроенный блондин с голубыми глазами) и что каждое суждение может быть охарактеризовано, скажем, количеством входящих в него глаголов совершенного вида или гласных букв, оценено с точки зрения его литературных достоинств и т.д.
Точки нашей прямой говорят нам, с одной стороны, об эмоциональном настрое респондентов по отношению к предмету установки, а с другой, — о том, насколько этот настрой отражается в рассматриваемых суждениях. А это представляется вполне естественным. Рассматриваемая ситуация изображена на рис.5.2, где на одной и той же прямой размещаются респонденты /*,, г2, rk(обозначаемые нами кружками) и суждения srs2, st (обозначаемые нами крестиками).
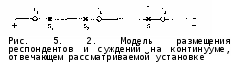
Слева на прямой — точки, отвечающие положительному эмоциональному настрою по отношению к предмету установки, справа — отрицательному настрою. Чем правее находится точка, тем более отрицательный настрой ей отвечает (отметим, что определение направления "возрастания" шкальных значений наших объектов весьма условно: увеличение их может происходить как справа налево, так и наоборот, надо только четко оговорить, какой вариант мы выбираем).