ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 26.10.2023
Просмотров: 346
Скачиваний: 5
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Таким образом, наше предположение об однородности состоит в интерпретации совокупности оценок, отвечающих одному суждению, не как совокупности оценок, данных разными экспертами, не как совокупности шкальных значений респондентов, с этим суждением согласных (а выше мы делали оба эти
Ясно, что в таком случае интервалы между суждениями не будут равны: s2 — > s3 — s2.Но чем мельче отвечающие разным
предположения), а как совокупности оценок, данных этому суждению одним респондентом при разных условиях опроса. Ясно, что каждая такая совокупность отвечает порядковой шкале.
Теперь рассмотрим, что происходит в сознании одного эксперта при размещении им суждений по ячейкам.
Рассмотрение ячеек как интервалов числовой оси
Известный, использованный Терстоуном способ расчета медиан (с помощью кумуляты) предполагает, что каждый эксперт, относя суждение к той или иной категории, указывает не отдельную точку оси, а некоторый ее интервал. Медиана какого-либо суждения вполне может оказаться равной, скажем, не 5 или 6, а 5, 8. А то, что эксперт не указывает точное местонахождение суждения в том или ином интервале, означает, что он по каким-то причинам не может этого сделать. Сказанное станет более ясным позже, когда мы приведем пример расчета медианы.
Гипотеза о равенстве расстояний между суждениями, отнесенными к соседним ячейкам
Применим к рассматриваемому случаю соображения, высказанные в п. 1.2.
Эксперты, раскладывая суждения по ячейкам (категориям), фактически не приписывают им никаких чисел. Они говорят только об относительном порядке этих суждений и совсем не утверждают того, что, например, первой ячейке отвечает число 1, второй — число 2 и т.д. Если мы хотим строить шкалу, адекватно отражающую реальность, не надо додумывать за респондента, не надо навязывать реальности числа там, где они не возникают естественным образом. Точнее, не надо навязывать респонденту число, когда явно мы не требуем от него никакой числовой оценки (рекомендуем читателю сравнить сказанное также и с приведенными далее, в гл. 9, рассуждениями по поводу метода одномерного развертывания).
Тем не менее обходиться совсем без модельных представлений вряд ли возможно. Особенно если мы хотим достичь интервального уровня измерения. Опишем, какие элементы моделирования представляются нам более разумными, чем рассмотрение номеров ячеек как чисел.
Обеспечение интервальное™ строящейся шкалы, как следует из соответствующего определения (п. 1.1), сопряжено с умением выявлять, равны ли те или иные отрезки используемого нами континуума (точнее, стоит ли что-нибудь реальное за очевидными арифметическими равенствами).
В литературе при описании метода построения шкалы Терстоуна часто говорится о том, что при размещении суждений по ячейкам эксперт должен стремиться к тому, чтобы расстояния между суждениями, отнесенными к соседним ячейкам, были одинаковыми. Нам это требование представляется помехой построению такой шкалы, которая адекватно отражала бы истинные настроения респондентов.
Во-первых, эксперт далеко не всегда может определить, одинаковы расстояния между какими-либо суждениями или нет. Во-вторых, даже если предположить, что проблема определения расстояний между суждениями экспертом решена, у нас нет никакой гарантии, что среди рассматриваемых суждений найдутся хотя бы какие-то, равноотстоящие друг от друга.
Т
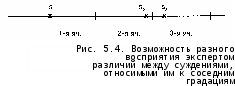
ем не менее все же нередко мы можем допустить, что суждения, отнесенные к соседним ячейкам, равноотстоят друг от друга. Правомерность такого допущения связана с определением количества используемых ячеек: если мы хотим, чтобы получаемую шкалу можно было считать интервальной, требуется, чтобы это количество было относительно большим. Вполне может быть, что некий эксперт, поставив на первое место суждение srна второе — s2, на третье — s3, руководствовался (может быть, даже не давая себе в этом отчета), скажем, следующим расположением этих суждений на нашей латентной оси (рис. 5.4).
интервала равной единице, а можем длину отрезка считать равной 5500, начинать откладывать интервалы от 1000 и длину каждого полагать равной 500 (см. рис. 5.5).

градациям интервалы, тем более незначительным будет указанное неравенство. И им в конце концов можно будет пренебречь.
Кроме того, человеку трудно дифференцировать свои представления о большом количестве качественно различных состояний какой-либо переменной. Это тоже дает основания считать расстояния между суждениями, отнесенными к соседним градациям, одинаковыми.
Именно поэтому стремление получить интервальный уровень измерения за счет обеспечения хотя бы приблизительного равенства расстояний между соседними градациями шкалы заставляет исследователя использовать как можно большее число градаций.
Отметим, однако, что количество градаций не должно быть слишком большим. Эксперты должны быть способны держать в голове всю ранжировку сразу на каждом этапе ее формирования.
Вероятно, именно количество ячеек, равное 11, может удовлетворить обоим нашим требованиям.
Неоднозначность совокупности рангов, приписанных суждениям одним экспертом
Выше мы фактически показали, что ранги, приписанные рассматриваемым суждениям одним экспертом, можно считать полученными по шкале более высокого типа, чем порядковая по интервальной шкале (поскольку для этих рангов осмыслены равенства разностей). Покажем, что эти ранги не являются числами в общепринятом смысле этого слова, что они определены не однозначно, а лишь с точностью до таких преобразований, которые равные интервалы переводят в равные (другими словами, покажем, что полученная шкала не может расцениваться как шкала более высокого типа, чем интервальная; о таких шкалах пойдет речь в главе 14).
Сделанные выше предположения означают, в частности, что при определении номера ячейки, подходящей для того или иного суждения, эксперт мысленно видит фрагмент числовой оси, разделенный на 11 равных интервалов, и должен выявить, к какому из этих интервалов суждение относится. При этом не фиксируются ни место отрезка на прямой, ни его длина. Респондент об этом не думает! И поэтому наша модель не должна включать в себя соответствующих уточнений.
Для анализа результатов работы экспертов мы можем использовать, например, отрезок от 0 до 11, считая длину каждого
Поскольку мы предполагали, что, ранжируя суждения, все респонденты "работают" в одной и той же шкале (точнее, что совокупность оценок одного суждения разными экспертами можно считать исходящими от одного человека), то естественно предположить, что, на каком бы наборе интервалов типа тех, что представлены на рис. 5.4, мы ни остановились, он будет единым для всех экспертов.
Интервальность шкалы, построенной для оценки суждений
Конечно, говоря о расчете медиан, мы не можем не приписывать суждениям какие-то числа. Но в соответствии со сказанным выше сделать это можно по-разному в зависимости от того, какой длины интервалы будем использовать и какова наша точка отсчета.
Нетрудно показать, что при переходе от одной возможной шкалы к другой (имеются в виду шкалы типа тех, что изображены на рис. 5.5) совокупность медиан, рассчитанных для всех рассматриваемых суждений тоже претерпит изменение, отвечающее интервальной шкале: хотя все значения медиан изменятся, но структура интервалов между ними сохранится. Если бы неоднозначность совокупности медиан объяснялась только указанной неоднозначностью исходных данных, то можно было бы считать доказанной интервальность той шкалы, по которой получены наши медианы. Но совокупность значений медиан может измениться еще по одной причине.
Дополнительную неоднозначность искомым медианам придает то, что кумулятивный процент можно откладывать от раз-
ных мест соответствующего интервала, на' практике чаще всего его откладывают либо от середины, либо от какого-нибудь из его концов. Приведем пример того, как итоговая медиана изменяется в зависимости именно от последнего обстоятельства. Пусть имеются данные, представленные в табл. 5.2.
Таблица 5.2. Результатыгипотетического
экспертногоопроса
| № ячейки | 1 2 3 4 5 |
| % экспертов, поместивших суждение в ячейку | 20 10 25 30 15 |
Следуя технике, предлагаемой в [Паниотто, Максименко, 1982], где первой ячейке отвечает интервал (0, 1), а величина процента суждений, попавших в эту ячейку, откладывается от середины интервала, мы получим медиану, которая будет равна 2, 2 (рис. 5.6). Если же следовать технике, предложенной в [Рабочая книга..., 1982], отличающейся от предыдущей тем, что величина упомянутого процента откладывается не от середины, а от правого конца интервала, то получим картину, изображенную на рис. 5.7. Медиана в этом случае окажется равной 2,7. И так для любой медианы. Все медианы при соответствующем пересчете сдвинутся на 0,5 вправо.
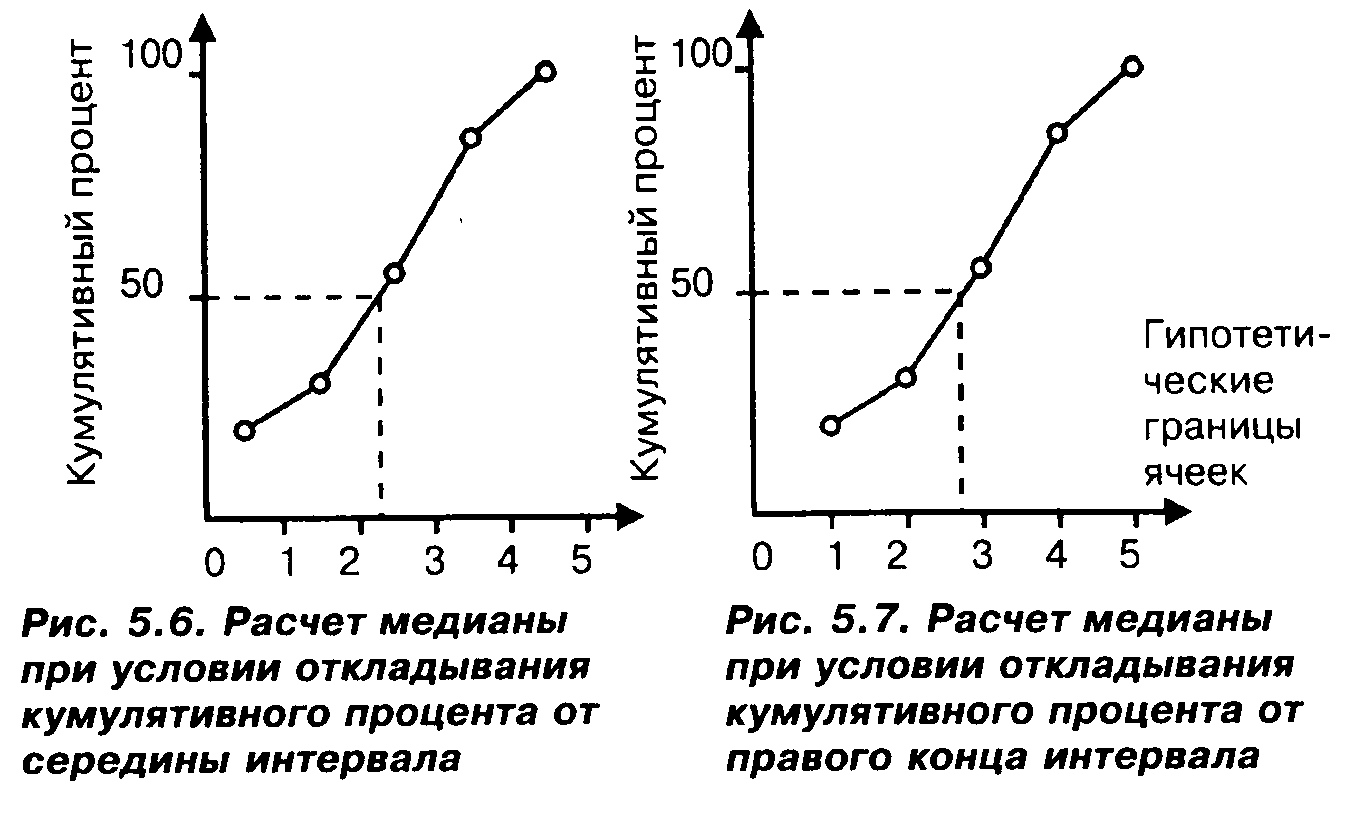
Ясно, что если, скажем, мы будем откладывать единичные интервалы не от 0, а от 1, то получим для тех же данных значения медиан, равные 3,2 и 3,7, и т.д. И все медианы сдвинутся по сравнению с ситуацией, изображенной на рис. 5.6, на 1 в первом случае и на 1,5 — во втором. Естественно, структура интервалов между медианами, как и выше, не изменится.
Если наши интервалы изменятся по длине (вспомним рис. 5.5), то все медианы уменьшатся (увеличатся) в соответствующее число раз, но структура интервалов между медианами останется той же. Таким образом, если исходные ранги получены по интервальной шкале, то и совокупность медиан (значений наших суждений) можно будет считать полученной по интервальной шкале.
Иншервальность установочной шкалы Терстоуна
Теперь попытаемся обосновать тот факт, что при использовании предложенной Терстоуном техники мы действительно получаем интервальную шкалу. Подведем итог сказанному выше.
Напомним, что мы сочли возможным считать все оценки-ранги, отвечающие одному суждению, полученными как бы от одного человека. При этом было показано, что соответствующую шкалу можно считать интервальной (за счет осмысленности равенства разностей между рангами). Истинное мнение такого обобщенного человека об указанном суждении отвечает медиане этих суждений, разброс имеет место за счет каких-то случайных флуктуации.
Далее мы показали, что медианы разных суждений можно считать полученными по интервальной шкале (поскольку совокупность таких медиан была определена так же, как и совокупность тех рангов, из которых медианы получались, — с точностью до структуры интервалов между ними). При этом фактически было доказано более общее положение ("теорема"): если у нас имеется ряд распределений случайных величин, все значения которых можно считать полученными по одной и той же интервальной шкале, то совокупность медиан этих распределений тоже можно считать полученной по интервальной шкале.
Совокупность медиан суждений, отмеченных каким-либо одним респондентом, при его опросе на третьем этапе построения шкалы, мы также считаем случайным образом разбросанными оценками того, что мы ищем, — значения изучаемой установки этого респондента. Медиана этих оценок — шкальное значение респондента. Каждому респонденту отвечает свой "разброс". Таким образом, совокупность итоговых шкальных значений наших респондентов — это совокупность медиан распределений случайных величин, значения которых в свою очередь являются полученными по интервальной шкале медианами. Интервальность этой шкалы вытекает из сформулированной выше "теоремы".
Резюмируя все сказанное выше, можно заметить, что в качестве дополнительных предположений об изучаемой ЭС (тех, которые служат заменой непосредственного измерения сложных отношений, отображение которых в числа требуется для получения интервальной шкалы, см. п. 3.1) в данном случае фигурируют все сделанные выше предположения о свойствах ответов наших респондентов: об однородности совокупности экспертов; о равенстве расстояний между суждениями, отнесенными к соседним ячейкам; о неоднозначности совокупности рангов, приписанных разным суждениям одним респондентом, и т.д.
Перейдем к рассмотрению метода построения оценочной шкалы, основанного на схожих предположениях. Идея метода также принадлежит Терстоуну.
1 2 3 4 5 6 7 8 9 ... 14
Глава 6. МЕТОД ПАРНЫХ СРАВНЕНИЙ (ПС)
Итак, метод парных сравнений — это метод построения оценочной шкалы. Вариант, предложенный Терстоуном, представлял собой довольно узкий подход к шкалированию. Но в настоящее время соответствующие идеи, будучи расширенными, привели к созданию довольно мощной ветви прикладной статистики [Адлер, Шмерлинг, 1978; Дэвид, 1978]. Здесь мы имеем иллюстрацию к упомянутому в п. 3.3 положению: содержательные (здесь — социально-психологические) идеи, будучи четко сформулированными (с использованием математического языка), дали толчок развитию соответствующей математической теории, которая затем начала возвращаться в содержательную область, породившую исходные идеи.
Прежде чем описывать метод, необходимо сказать несколько слов о термине "метод ПС". Дело в том, что в литературе он используется в двух смыслах: в узком и широком. Коротко рассмотрим, в чем здесь дело.
Строго говоря, метод ПС — это метод получения исходных данных, метод своеобразного опроса респондентов. Этот метод будет описан нами в п. 6.1. Соответствующее использование ин-тересущего нас термина отвечает его узкому смыслу. На базе полученных данных можно решать разные задачи, совсем необязательно включающие в себя построение оценочной шкалы. Построение такой шкалы — это лишь одна из возможных задач.
В литературе то же самое название (метод ПС) употребляется также для обозначения широкого круга методов, включающих в себя не только упомянутый выше метод сбора данных, но и способы построения на его основе оценочной шкалы. Такое использование термина отвечает определенному нами широкому смыслу, который отражен в основном в п. 6.2.
6.1. ПС как метод сбора данных
6.1.1. Содержаниеметода.
Свойстваполучаемыхматриц
Выше мы говорили о недостатках, с которыми сопряжено получение оценочной шкалы на базе либо прямых числовых оценок респондентами шкалируемых объектов, либо ранжировок. В психологии показано, что большего доверия заслуживает несколько иной метод сбора данных — так называемый метод парных (попарных) сравнений шкалируемых объектов. Суть его состоит в следующем.
Предположим, что нас интересует, как респонденты изучаемой совокупности оценивают какие-либо объекты — профессии, политических лидеров, радиопередачи, какие-то виды товаров и т.д. Обозначим эти объекты через а/; a2, ...,αη(η— количество оцениваемых объектов). Рассматриваемый метод позволяет получить ответ на этот вопрос в довольно своеобразном виде. Каждому респонденту предлагаются всевозможные пары, составленные из рассматриваемых объектов. Он должен относительно каждой пары сказать, какой объект из этой пары ему нравится больше. Скажем, в случае рассмотрения в качестве наших объектов некоторых профессий — к примеру, токаря, пекаря, лекаря и т.д. — мы спрашиваем у каждого респондента, какая профессия ему больше нравится: токарь или пекарь (фиксируем ответ), токарь или лекарь (фиксируем ответ), пекарь или лекарь (фиксируем ответ) и т.д. для всех возможных пар рассматриваемых объектов.
Полученные таким образом данные обычно сводятся в квадратную матрицу из 0 и 1, число строк и столбцов которой равно числу рассматриваемых объектов и элементы которой получаются следующим образом: на пересечении г'-й строки иу'-го столбца такой матрицы стоит 1, если i-Piобъект нравится рассматриваемому респонденту больше, чем у'-й, и стоит 0, если, напротив, у'-й объект респонденту более симпатичен, чем /-й (вместо выражения "больше нравится" здесь, в зависимости от задачи, могут фигурировать словосочетания "больше", "красивее", "более престижен", "больше подходит" и т.д.). Будем называть такую матрицу матрицей парных сравнений.
Ниже вместо выражений типа "объект а. лучше объекта а" будем использовать выражение "а > а". В общем виде матрицу для респондента г, (I = 1, ..., N,где N—количество респонден
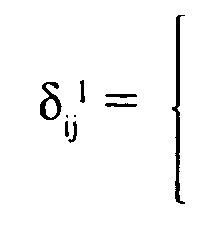
тов) обозначим через ||δ '||, где
1, если респондент η сказал, что а; > я ,
О, если респондент η сказал, что а. < а .
В качестве примера такой матрицы см. табл. 6.1.
Таблица 6.1. Примерматрицыпарныхсравнений, полученнойотодногореспондента
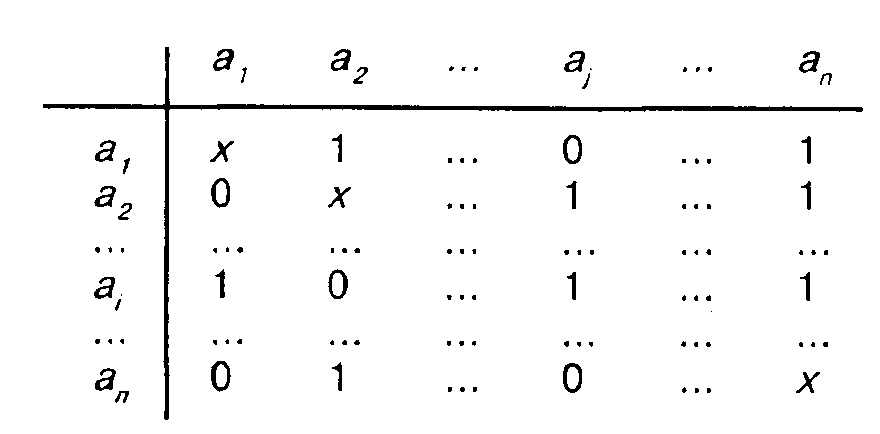
По главной диагонали матрицы нами проставлены крестики, поскольку мы считаем, что сам с собой объект не сравнивается. Нетрудно проверить, что суть отраженной с помощью этой матрицы информации обусловливает некоторые формальные свойства матрицы.
Во-первых, она должна быть асимметричной: если на пересечении /'-й строки и у'-го столбца стоит 1 (0), то на пересечении у'-й строки и /-го столбца должен стоять 0(1). Мы видим, что это свойство выполняется для матрицы, изображенной на рис. 6.1. Так, на пересечении первой строки и последнего столбца у нас стоит 1. Это означает, что первый объект нравится нашему респонденту больше, чем последний. В таком случае естественно ожидать, что последний объект будет ему нравиться меньше, чем первый, и, следовательно, на пересечении последней строки и первого столбца матрицы должен стоять 0, что и имеет место.
Во-вторых, матрица должна удовлетворять условию транзитивности: если некий объект ajнравится респонденту больше, чем а;, а а. больше, чем ак, то естественно ожидать, что объект а будет ему нравиться больше, чем ак. Так, на нашем рисунке можно видеть, что первый объект нравится рассматриваемому респонденту больше второго (на пересечении первой строки и второго столбца стоит 1), а второй — больше последнего (на пересечении второй строки с последним столбцом* стоит 1). Естественно ожидать, что первый объект будет нравиться респонденту больше, чем последний, что и отражает матрица, поскольку в ней на пересечении первой строки и последнего столбца стоит 1.
В то, что результаты парных сравнений заслуживают большего доверия, чем, скажем, ранжировка, можно поверить: встав на точку зрения респондента, нетрудно понять, что проранжи-ровать все объекты иногда бывает весьма трудно, в то время как попарно их сравнить гораздо легче.
Метод ПС дает результаты, иногда весьма отличные от метода ранжирования. Мы неоднократно проводили эксперименты со студентами-социологами: с некоторым разрывом во времени просили их сначала попарно сравнить некие объекты, а потом про-ранжировать их же. Результаты весьма отличались друг от друга (и это — для будущих профессионалов, рефлексирующих по поводу того, что они делают, что же ожидать от "простых" респондентов, далеких от науки?). Более того, много раз оказывалось невозможным на базе парных сравнений построить ранжировку. Ниже, в п. 6.1.3, мы рассмотрим возможные причины возникновения такой ситуации.
6.1.2. Ограниченияметода
Следует отметить, что описанный выше подход к получению данных методом ПС не учитывает многих особенностей восприятия респондентом предлагаемых ему объектов. Так, мы полагали, что респондент всегда может однозначно оценить, какой из любых двух рассматриваемых объектов ему более симпатичен. А ведь на практике это далеко не всегда соблюдается. Так, оценивая, к примеру, какая профессия — токарь или пекарь — ему больше нравится, респондент может оказаться в затруднительном положении: с одной стороны, вроде бы любит он токарными работами заниматься, а с другой — пекарю больше платят, и т.д.
В ситуации, подобной описанной, нюансы могут быть разными: респондент может считать рассматриваемые объекты несравнимыми, а может полагать, что они равны. Но в любом случае нам оказывается недостаточно двух чисел (меток) — 0 и I — для описания всех таких нюансов. Так, уже для описанного случая подобных меток должно быть по крайней мере четыре: "больше", "меньше", "равны", "не сравнимы". Возможны и другие ситуации. Так, зачастую бывает целесообразно учесть возможность различной степени уверенности респондента в том, что один объект лучше другого. В таком случае становится естественным введение совокупности меток, например множества действительных чисел от 0 до I, когда каждое число отвечает соответствующей степени уверенности. Заметим, что подобные обобщения — одна из причин того, что сравнительно простой подход, предложенный Терстоуном, к настоящему времени разросся в огромное направление прикладной статистики.
Еще одно ограничение рассматриваемого подхода к сбору данных связано с тем, что мы часто бываем вынуждены мириться с наличием логических противоречий в описанных выше матрицах из 0 и I — нарушением условий асимметричности и транзитивности. Но об этом — в следующем пункте.
6.1.3. ПСкакшкальныйкритерий
Будем говорить, что метод построения одномерной шкалы может служить шкальным критерием, если с его помощью можно достичь одной из двух целей: либо построить требующуюся шкалу, либо показать, что одномерная шкала в рассматриваемой ситуации в принципе не может быть построена.
Отметим, что далеко не каждый метод шкалирования может служить в качестве шкального критерия. Многие методы формально приведут нас к некоторой "шкале" даже в тех случаях, когда это совершенно бессмысленно. Конечно, такой шкалой пользоваться нельзя. Но мы можем даже не узнать об этом. Поэтому методы шкалирования, могущие служить в качестве шкального критерия, представляются весьма важными для социолога. Покажем, каким образом и в каких ситуациях метод ПС (пока мы понимаем его в узком смысле) поможет нам выяснить, что построение искомой шкалы бессмысленно.
Речь пойдет об упомянутых выше логических противоречиях. При этом мы для простоты не будем учитывать то, что респондентов у нас много и каждому из них, вообще говоря, отвечает своя матрица парных сравнений. Будем пока считать, что респондент у нас один (о проблеме соотнесения друг с другом матриц, отвечающих разным респондентам, см. п. 6.2.1).
Рассмотрим, как логические противоречия могут быть связаны с существованием интересующей нас шкалы. Проанализируем два аспекта такой связи.
Во-первых, покажем, что при нарушении свойств асимметричности и транзитивности построение искомой оценочной шкалы оказывается логически невозможным. Действительно, такое построение означает размещение рассматриваемых объектов на числовой оси (напомним, что числовая ось отвечает искомой латентной переменной, которую можно назвать, к примеру, "престижность профессии", "привлекательность политического лидера" и т.д.) таким образом, чтобы при этом удовлетворялись те соотношения между объектами, которые отражены в исходной матрице ПС. И если в этой матрице на пересечении /-й строки иу-го столбца стоит 1, т.е. aj> α, то первый объект на оси должен быть расположен правее второго. И совершенно ясно, что это никак не может сочетаться с тем, что а > д., что должно было быть выполненным, если бы в той же матрице ПС единица стояла на пересечении у'-й строки и г'-го столбца (т.е. если бы матрица была симметричной).
То же можно сказать и о свойстве транзитивности матрицы. При его нарушении оказывается невозможным нахождение шкальных значений рассматриваемых объектов: как ни располагай их на числовой оси, никак нельзя сделать так, чтобы одновременно выполнялись соотношения, отвечающие неравенствам а. > а., я > оки α < ак.
Итак, нарушение свойств асимметричности и транзитивности для исходной матрицы ПС влечет невозможность построения адекватной этой матрице одномерной шкалы для рассматриваемых объектов. Но в действительности рассматриваемая ситуация не всегда приводит социолога к отказу от построения шкалы. Здесь вступает в силу некоторое эвристическое правило, к сожалению, очень часто требующееся на практике. Оно состоит в том, что если некоторый метод становится некорректным при несоблюдении определенных условий, то мы все же его используем, когда эти условия нарушены в небольшой мере. Если же нарушения велики, то мы отказываемся от использования метода. При этом смысл слов "большой" или "небольшой" применительно к количеству нарушений — субъективен. Исследователь может определить границу между ними, только опираясь на практический опыт реализации рассматриваемого метода и осуществления на базе полученных результатов тех или иных прогнозов с последующей их проверкой.
Социолог вынужден следовать только что сформулированному правилу. Отказ от него привел бы к невозможности использовать практически любые методы измерения и анализа данных почти в каждом социологическом исследовании, поскольку условия применимости любого метода в социологии практически всегда бывают нарушены.
В нашем случае обсуждаемое правило означает, что если в исходной матрице ПС мало нарушений асимметричности и транзитивности, то, несмотря на их наличие (а какое-то количество нарушений бывает практически всегда), мы все же будем строить искомую одномерную шкалу. Если же подобных нарушений много, то мы вынуждены прийти к выводу о невозможности построения для наших объектов требующейся одномерной шкалы. Встает вопрос о том, какие содержательные причины (очевидно, обусловленные спецификой восприятия респондентом предлагаемых ему для сравнения объектов) стоят за такой невозможностью. Чтобы ответить на него, рассмотрим второй аспект связи противоречий в матрице ПС с существованием обсуждаемой шкалы.
Итак, во-вторых, покажем, какие особенности восприятия респондентом наших объектов стоят за нарушением асимметричности и транзитивности матрицы ПС.
Приведем пример одной из возможных причин возникновения нетранзитивности. Представим, что респондент, сравнивая профессии токаря и пекаря, пришел к выводу, что быть пекарем лучше, чем токарем, поскольку пекарь — при продуктах питания, что в наше время немаловажно. Пусть также, сравнивая профессии пекаря и лекаря, он пришел к выводу, что лекарь лучше, поскольку работа по этой профессии дает доступ к более дефицитным товарам. А в ситуации сравнения профессий токаря и лекаря наш респондент вдруг задумался о тех заработках, которые он будет иметь, и понял, что токарь-то получает больше и, стало быть, профессия токаря лучше. Вот и нетранзитивность!
В чем же причины нарушения транзитивности? Вряд ли стоит обвинять респондента в нелогичности мышления или глупости. Дело в другом — в том, что, сравнивая объекты, он учитывал несколько оснований, используя то одно, то другое. Другими словами, "корень зла" в том, что мышление респондента, его восприятие интересующих нас профессий — многомерно! Человек не столь примитивен, как этого требует одномерная шкала.
К такому же выводу можно прийти и при анализе возмржных причин нарушения асимметричности матрицы ПС.
Таким образом, наличие в исходной матрице ПС рассматриваемых нарушений логики может говорить о необходимости пе^ рехода к многомерному шкалированию (о том, что это такое, было сказано в п. 1.3).
6.2. ПС как метод построения оценочной шкалы
Перейдем к рассмотрению метода парных сравнений, понимая его в широком смысле. Итак, нашей "сверхзадачей" является приписывание рассматриваемым объектам таких чисел Vп У2, Vn, которые можно было бы рассматривать как выражение усредненного (суммарного) мнения наших респондентов об этих объектах. Исходные данные — совокупность матриц ПС, полученных от респондентов. Количество таких матриц, естественно, равно количеству респондентов.
Метод ПС принадлежит к числу таких методов, относительно которых трудно решить, к какой области их отнести: к теории измерений или к анализу данных. С одной стороны, конечно, речь идет об измерении — о приписывании чисел рассматриваемым объектам, но, с другой — о способе анализа первичных данных совокупности матриц из 0 и 1 — с целью получения новой информации, новых сведений о рассматриваемых объектах.
Будем говорить о методе ПС как о методе анализа данных и в соответствии с этим используем ту (кибернетическую) терминологию, которая, как нам кажется, полезна для формирования у читателя четкого представления о сути метода.
Входом метода служит совокупность полученных от респондентов матриц ПС, выходом — совокупность чисел, приписанных шкалируемым объектам. Естественно, вход и выход должны быть опосредованы некоторой идеей, отражающей наше видение того, что, собственно, такое искомые числа и как они связаны с исходными парными сравнениями. И эта идея, вероятно, должна опираться на некоторые модельные концепции, в основе которых должны лежать наши априорные представления о восприятии отдельным респондентом изучаемых объектов и о том, что такое агрегированное мнение об этих объектах всех респондентов сразу.
Схематически суть метода можно выразить следующим образом:
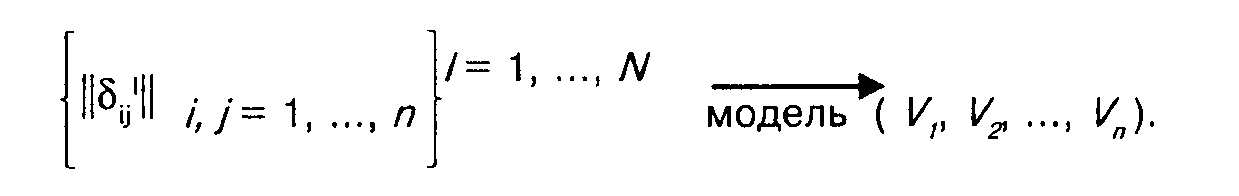
В литературе предложены разные модели интересующего нас плана. Это лишний раз доказывает высказанное нами в п. 3.3 положение о том, что любые явления, интересующие социолога, при тщательном их рассмотрении, при попытке уточнить их сущность возможно описать с помощью разных формальных схем.
В нашем случае мы прежде всего рассмотрим серию моделей, предложенных основоположником метода ПС — Терстоуном. Опишем эти модели довольно подробно. Представляется, что это даст возможность читателю не только познакомиться с теми результатами, которые стали уже классическими, но и получить более полное представление о том, каковы здесь модели восприятия. Эти модели (в отличие от моделей, заложенных в методе построения установочной шкалы, описанных нами в п. 5.2) достаточно ярко описаны самим автором.
Последнее замечание, которое нам хотелось бы высказать, прежде чем перейти к описанию конкретных моделей, касается роли математики в развитии арсенала методов социологического исследования. Дело в том, что метод ПС являет собой яркий пример того, как достаточно четкая формулировка автором метода исходных содержательных позиций (с использованием языка математики) привела сначала к активному углублению и развитию соответствующих положений средствами математики, а затем к обогащению теории социологического измерения. Следуя Терстоуну, мы попытаемся довольно активно (хотя и с учетом того, что наша работа адресована в первую очередь гуманитариям) использовать для описания интересующих нас моделей математический язык.
6.2.1. МоделиТерстоуна
Итак, нам надо понять, какова суть тех шкальных значений, которые мы хотим найти. Что мы, собственно, ищем?
Представление о мнении одного респондента об одном объекте
Начнем издалека. Зададимся вопросом о том, что из себя представляет мнение одного респондента об одном объекте.
Выше (в п. 5.2) мы говорили о том, что такое плюрализм мнения человека о каком-либо объекте. Вспомним соответствующее определение и будем считать, что мнение каждого респондента о любом из шкалируемых нами объектов является плюралистичным. Ссылаясь на практику, мы отмечали, что конструктивно такое предположение может использоваться только в том случае, если оно формулируется строго, с использованием математического языка, и упоминали примеры такого рода формулировок. Еще одним примером конструктивного подхода к определению интересующей нас плюралистичности и формированию на его основе практических рекомендаций является модель Терстоуна парных сравнений. Опишем ее.
Предположим, что у нас имеются объекты αμа2, апи респонденты грг2,rN.Предположим, что мнение одного респондента г, об одном объекте а.(1 — любое число из множества 1, 2,
N;i—любое число из множества 1, 2, п)представляет собой нормальное распределение (см. рис. 6.1).
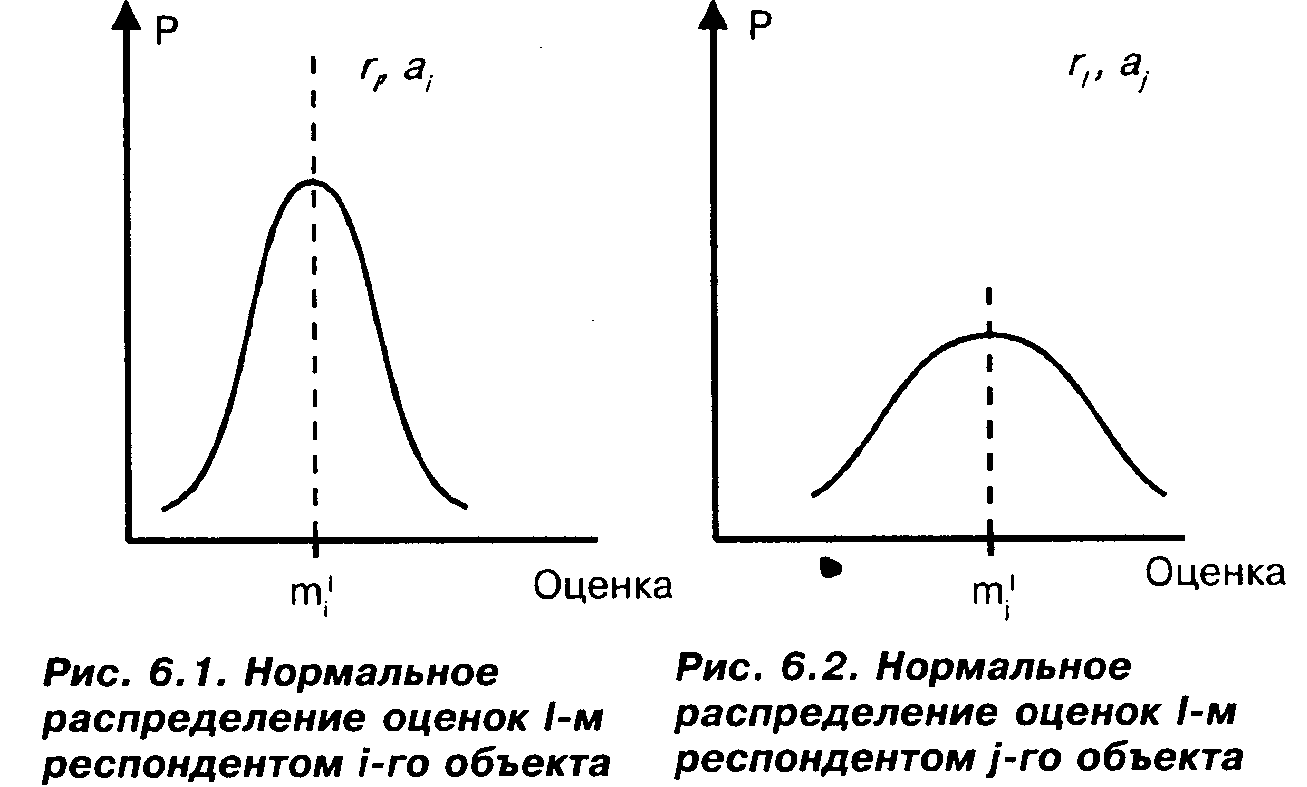
Проще говоря, это означает, что- при опросах, производящихся в разных условиях, наш "градусник" чаще всего будет показывать некоторую оценку т!(математическое ожидание, т.е. среднее значение нашего нормального распределения), реже — другие оценки. И чем дальше какое-либо число отстоит от т], тем реже оно будет встречаться в качестве такой оценки.
На рис. 6.2 изображено аналогичное распределение для того же респондента и другого объекта. Естественно, величины т!и т!, вообще говоря, будут различными, поскольку разные объекты респондент, вероятно, "в среднем" оценивает по-разному.
Вероятно, естественным выглядит предложение считать "истинной" оценкой мнения нашего респондента о рассматриваемом объекте соответствующее математическое ожидание. Оказывается, что и дисперсию рассматриваемых распределений можно проинтерпретировать естественным образом (напомним, что нормальное распределение однозначно задается значениями математического ожидания и дисперсии либо среднего квадрати-ческого отклонения). Покажем это.
Рассмотрим рис. 6.3, на котором изображены интересующие нас распределения, отвечающие разным дисперсиям.
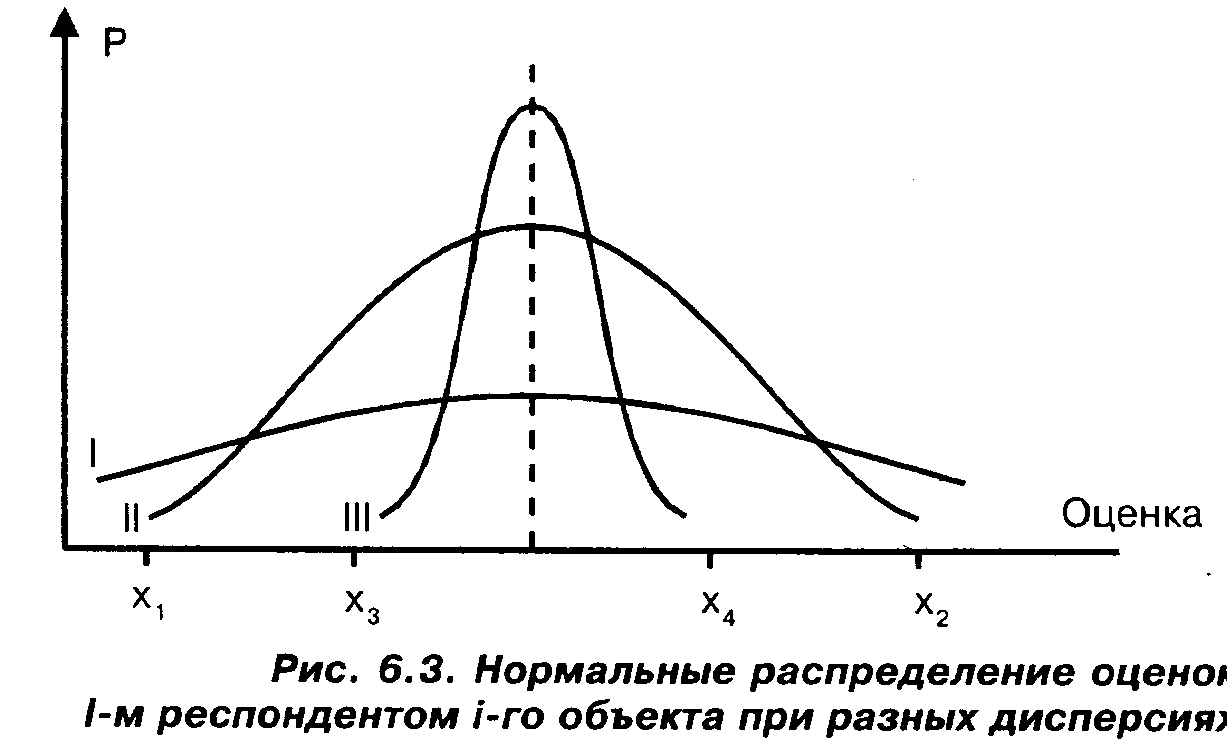
Нетрудно понять, что дисперсия говорит о степени уверенности (убежденности) респондента в своем мнении о рассматриваемом объекте. Если это мнение определяется распределением I, то респондент, будучи опрошенным в разное время, примерно с одинаковой вероятностью будет давать совершенно различные ответы, в том числе и весьма отличающиеся от среднего. Так, значения xiи хгв его ответах могут встретиться почти с той же вероятностью, что и среднее значение.
Если мнение респондента определяется распределением III, то, напротив, значения, даже незначительно отличающиеся от среднего, такие, как х, и х4, будут встречаться с гораздо меньшей вероятностью, чем само среднее. А вероятность получить от респондента ответы χίи х2будет практически равна 0.
При использовании распределения II ситуация будет занимать промежуточное положение между двумя описанными выше.
Ясно, что упомянутая степень уверенности может быть объяснена разными факторами: характером (принципиальностью)
респондента, его знанием оцениваемых объектов, важностью этих объектов для респондента и т.д.
Пока будем считать, что дисперсии тех распределений, которые отвечают мнениям одного респондента о разных объектах, вообще говоря, различны. Так, различны дисперсии распределений, приведенных на рис. 6.1 и 6.2. Теперь перейдем к обсуждению вопроса: должны ли быть схожими, и, если должны, то в какой степени, распределения, отвечающие разным респондентам? Чтобы наша задача была осмысленна, и здесь (так же, как и в случае установочной шкалы Терстоуна) требуется определенная однородность изучаемой совокупности респондентов.
Однородность совокупности респондентов
Рассмотрим, как соотносятся распределения, отвечающие мнениям разных респондентов об одном и том же объекте. Покажем, что смысл задачи заставляет нас считать равными средние значения соответствующих распределений.
Другими словами, предположим, что, будучи опрошенными много раз, наши два респондента в среднем будут давать разные
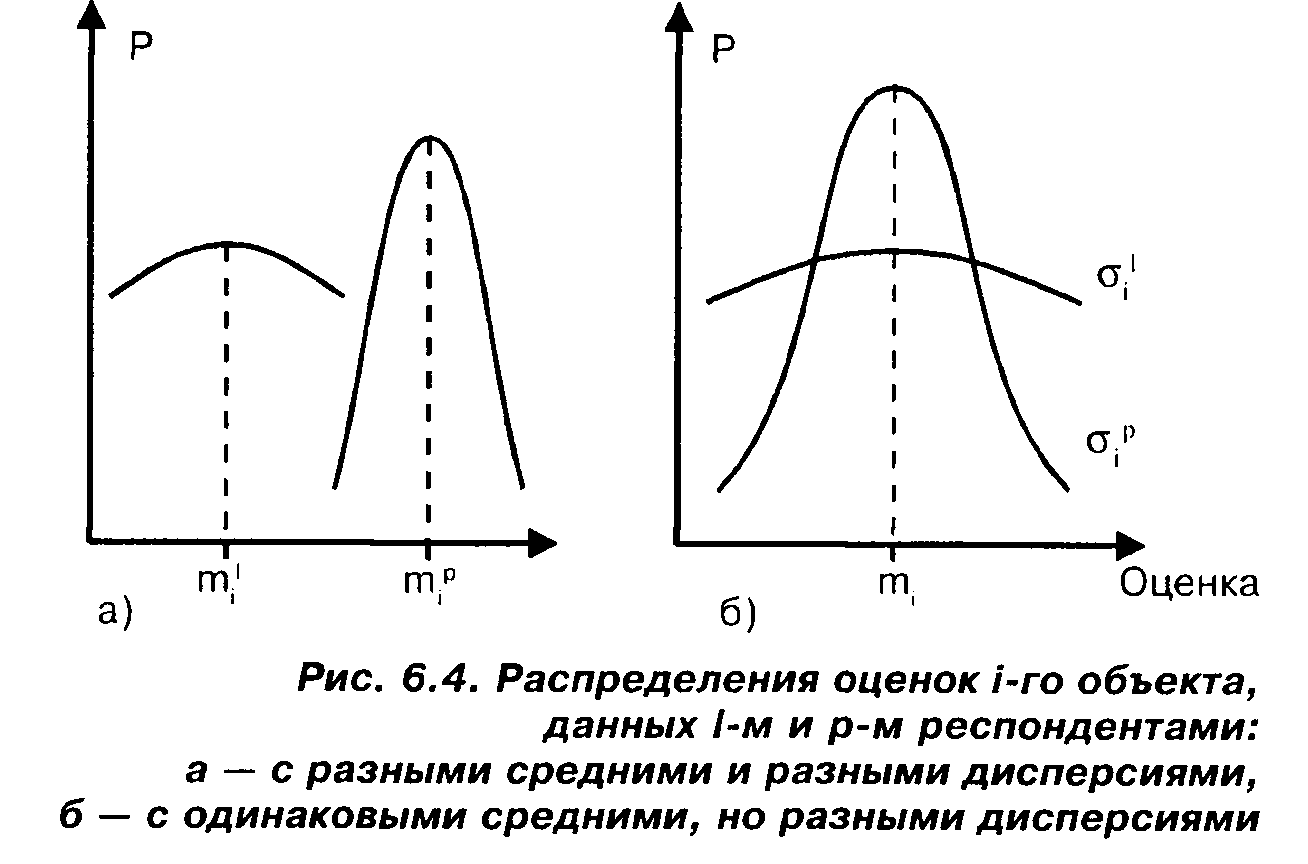
Предположим, что упомянутого равенства нет, будем считать, что мы имеем дело с ситуацией, отраженной на рис. 6.4 а.
оценки. Скажем, если речь идет об оценке политического лидера — то оценки /-го респондента в среднем низки, а р-το—в среднем высоки. Будет ли в таком случае осмысленной наша главная задача — приписывание лидеру такого числа, которое отразило бы суммарное, усредненное мнение наших респондентов? Наверное, нет. Соответствующее среднее мнение так же будет лишено смысла, как пресловутая "средняя температура по больнице".
Наверное, любой добросовестный социолог при наличии в изучаемой совокупности таких респондентов, мнение которых отвечает распределениям, изображенным на рис. 6.4 а, придет к выводу, что среди интересующих его людей мнения относительно рассматриваемого лидера разделились: одним респондентам этот лидер нравится, другим — нет. И прежде чем осуществлять шкалирование, вероятно, такой социолог сочтет разумным разделить всю совокупность на две и для каждой из полученных подсовокупностей искать среднюю оценку отдельно. В итоге мы получим две оценки: среди интересующего нас множества людей имеются такие, которые одобряют рассматриваемого лидера и их средняя оценка — такая-то, но имеются и те, кто не одобряет его, и их средняя оценка — другая.
Ставя вопрос в более общем виде, можно сказать, что в описанной ситуации исходная совокупность респондентов недостаточно однородна для того, чтобы к ней мог быть применен метод парных сравнений, и для того, чтобы такое применение было осмысленным, необходимо в исходной совокупности выделить однородные подсовокупности.
Вероятно, разумно предположить, что в нашем случае однородность совокупности респондентов определяется равенством не только средних соответствующих распределений, но и соответствующих дисперсий. Действительно, представим себе, что каким-то двум респондентам отвечают распределения, изображенные на рис. 6.4 б, где σ," и σ' — средние квадратические отклонения (напомним: для получения дисперсий надо их возвести в квадрат), отвечающие р-му и 1-му респондентам соответственно. Один из них (р-й) хорошо знает рассматриваемого политического лидера и поэтому уверен в своих оценках. Его дисперсия мала, кривая "узка", вероятность дать ответ, сильно отличающийся от среднего, практически равна нулю. Напротив, другой респондент (1-й)имеет об упомянутом политике весьма смутное представление. Ему более или менее все равно, какие оценки давать. Весьма сильно разнящиеся ответы могут встретиться примерно с одинаковой вероятностью. Наверное, построение оценки, средней для таких двух респондентов, тоже будет сомнительным.
Итак, будем считать, что наша совокупность однородна, т.е. что распределения, отвечающие одному объекту, но разным респондентам, одинаковы (т.е. имеют одинаковые средние и дисперсии). Значит, в обозначениях математических ожиданий (средних) и средних квадратических отклонений этих распределений можно убрать индексы, отвечающие номеру респондента: т! = =mf = т(; σ' = ογ = σ .
Следует отметить, что математика предлагает нам способы, позволяющие по матрицам парных сравнений судить о степени однородности рассматриваемого массива респондентов [Пригарина, Чеботарев, 1989]. Мы этим вопросом заниматься не будем, поскольку он выходит за пределы собственно метода ПС (решение вопроса однородности — это еще одна из причин, которая привела к расширению идей, предложенных Терстоуном).
Вспомним, что основным объектом изучения в математической статистике являются случайные величины—признаки, относительно каждого значения которых определена вероятность его встречаемости. Задать случайную величину — значит задать распределение вероятностей и наоборот. Можно сказать, что для каждого шкалируемого нами объекта о. определена некоторая случайная величина ξ., отвечающая мнению об этом объекте каждого из рассматриваемых респондентов. Эта величина нормально распределена и имеет математическое ожидание (среднее) т.и среднее квадратическое отклонение сг.
В соответствии со сказанным выше будем полагать, что нашей задачей является поиск чисел mt, т2, тп(они и будут служить искомыми оценками VpК) математических ожиданий нормально распределенных и имеющих одинаковые дисперсии at, σ2, ..., σ случайных величин ξ,, ξ2,...,ξπ,отвечающих шкалируемым объектам ανα2,..., αη. Перейдем к описанию соответствующего алгоритма.
Построение системы уравнений для искомых шкальных значений объектов
Итак, мы хотим найти средние величины (математические ожидания) некоторых гипотетически существующих случайных величин. Распределения, отвечающие этим величинам, нам неизвестны и мы вряд ли можем их найти, рассчитать экспериментально (их получение связано с тщательным изучением мнения респондента о каждом объекте, с обеспечением возможности многократного опроса одного и того же респондента и т.д. Все это вряд ли может позволить себе социолог). Значит, мы должны идти другим путем. Вспомним кое-что о понятии вероятностного распределения.
Нормальное распределение в математической статистике хорошо изучено. Это, в частности, означает, что для этого распределения существуют статистические таблицы, которые позволяют по каждому значению случайной величины найти вероятность его встречаемости, по каждой вероятности—значения, которые с этой вероятностью встречаются. Нам надо найти определенные значения наших случайных величин (те, которые являются средними). Значит, следует попытаться проанализировать, от каких вероятностей мы можем отталкиваться. Имеются ли у нас какие-либо вероятности, связанные с рассматриваемыми случайными величинами? Конечно, имеются, они заключены в наших исходных данных. Чтобы понять, как матрицы ПС могут быть связаны с некоторыми вероятностями, рассмотрим еще один элемент той модели, которая была предложена Терстоуном.
Прежде всего отметим, что, поскольку для каждого объекта совокупностям оценок разных респондентов отвечает одна и та же случайная величина, логично предположить, что приблизительное (выборочное) распределение этой величины может быть найдено двумя путями: путем многократного опроса одного (любого) респондента, либо путем однократного опроса многих респондентов. Результат будет один и тот же!
Теперь сложим все наши матрицы ПС. Нетрудно понять, что тогда на пересечении t'-й строки и у'-го столбца полученной матрицы-суммы будет стоять количество респондентов, утверждающих, что а. > а..Поделим эту сумму на общее количество респондентов и получим соответствующую долю. Обозначим ее через ρ:
Следуя описанной выше логике, позволяющей "подменять" совокупность мнений разных респондентов многократно повторенным мнением одного респондента, будем считать, что р.. говорит о том, сколь часто один респондент будет предпочитать /'-й объект у'-му (если представить себе, что мы многократно предъявляем респонденту все рассматриваемые пары объектов).
Заметим, что матрица || р.. || обладает'рядом свойств, знание которых может помочь в использовании описываемых теоретических положений на практике, а именно, для всех и jвыполняются соотношения: 0 < р.. < 1; Pjj+ р.. = \ ^ = \βусловно).
Теперь вспомним закон сравнительного суждения Терстоуна: чем чаще при многократных опросах некий респондент предпочитает объект aiобъекту д., тем дальше отстоят друг от друга отвечающие этому респонденту шкальные значения рассматриваемых объектов. Наверное, если учесть, что любому респонденту отвечает целый набор шкальных значений, каждое из которых встречается с определенной вероятностью (т.е. каждому респонденту отвечает некоторая случайная величина), то естественно предположить, что доля р.. равна вероятности того, что наша /-я случайная величина (т.е. случайная величина, отвечающая i-му объекту) больше j-vi(отвечающей j-щ объекту), или, на формальном языке:
Итак, наши эмпирические данные (суммарная матрица ПС) задают нам определенного рода вероятности. Чтобы стало ясно, каким образом можно, используя знание этих вероятностей и таблицы для нормального распределения, перейти к средним значениям случайных величин iи j(лишний раз напомним, что эти средние являются тем, что мы ищем), введем новое обозначение:
Тогда выражение для р.. перепишется в виде:
Следующие соотношения опираются на известные результаты из области математической статистики. Они не используют никакие модели восприятия, никакие предположения о сути того, что происходит в сознании одного респондента, о связи процессов, имеющих место в представлениях разных респондентов, и т.д.
Величина ξ^, будучи разностью двух нормально распределенных случайных величин ξ: и ξ. с математическими ожиданиями /и. и т.и средними квадратическими отклонениями α и σ соответственно, сама является нормально распределенной случайной величиной с математическим ожиданием т.и средним квадрати-ческим отклонением а.., определяющимися следующим образом:
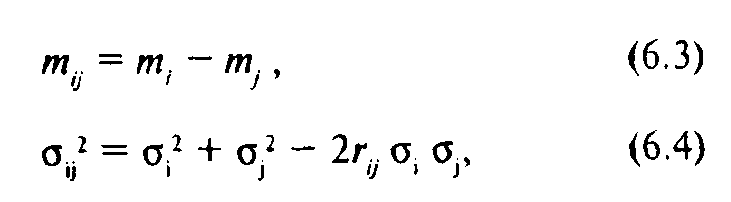
где г.. — коэффициент корреляции между ξί и ξ; (к обсуждению его "физического" смысла мы еще вернемся).
На основе соотношения (6.2) мы можем, пользуясь таблицами нормального распределения, найти отвечающее стоящей в левой части этого равенства вероятности значение величины ξ|;. Однако, чтобы это сделать, необходимы некоторые дополнительные рассуждения. Дело в том, что известные статистические таблицы разработаны только для так называемого стандартизованного нормального распределения, т.е. для таких случайных величин ξ,. , которым отвечает нулевое среднее и единичная дисперсия (конечно, нельзя рассчитать таблицы для всех мыслимых нормальных распределений, поскольку в качестве математического ожидания могут выступать любые действительные числа, в качестве дисперсии — любые положительные действительные числа). Но тем не менее таблица может все-таки быть полезной, если воспользоваться следующим известным в математической статистике положением:
Итак, пользуясь таблицей для стандартизированного нормального распределения, на основе соотношения (6.5) можно найти величину (/п.. /σί;). Обозначим ее через zir Ясно, что
что, в силу (6.3) и (6.4), эквивалентно соотношению:
Мы получили систему уравнений для нахождения искомых шкальных значений /и и /я (/ и jбыли произвольными номерами наших объектов, поэтому уравнений типа (6.6) у нас будет столько, сколько пар из этих объектов можно составить).
Подчеркнем, что уравнения (6.6) получаются на основе суммарной матрицы ПС очень быстро: по каждой частоте />.. сразу, только заглянув в соответствующую статистическую таблицу, находим г и, значит, сами уравнения. Все предыдущие рассуждения о моделях восприятия нужны только затем, чтобы оправдать этот шаг. Поэтому то, что этим рассуждениям выше уделено значительное место, не должно смущать читателя. Алгоритм практических действий пока прост. Но далее он усложняется: нам надо решить систему (6.6), а здесь есть о чем поговорить.
Решение системы уравнений
Начнем с того, что помимо интересующих нас шкальных значений изучаемых объектов, система (6.6) содержит и другие неизвестные: σ|5 σν г. Поступим с ними так, как это делали Терстоун и его последователи.
Прежде всего упростим уравнения (6.6), сделав некоторые дополнительные предположения о свойствах наших моделей, связанных с тем, каковы величины л., σ|; е.. Отметим, что в литературе известны разные способы такого упрощения. Разным ограничениям на упомянутые параметры отвечают разные модели. Именно поэтому в начале настоящего параграфа мы говорили не о модели, а о моделях Терстоуна. Опишем ту, которая приводит к наиболее простой системе уравнений.
Но прежде сделаем одно важное методологическое замечание. Вообще говоря, любые свойства используемого в социологии математического аппарата так или иначе "выходят" на определенные содержательные представления (ср. п. 3.3). Однако зачастую суть этих представлений бывает очень трудно оценить. В данном случае удается установить связь между формализмом и содержанием: проследить, какой социологический смысл имеют рассматриваемые ограничения. И просим читателя обратить внимание не только на анализируемые ниже свойства конкретной модели восприятия, но и на методологический аспект проблемы — на то, как надо связывать элементы используемого формализма с содержанием решаемой задачи.
Итак, сделаем следующие предположения.
Во-первых, предположим, что г.. = 0. Ясно, что это значительно облегчает решение системы (6.6), поскольку в правой части этой системы при таком предположении исчезает самое
"длинное" слагаемое. Но нам важно понять, какие изменения в нашу модель вносит это предположение.
Вспомним, что г — коэффициент корреляции между двумя случайными величинами: / и j. Нетрудно понять, что наличие соответствующей связи означает зависимость мнения респондента об i-м объекте от его же мнения оу'-м объекте. И наше предположение означает отрицание такой зависимости. Всегда ли это оправданно? Наверное, не всегда. Предположим, что респондент, оценивая политического лидера Иванова, учитывает свой негативный практический опыт общения с этим лидером и дает ему низкую оценку. Переходя к оценке лидера Петрова, он может также высказать отрицательное мнение просто потому, что, по его сведениям, Петров принадлежит к той же политической партии, что и Иванов. Таких примеров можно привести множество.
Приравнивая к нулю рассматриваемый коэффициент корреляции, мы тем самым налагаем и соответствующие содержательные ограничения на нашу модель. Конечно, мы далеко не всегда можем проверить, справедливы ли наши посылки. Но если мы хотим все же стремиться к получению результатов, действительно отражающих реальность, то уж во всяком случае должны по возможности давать себе отчет в том, какие модели используем.
Во-вторых, будем полагать, что σ. = Cj = σ. Другими словами, предположим, что мера уверенности в оценках нашими респондентами разных объектов одинакова. Представляется, что это предположение в большей мере сомнительно, чем сформулированное выше предположение о том, что у разных респондентов одинакова мера уверенности в оценке одного и того же объекта (собственно, последнее предположение тоже вполне может быть неадекватным реальности, но выше мы убрали соответствующую проблему, свеДя ее к требованию обеспечения определенной однородности совокупности рассматриваемых респондентов). Ради простоты формального способа поиска интересующих нас шкальных значений все же примем это предположение, но сделаем это, как и выше, "с открытыми глазами".
Итак, система (6.6) в результате сделанных допущений превращается в следующую:
В этой системе, помимо искомых величин тг т2,тп, содержится еще одно неизвестное — σ. Найти его можно только путем экспериментального изучения распределения оценок респондентом какого-либо из рассматриваемых объектов. Для социолога это обычно бывает нереально. Поэтому будем полагать, что σ — произвольно. Положим его равным I, т.е. будем решать систему (6.7) как бы без него. Но при этом не будем забывать, что найденное решение, каким бы оно ни было, всегда будет таким, что разности (/я. — т)определены лишь с точностью до некоторого постоянного множителя — σ.
Это принципиальный для социолога момент. В п. 1.1 мы уже отмечали, что с подобной неоднозначностью результатов измерения он имеет дело очень часто. Числа мало пригодны для нужд социологии. И проявляется это в первую очередь именно в том, что практически никогда их не удается определить однозначно. Степень неоднозначности определяет тип шкалы. В рассматриваемом случае эта степень (т.е. то, что разности шкальных значений определены с точностью до постоянного множителя) говорит о том, что мы имеем дело с интервальной шкалой. Если какой-то набор чисел будет решением нашей системы, то таким же решением будет и любой другой набор чисел, получающийся из первого путем растягивания (сжатия) всех интервалов между ними в одно и то же число раз.
Итак, положим σ = 1 и перейдем к обсуждению решения системы (6.7).
Нашей целью не является обучение читателя решению подобного рода систем уравнений. Тем не менее позволим себе сделать некоторые замечания по поводу такого решения, поскольку, на наш взгляд, в соответствующем подходе содержится ряд положений, имеющих определенную методическую ценность для решения многих социологических задач.
Во-первых, рассматриваемая система переопределена — число уравнений, вообще говоря, гораздо больше числа неизвестных (количество пар, которые мы можем составить из каких-либо объектов, больше, чем количество объектов, если мы имеем дело с более чем тремя объектами). Следовательно, эта система чаще всего не будет иметь решения: даже если мы и найдем решение нескольких уравнений, совсем необязательно они будут удовлетворять и оставшимся уравнениям. Как же быть? На помощь приходит знакомый нам по регрессионному анализу метод наименьших квадратов (напомним, что там мы ищем прямую линию, которая была бы максимально близка одновременно ко всем рассматриваемым точкам, может быть даже не проходя ни через одну из них). Найдем с его помощью такое решение, которое в максимальной степени будет делать схожими правые и левые части наших уравнений, может быть даже не удовлетворяя полностью ни одному из них.
Говоря более конкретно, будем искать такие т.и т,которые обращают в минимум сумму квадратов разностей между правыми и левыми частями системы (6.7):
Напомним читателю, что выбираются такие т1и mjс помощью вычисления производных выражения (6.8) (ппроизводных — по числу искомых величин) и приравнивания каждой из них к нулю. Получаем η линейных уравнений с η неизвестными. Такая система легко решается.
(Мы столь подробно говорим о способе решения системы (6.7) для того, чтобы читатель лишний раз убедился в значимости для социолога знания метода наименьших квадратов (из-за сложности построения моделей социальных явлений социолог, как правило, имеет дело с соотношениями, которые не могут быть удовлетворены в точности) и владения элементами дифференциального и интегрального исчисления. Аналогичное утверждение относительно теории вероятностей и математической статистики подтверждается текстом, изложенным в настоящем параграфе выше.)
6.2.2. BTL-моделипарныхсравнений
Цель настоящего параграфа — показать, что приведенный выше способ построения оценочной шкалы на базе первичной информации, представленной в виде матриц ПС, не является единственно возможным. Существуют и другие подходы к пониманию того, как и почему исходные матрицы из 0 и 1 могут быть связаны с искомыми шкальными значениями изучаемых объектов (здесь мы снова имеем дело с той неоднозначностью математических моделей, о которой говорили в п. 3.3).
Очень кратко опишем еще один метод ПС, называемый обычно по первым буквам фамилий известных ученых, разработавших его: Bradley R.A., Terry Μ.Ε., Luce R.D. Модели парных сравнений, предложенные этими учеными, или BTL-модели, используются, может быть, даже более часто, чем описанные выше модели Терстоуна. Краткость описания нами BTL-моделей обусловлена не тем, что они не заслуживают более пространного рассмотрения, а тем, что мы говорим о них с единственной целью — показать, что описанная выше модель Терстоуна — не единственно возможный подход к определению довольно естественным образом связи между матрицами ПС и искомыми шкальными значениями изучаемых объектов.
Воспользуемся обозначениями из [Суппес, Зинес, 1967]. Пусть а, Ь, с,...шкалируемые объекты, а К, Уь, К, ... — их шкальные оценки (искомые шкальные значения). Вместо обозначения ру будем использовать обозначение раЬ.
Предположим, что упомянутая связь детерминируется следующими соотношениями:
Ясно, что таких равенств столько, сколько пар мы можем составить из наших объектов. Они образуют систему уравнений, в которой известными величинами являются раЬ, а неизвестными — Va и Vh(аи b"пробегают" все "имена" наших объектов). Смысл этих уравнений представляется очевидным: доля людей, предпочитающих объект а объекту Ь, пропорциональна доле шкального значения а в сумме шкальных значений а и Ь. Если ни один человек не сказал, что а лучше Ь, то К = 0 и Vh=1, а если, напротив, все респонденты считают, что а лучше Ь, то К = 1 и Vh= 0.
Чтобы наша система имела решение и для составляющих его шкальных значений был гарантирован по крайней мере интервальный уровень измерения, необходимо ввести дополнительные предположения о характере исходных данных. Это ограничение по существу является неким ослаблением отношения транзитивности
[Суппес, Зинес, 1967, с. 73]
В заключение отметим, что органичность рассмотренного подхода к построению оценочной шкалы косвенно подтверждается тем, что отвечающие соответствующей модели восприятия соотношения иногда естественным образом "возникают" при решении задач иного рода. Примером может служить работа [Сатаров, Тихомирова, 1991], в которой анализировались предпочтения между парами значений рассматриваемых признаков. Для краткого пояснения с помощью примера, о чем именно идет речь, заметим, что объектом изучения служили нефтяники-вахтовики. Выяснялось, что они предпочитают: сравнительно быстро получить квартиру, но иметь меньшую зарплату или же большую зарплату, но более дальний срок получения квартиры, и т.д.
Ясно, что задачи такого рода актуальны для социологии и то, что их решение приводит к рассмотрению BTL-моделей, говорит в пользу последних.
1 2 3 4 5 6 7 8 9 ... 14